יישום תהליך הריבוי הטהור. תהליך רבייה טהור. תהליכי רבייה ומוות
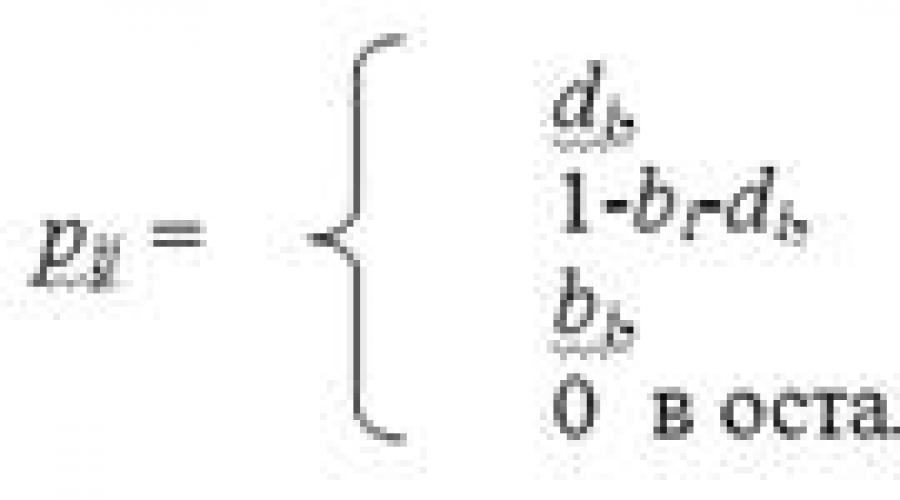
מבוא
בעבודה זו, נשקול תכנית של שרשראות מרקוב מתמשכות - מה שנקרא "תכנית מוות ורבייה"
תהליך ההתרבות והמוות הוא תהליך אקראי עם קבוצה ניתנת לספירה (סופית או אינסופית) של מצבים, המתרחשים בזמן בדיד או מתמשך. היא מורכבת מהעובדה שמערכת מסוימת ברגעים אקראיים בזמן עוברת ממצב אחד לאחר, ומעברים בין מצבים מתרחשים בפתאומיות כאשר מתרחשים אירועים מסוימים. ככלל, אירועים אלה הם משני סוגים: אחד מהם נקרא בדרך כלל לידתו של חפץ כלשהו, והשני הוא מותו של חפץ זה.
נושא זה רלוונטי ביותר בשל חשיבותם הגבוהה של תהליכי מרקוב בחקר תהליכים כלכליים, סביבתיים וביולוגיים בנוסף, תהליכי מרקוב עומדים בבסיס תורת התור, הנמצאת כיום בשימוש פעיל בתחומים כלכליים שונים, לרבות ניהול תהליכים ארגוניים.
תהליכי מרקוב של מוות ורבייה נמצאים בשימוש נרחב בהסבר תהליכים שונים המתרחשים בפיזיקה, בביוספרה, במערכת האקולוגית וכו'. יש לציין שסוג זה של תהליכי מרקוב קיבל את שמו בדיוק בגלל השימוש הנרחב שלו בביולוגיה, במיוחד במודלים של מוות ורבייה של פרטים מאוכלוסיות שונות.
בעבודה זו תוגדר משימה שמטרתה לקבוע את הציפייה המתמטית לכמה תהליכי רבייה ומוות. יינתנו דוגמאות לחישובים של מספר הבקשות הממוצע במערכת במצב נייח ויערכו הערכות למקרים שונים של תהליכי רבייה ומוות.
תהליכי רבייה ומוות
תהליכי רבייה ומוות הם מקרה מיוחד של תהליכים אקראיים של מרקוב, אשר בכל זאת מוצאים יישום רחב מאוד בחקר מערכות בדידות בעלות אופי סטוכסטי של תפקוד. תהליך ההתרבות והמוות הוא תהליך אקראי של מרקוב שבו מעברים ממצב E i מותרים רק למצבים שכנים E i-1, E i ו-E i+1. תהליך הרבייה והמוות הוא מודל הולם לתיאור שינויים המתרחשים בנפח האוכלוסיות הביולוגיות. לפי מודל זה, נאמר כי תהליך נמצא במצב E i אם גודל האוכלוסייה שווה לאברי i. במקרה זה, המעבר ממצב E i למצב E i+1 מתאים ללידה, והמעבר מ-E i ל-E i-1 מתאים למוות, ההנחה היא שנפח האוכלוסייה יכול להשתנות לא יותר מ אחד; משמעות הדבר היא כי מספר לידות ו/או מקרי מוות מרובות אינן מותרות לתהליכי רבייה ומוות.
תהליכים דיסקרטיים של רבייה ומוות פחות מעניינים מתהליכים מתמשכים, ולכן לא נדון בהם בהרחבה בהמשך ועיקר תשומת הלב מוקדשת לתהליכים מתמשכים. עם זאת, יש לציין כי עבור תהליכים בדידים מתקיימים חישובים כמעט מקבילים. המעבר של תהליך הרבייה והמוות ממצב E i חזרה למצב E i הוא עניין ישיר רק עבור רשתות מרקוב בדידות; במקרה הרציף, העוצמה שבה התהליך חוזר אליה מצב נוכחי, שווה לאינסוף, והאינסוף הזה בוטל ומוגדר באופן הבא:
במקרה של תהליך רבייה ומוות עם זמן דיסקרטי, ההסתברויות למעברים בין מדינות

כאן d i היא ההסתברות שבשלב הבא (מבחינת האוכלוסייה הביולוגית) יתרחש מוות אחד, שיפחית את נפח האוכלוסייה ל, ובלבד שבשלב זה נפח האוכלוסייה שווה ל-i. באופן דומה, b i היא ההסתברות ללידה בשלב הבא, המובילה לגידול בנפח האוכלוסייה ל; מייצג את ההסתברות שאף אחד מהאירועים הללו לא יתרחש וגודל האוכלוסייה לא ישתנה בשלב הבא. רק שלוש האפשרויות הללו מותרות. ברור שכן, כיוון שמוות לא יכול להתרחש אם אין מי ימות.
עם זאת, בניגוד לאינטואיציה, ההנחה היא כי, אשר תואמת את האפשרות של לידה כאשר אין חבר אחד באוכלוסייה. למרות שניתן לראות בכך לידה ספונטנית או יצירה אלוהית, בתורת המערכות הבדידות מודל כזה הוא הנחה משמעותית לחלוטין. כלומר, המודל הוא כזה: האוכלוסייה מייצגת זרימה של דרישות במערכת, מוות פירושו יציאה של דרישה מהמערכת, ולידה מתאימה לכניסה של דרישה חדשה למערכת. ברור שבמודל כזה בהחלט אפשרי לדרישה חדשה (לידה) להיכנס למערכת חינמית. מטריצת הסתברות מעבר עבור תהליך כללילרבייה ולמוות יש את הצורה הבאה:

אם שרשרת מרקוב היא סופית, אז השורה האחרונה של המטריצה כתובה בצורה; זה מתאים לכך שאסור להתרבות לאחר שהאוכלוסייה מגיעה לגודלה המקסימלי n. המטריצה T מכילה אפס איברים רק באלכסון הראשי ובשני האלכסונים הקרובים אליו. בגלל צורה מסוימת זו של המטריצה T, טבעי לצפות שניתוח תהליך ההתרבות והמוות לא יגרום לקשיים. בהמשך, נשקול רק תהליכים מתמשכים של רבייה ומוות, שבהם מעברים ממצב E i אפשריים רק למצבים השכנים E i-1 (מוות) ו-E i+1 (לידה). הבה נסמן ב-i את עוצמת הרבייה; הוא מתאר את הקצב שבו מתרחשת רבייה באוכלוסייה בעלת נפח i. באופן דומה, ב-i אנו מציינים את עוצמת המוות, המציינת את הקצב שבו מוות מתרחש באוכלוסייה בעלת נפח i. שימו לב שהעוצמות המוכנסות של רבייה ומוות אינן תלויות בזמן, אלא תלויות רק במצב E i, לכן, אנו מקבלים שרשרת מרקוב הומוגנית רציפה מסוג רבייה ומוות. סימונים מיוחדים אלה מוצגים מכיוון שהם מובילים ישירות לסימונים שאומצו בתורת המערכות הבדידות. בהתאם לסימון שהוצג קודם לכן יש לנו:
i = q i,i+1 ו-i = q i,i-1.
הדרישה לפיה מעברים רק למדינות השכנות הקרובות ביותר יהיו קבילים פירושה כי בהתבסס על העובדה
נקבל q ii =-(i + i). לפיכך, מטריצת עוצמת המעבר של התהליך ההומוגני הכללי של רבייה ומוות לובשת את הצורה:

שימו לב, למעט האלכסון הראשי והאלכסונים הסמוכים לו מתחת ולמעלה, כל מרכיבי המטריצה שווים לאפס. הגרף המתאים של עוצמות המעבר מוצג באיור המקביל (2.1):
איור 2.1 - גרף עוצמות מעבר לתהליך רבייה ומוות
הגדרה מדויקת יותר של תהליך מתמשך של רבייה ומוות היא כדלקמן: תהליך כלשהו הוא תהליך של רבייה ומוות אם מדובר בשרשרת מרקוב הומוגנית עם מצבים רבים (E 0, E 1, E 2, ...), אם לידה ומוות הם אירועים עצמאיים (הדבר נובע ישירות מנכס מרקוב) ואם מתקיימים התנאים הבאים:
(בדיוק לידה אחת במרווח הזמן (t,t+Dt), גודל האוכלוסייה הוא i) ;
(בדיוק 1 מוות במרווח הזמן (t,t+Dt) | נפח אוכלוסיה שווה ל-i);
= (בדיוק 0 לידות במרווח הזמן (t,t+Dt) | גודל האוכלוסייה הוא i);
= (בדיוק 0 מקרי מוות במרווח הזמן (t,t+Dt) | נפח אוכלוסיה שווה ל-i).
לפיכך, ?t, עד דיוק, היא ההסתברות להולדת פרט חדש באוכלוסייה של n פרטים, והיא ההסתברות למותו של פרט באוכלוסייה זו בזמן.
הסתברויות המעבר מספקות את משוואות קולמוגורוב ההפוכות. לפיכך, ההסתברות שתהליך מתמשך של רבייה ומוות בזמן t נמצא במצב E i (נפח האוכלוסייה שווה ל-i) מוגדרת כ(2.1):

כדי לפתור את המערכת המתקבלת של משוואות דיפרנציאליות במקרה הלא נייח, כאשר ההסתברויות P i (t), i=0,1,2,..., תלויות בזמן, יש צורך לציין את התפלגות ההסתברויות הראשוניות P i (0), i=0,1,2 ,…, ב-t=0. בנוסף, יש לעמוד בתנאי הנורמליזציה.
הבה נבחן כעת את התהליך הפשוט ביותר של רבייה טהורה, המוגדר כתהליך שעבורו i = 0 עבור כל ה-i. בנוסף, כדי לפשט את הבעיה עוד יותר, נניח ש-i = עבור כל i=0,1,2,... . החלפת ערכים אלו במשוואות (2.1) נקבל (2.2):

לשם הפשטות, אנו גם מניחים שהתהליך מתחיל ברגע אפס עם אפס איברים, כלומר:
מכאן נקבל את הפתרון עבור P 0 (t):
החלפת פתרון זה במשוואה (2.2) עבור i = 1, נגיע למשוואה:
הפתרון למשוואה דיפרנציאלית זו יש כמובן את הצורה:
זו התפלגות הפואסון המוכרת. לפיכך, תהליך של רבייה טהורה בקצב קבוע מביא לרצף לידות היוצר זרימת פואסון.
העניין הגדול ביותר במונחים מעשיים הוא ההסתברויות של מצבי תהליך ההתרבות והמוות במצב יציב. בהנחה שלתהליך יש את התכונה הארגודית, כלומר יש גבולות
נעבור לקביעת ההסתברויות המגבילות P i. ניתן לקבל משוואות לקביעת ההסתברויות של משטר נייח ישירות מ-(2.1), תוך התחשבות בכך ש-dP i (t)/dt = 0 ב:
מערכת המשוואות המתקבלת נפתרת תוך התחשבות בתנאי הנורמליזציה (2.4):
ניתן להרכיב את מערכת המשוואות (2.3) למצב היציב של תהליך הרבייה והמוות ישירות מגרף עוצמות המעבר באיור 2.1, תוך יישום העיקרון של שוויון זרימות ההסתברות על מצבים בודדים של התהליך. לדוגמה, אם ניקח בחשבון את המצב של E i במצב יציב, אז:
עוצמת זרימת ההסתברויות ב- ו
עוצמת זרימת ההסתברויות מ.
בשיווי משקל, שתי הזרימות הללו חייבות להיות שוות, ולכן אנו מקבלים ישירות:
אבל זה בדיוק השוויון הראשון במערכת (2.3). באופן דומה, אנו יכולים להשיג את השוויון השני של המערכת. ניתן ליישם את אותם טיעוני שימור זרימה שניתנו קודם לכן על זרימת ההסתברויות על פני כל גבול סגור. לדוגמה, במקום לבחור כל מצב וליצור עבורו משוואה, ניתן לבחור רצף של קווי מתאר, שהראשון שבהם מכסה את המצב E 0, השני - המצב E 0 ו-E 1, וכן הלאה, בכל פעם. כולל המדינה הבאה בגבול חדש. ואז עבור המעגל ה-i (מצב המקיף E 0, E 1,..., E i-1), ניתן לכתוב את התנאי לשמירה על זרימת ההסתברויות בצורה הפשוטה הבאה:
ניתן לנסח שוויון (2.5) ככלל: עבור המערכת הפשוטה ביותר של רבייה ומוות, שהיא במצב נייח, ההסתברות לזרימות בין כל שני מצבים שכנים שווה.
מערכת המשוואות המתקבלת מקבילה למערכת שנגזרה קודם לכן. כדי להרכיב את מערכת המשוואות האחרונה, עליך לצייר קו אנכי המחלק מדינות שכנות ולהשוות את הזרימות על פני הגבול המתקבל.
את הפתרון למערכת (2.5) ניתן למצוא באינדוקציה מתמטית.
עבור i=1 יש לנו
צורת השוויון שהתקבלה מראה שלפתרון הכללי של מערכת המשוואות (2.5) יש את הצורה:
או, בהינתן שבהגדרה, המוצר מעל סט ריק שווה לאחד:
לפיכך, כל ההסתברויות P i למצב יציב באות לידי ביטוי באמצעות קבוע לא ידוע בודד P 0 . שוויון (2.4) נותן תנאי נוסף המאפשר לנו לקבוע P 0 . לאחר מכן, בסיכומו של כל ה-i, עבור P 0 נקבל (2.7):

הבה נפנה לשאלת קיומן של הסתברויות נייחות Pi. על מנת שהביטויים המתקבלים יציינו הסתברויות, בדרך כלל מוטלת הדרישה ש- P 0 >0. זה כמובן מטיל הגבלה על מקדמי הרבייה והמוות במשוואות המתאימות. בעיקרו של דבר זה דורש מהמערכת להתרוקן מדי פעם; מצב זה של יציבות נראה הגיוני מאוד אם נסתכל על דוגמאות החיים האמיתיים. אם הם גדלים מהר מדי בהשוואה, אז עשוי להתברר שעם הסתברות חיובית ברגע האחרון של הזמן t התהליך ישאיר את מרחב הפאזה (0,1,...) ל"נקודה באינסוף?" (יהיו יותר מדי פרטים באוכלוסייה). במילים אחרות, התהליך יהפוך לבלתי סדיר, ואז ייפגע השוויון (2.4). הבה נגדיר את שני הסכומים הבאים:

לסדירות תהליך ההתרבות והמוות, יש צורך ומספיק ש-S 2 =.
לקיום התפוצה הנייחת שלו יש צורך ומספיק ש-S 1< .
על מנת שכל המצבים E i בתהליך הנחשב של רבייה ומוות יהיו ארגודיים, זה הכרחי ומספיק להתכנסות של הסדרה S 1< , при этом ряд должен расходиться S 2 = . Только эргодический случай приводит к установившимся вероятностям P i , i = 0, 1, 2, …, и именно этот случай представляет интерес. Заметим, что условия эргодичности выполняются, например, когда, начиная с некоторого i, все члены последовательности {} ограничены единицей, т. е. тогда, когда существует некоторое i 0 (и некоторое С<1) такое, что для всех ii 0 выполняется неравенство:
ניתן לתת לאי-שוויון זה פרשנות פשוטה: החל ממצב מסוים E i ולכל המצבים הבאים, עוצמת זרימת ההתרבות חייבת להיות פחותה מעוצמת זרימת המוות.
לפעמים בפועל יש תהליכים של רבייה "טהורה". תהליך הרבייה ה"טהורה" הוא תהליך של מוות ורבייה שבו עוצמת כל זרימות המוות שווה לאפס. גרף המצב של תהליך כזה ללא הגבלות על מספר המצבים מוצג באיור (2.2):

איור 2.2 - גרף של עוצמות מעבר לתהליך של רבייה "טהורה".
המושג של מוות "טהור" מוצג באופן דומה. תהליך המוות ה"טהור" הוא תהליך של מוות ורבייה שבו העוצמות של כל זרימות הרבייה שוות לאפס. גרף המצב של תהליך כזה ללא הגבלות על מספר המדינות מוצג באיור:

איור 2.3 - גרף של עוצמות מעבר לתהליך של מוות "טהור".
ניתן לקבל את מערכת המשוואות קולמוגורוב לתהליכים כאלה ממערכת המשוואות (2.1), שבה יש צורך להגדיר את כל עוצמות הזרימה של תהליכי מוות שווה לאפס: .
ההכללה הפשוטה ביותר של תהליך פואסון מתקבלת בהנחה שההסתברויות לקפיצות יכולות להיות תלויות במצב הנוכחי של המערכת. זה מביא אותנו לדרישות הבאות.
פוסטולציות. (i) מעבר ישיר מהמצב אפשרי רק למצב . ואילו ההסתברות (המותנית) ליותר מקפיצה אחת במרווח זה היא .
המאפיין הייחודי של הנחה זו הוא שהזמן שהמערכת מבלה בכל מצב מסוים אינו משחק תפקיד; שינויים פתאומיים במצב אפשריים, אבל כל עוד המערכת נשארת באותו מצב, היא לא מזדקנת.
תן שוב להיות ההסתברות שבזמן שהמערכת נמצאת במצב. פונקציות אלו מספקות מערכת של משוואות דיפרנציאליות, שניתן לגזור באמצעות הארגומנטים של הפסקה הקודמת עם השינוי היחיד ש-(5) בפסקה הקודמת מוחלף ב-
לפיכך, אנו מקבלים את המערכת הבסיסית של משוואות דיפרנציאליות
 (2)
(2)
בתהליך פואסון, היה טבעי להניח שבזמן 0 המערכת עוזבת את המצב ההתחלתי. כעת אנו יכולים לאפשר מקרה כללי יותר שבו המערכת עוזבת מצב ראשוני שרירותי. ואז נקבל את זה
תנאים ראשוניים אלה קובעים באופן ייחודי את הפתרון של מערכת (2). (באופן מיוחד, ). נוסחאות מפורשות עבור נגזרו באופן עצמאי על ידי מחברים רבים, אך הן אינן מעניינות אותנו.
דוגמא. ריקבון רדיואקטיבי. כתוצאה מפליטת חלקיקים או קרניים, אטום רדיואקטיבי, נניח אורניום, יכול להפוך לאטום מסוג אחר. כל סוג מייצג מצב אפשרי, וככל שהתהליך מתקדם אנו מקבלים רצף של מעברים. לפי תיאוריות פיזיקליות מקובלות, הסתברות המעבר נשארת ללא שינוי בזמן שהאטום במצב, והשערה זו באה לידי ביטוי בהנחה הראשונית שלנו. לכן, תהליך זה מתואר על ידי משוואות דיפרנציאליות (2) (עובדה ידועה היטב לפיזיקאים). אם הוא מצב סופי שממנו לא אפשריים מעברים אחרים, מערכת (2) מסתיימת ב-. (כאשר אנו מקבלים אוטומטית).
משרד החינוך של הרפובליקה של בלארוס
מוסד חינוכי
"אוניברסיטת גומל סטייט
על שם פרנסיסק סקארינה"
הפקולטה למתמטיקה
המחלקה לקיברנטיקה כלכלית ותורת ההסתברות
פרויקט הקורס
מאפיינים נייחים של תהליכי רבייה ומוות
מוציא להורג:
בוכובט ויקטוריה
אלכסנדרובנה
יועץ מדעי:
ראש המחלקה,
מלינקובסקי יורי
ולדימירוביץ'
גומל 2011
מבוא
תהליכי רבייה ומוות
דוגמאות לתהליכי רבייה ומוות במקרה של מערכות התורים הפשוטות ביותר
3 קביעת תוחלת מתמטית למערכת התורים M/M/n
4 קביעת התוחלת המתמטית למערכת התורים M/M/n/N
קביעת הציפייה המתמטית לכמה תהליכים של רבייה ומוות
2 תהליך רבייה ומוות עם עוצמת הלידה הגוברת באופן ליניארי ועוצמת המוות הגדלה ריבועית
4 זרם נוסף ומספר אינסופי של מכשירים
5 מערכת עם הגבלה על משך השהייה של הבקשה
6 מערכת עם הגבלה על זמן השהייה של בקשה, זרימה נוספת ומספר אינסופי של מכשירים
סיכום
ציפייה בתור
מבוא
בעבודה זו, נשקול תכנית של שרשראות מרקוב מתמשכות - מה שנקרא "תכנית מוות ורבייה"
תהליך ההתרבות והמוות הוא תהליך אקראי עם קבוצה ניתנת לספירה (סופית או אינסופית) של מצבים, המתרחשים בזמן בדיד או מתמשך. היא מורכבת מהעובדה שמערכת מסוימת ברגעים אקראיים בזמן עוברת ממצב אחד לאחר, ומעברים בין מצבים מתרחשים בפתאומיות כאשר מתרחשים אירועים מסוימים. ככלל, אירועים אלה הם משני סוגים: אחד מהם נקרא בדרך כלל לידתו של חפץ כלשהו, והשני הוא מותו של חפץ זה.
נושא זה רלוונטי ביותר בשל חשיבותם הגבוהה של תהליכי מרקוב בחקר תהליכים כלכליים, סביבתיים וביולוגיים בנוסף, תהליכי מרקוב עומדים בבסיס תורת התור, הנמצאת כיום בשימוש פעיל בתחומים כלכליים שונים, לרבות ניהול תהליכים ארגוניים.
תהליכי מרקוב של מוות ורבייה נמצאים בשימוש נרחב בהסבר תהליכים שונים המתרחשים בפיזיקה, בביוספרה, במערכת האקולוגית וכו'. יש לציין שסוג זה של תהליכי מרקוב קיבל את שמו בדיוק בגלל השימוש הנרחב שלו בביולוגיה, במיוחד במודלים של מוות ורבייה של פרטים מאוכלוסיות שונות.
בעבודה זו תוגדר משימה שמטרתה לקבוע את הציפייה המתמטית לכמה תהליכי רבייה ומוות. יינתנו דוגמאות לחישובים של מספר הבקשות הממוצע במערכת במצב נייח ויערכו הערכות למקרים שונים של תהליכי רבייה ומוות.
1. תהליכי רבייה ומוות
תהליכי רבייה ומוות הם מקרה מיוחד של תהליכים אקראיים של מרקוב, אשר בכל זאת מוצאים יישום רחב מאוד בחקר מערכות בדידות בעלות אופי סטוכסטי של תפקוד. תהליך הרבייה והמוות הוא תהליך אקראי של מרקוב שבו עוברים ממצב E אני תקף רק במדינות השכנות E i-1 , E אני ו-E i+1 . תהליך הרבייה והמוות הוא מודל הולם לתיאור שינויים המתרחשים בנפח האוכלוסיות הביולוגיות. לפי מודל זה, התהליך אמור להיות במצב E אני , אם גודל האוכלוסייה שווה לאברים i. במקרה זה, המעבר ממצב E אני לציין E i+1 מתאים ללידה, ומעבר מ-E אני ב-E i-1 - מוות, ההנחה היא שנפח האוכלוסייה יכול להשתנות בלא יותר מאחד; משמעות הדבר היא כי מספר לידות ו/או מקרי מוות מרובות אינן מותרות עבור תהליכי רבייה ומוות.
תהליכים דיסקרטיים של רבייה ומוות פחות מעניינים מתהליכים מתמשכים, ולכן לא נדון בהם בהרחבה בהמשך ועיקר תשומת הלב מוקדשת לתהליכים מתמשכים. עם זאת, יש לציין כי עבור תהליכים בדידים מתקיימים חישובים כמעט מקבילים. מעבר של תהליך רבייה ומוות ממצב E אני חזרה למצב ה' אני יש עניין ישיר רק עבור רשתות מרקוב דיסקרטיות; במקרה הרציף, הקצב שבו התהליך חוזר למצב הנוכחי שווה לאינסוף, והאינסוף הזה בוטל ומוגדר באופן הבא:
במקרה של תהליך רבייה ומוות עם זמן דיסקרטי, ההסתברויות למעברים בין מדינות
כאן די היא ההסתברות שבשלב הבא (במונחים של האוכלוסייה הביולוגית) יתרחש מוות אחד, שמקטין את גודל האוכלוסייה ל, ובלבד שבשלב זה גודל האוכלוסייה שווה ל-i. באופן דומה, bi היא ההסתברות ללידה בשלב הבא, המובילה לגידול בגודל האוכלוסייה ל; מייצג את ההסתברות שאף אחד מהאירועים הללו לא יתרחש וגודל האוכלוסייה לא ישתנה בשלב הבא. רק שלוש האפשרויות הללו מותרות. ברור שכן, כיוון שמוות לא יכול להתרחש אם אין מי ימות.
עם זאת, בניגוד לאינטואיציה, ההנחה היא כי, אשר תואמת את האפשרות של לידה כאשר אין חבר אחד באוכלוסייה. למרות שניתן לראות בכך לידה ספונטנית או יצירה אלוהית, בתורת המערכות הבדידות מודל כזה הוא הנחה משמעותית לחלוטין. כלומר, המודל הוא כזה: האוכלוסייה מייצגת זרימה של דרישות במערכת, מוות פירושו יציאה של דרישה מהמערכת, ולידה מתאימה לכניסה של דרישה חדשה למערכת. ברור שבמודל כזה בהחלט אפשרי לדרישה חדשה (לידה) להיכנס למערכת חינמית. למטריצת הסתברות המעבר לתהליך הכללי של רבייה ומוות יש את הצורה הבאה:
אם שרשרת מרקוב היא סופית, אז השורה האחרונה של המטריצה כתובה בצורה; זה מתאים לכך שאסור להתרבות לאחר שהאוכלוסייה מגיעה לגודלה המקסימלי n. המטריצה T מכילה אפס איברים רק באלכסון הראשי ובשני האלכסונים הקרובים אליו. בגלל צורה מסוימת זו של המטריצה T, טבעי לצפות שניתוח תהליך ההתרבות והמוות לא יגרום לקשיים. בהמשך, נשקול רק תהליכים מתמשכים של רבייה ומוות, שבהם מעברים ממצב Ei אפשריים רק למדינות השכנות Ei-1 (מוות) ו- Ei+1 (לידה). הבה נסמן את עוצמת הרבייה על ידי li; הוא מתאר את הקצב שבו מתרחשת רבייה באוכלוסייה בעלת נפח i. באופן דומה, ב-mi אנו מציינים את עוצמת המוות, המציינת את הקצב שבו מתרחש המוות באוכלוסייה בעלת נפח i. שימו לב שהעוצמות המוכנסות של רבייה ומוות אינן תלויות בזמן, אלא תלויות רק במצב אי, לכן, אנו מקבלים שרשרת מרקוב הומוגנית רציפה מסוג רבייה ומוות. סימונים מיוחדים אלה מוצגים מכיוון שהם מובילים ישירות לסימונים שאומצו בתורת המערכות הבדידות. בהתאם לסימון שהוצג קודם לכן יש לנו:
li= qi,i+1 ו-mi= qi,i-1.
הדרישה לפיה מעברים רק למדינות השכנות הקרובות ביותר יהיו קבילים פירושה כי בהתבסס על העובדה
נקבל qii=-(mi+ li). לפיכך, מטריצת עוצמת המעבר של התהליך ההומוגני הכללי של רבייה ומוות לובשת את הצורה:
שימו לב, למעט האלכסון הראשי והאלכסונים הסמוכים לו מתחת ולמעלה, כל מרכיבי המטריצה שווים לאפס. הגרף המתאים של עוצמות המעבר מוצג באיור המקביל (2.1):
איור 2.1 - גרף עוצמות מעבר לתהליך רבייה ומוות
הגדרה מדויקת יותר לתהליך מתמשך של רבייה ומוות היא כדלקמן: תהליך כלשהו הוא תהליך של רבייה ומוות אם מדובר בשרשרת מרקוב הומוגנית עם מצבים רבים (E0, E1, E2, ...), אם לידה ו מוות הם אירועים עצמאיים (זה נובע ישירות מנכס מרקוב) ואם מתקיימים התנאים הבאים:
1) (בדיוק לידה אחת במרווח הזמן (t,t+?t), גודל האוכלוסייה הוא i) ;
2) (בדיוק 1 מוות במרווח הזמן (t,t+?t) | נפח אוכלוסיה שווה ל-i);
3) = (בדיוק 0 לידות במרווח הזמן (t,t+?t)| גודל האוכלוסייה הוא i);
4) = (בדיוק 0 מקרי מוות במרווח הזמן (t,t+?t) | נפח אוכלוסיה שווה ל-i).
לפיכך, ?t, עד דיוק, היא ההסתברות להולדת פרט חדש באוכלוסייה של n פרטים, והיא ההסתברות למותו של פרט באוכלוסייה זו בזמן.
הסתברויות המעבר מספקות את משוואות קולמוגורוב ההפוכות. לפיכך, ההסתברות שתהליך מתמשך של רבייה ומוות בזמן t נמצא במצב Ei (נפח אוכלוסייה שווה ל-i) מוגדרת כ(2.1):
כדי לפתור את המערכת המתקבלת של משוואות דיפרנציאליות במקרה הלא נייח, כאשר ההסתברויות Pi(t), i=0,1,2,..., תלויות בזמן, יש צורך לציין את התפלגות ההסתברויות הראשוניות Pi(0 ), i=0,1,2,… , ב-t=0. בנוסף, יש לעמוד בתנאי הנורמליזציה.
הבה נבחן כעת את התהליך הפשוט ביותר של רבייה טהורה, המוגדר כתהליך שעבורו mi = 0 עבור כל i. בנוסף, כדי לפשט עוד יותר את הבעיה, נניח ש-li=l עבור כל i=0,1,2,... . החלפת ערכים אלו במשוואות (2.1) נקבל (2.2):
לשם הפשטות, אנו גם מניחים שהתהליך מתחיל ברגע אפס עם אפס איברים, כלומר:
מכאן נקבל את הפתרון עבור P0(t):
החלפת פתרון זה במשוואה (2.2) עבור i = 1, נגיע למשוואה:
הפתרון למשוואה דיפרנציאלית זו יש כמובן את הצורה:
זו התפלגות הפואסון המוכרת. לפיכך, תהליך של רבייה טהורה בעוצמה קבועה l מוביל לרצף של לידות היוצרות זרימת פואסון.
העניין הגדול ביותר במונחים מעשיים הוא ההסתברויות של מצבי תהליך ההתרבות והמוות במצב יציב. בהנחה שלתהליך יש את התכונה הארגודית, כלומר יש גבולות
הבה נעבור לקביעת ההסתברויות המגבילות Pi. ניתן לקבל משוואות לקביעת ההסתברויות של המצב הנייח ישירות מ-(2.1), תוך התחשבות בכך ש-dPi(t)/dt = 0 ב:
מערכת המשוואות המתקבלת נפתרת תוך התחשבות בתנאי הנורמליזציה (2.4):
ניתן להרכיב את מערכת המשוואות (2.3) למצב היציב של תהליך הרבייה והמוות ישירות מגרף עוצמות המעבר באיור 2.1, תוך יישום העיקרון של שוויון זרימות ההסתברות על מצבים בודדים של התהליך. לדוגמה, אם ניקח בחשבון את המצב של אי במצב יציב, אז:
עוצמת זרימת ההסתברויות ב- ו
עוצמת זרימת ההסתברויות מ.
בשיווי משקל, שתי הזרימות הללו חייבות להיות שוות, ולכן אנו מקבלים ישירות:
אבל זה בדיוק השוויון הראשון במערכת (2.3). באופן דומה, אנו יכולים להשיג את השוויון השני של המערכת. ניתן ליישם את אותם טיעוני שימור זרימה שניתנו קודם לכן על זרימת ההסתברויות על פני כל גבול סגור. למשל, במקום לבחור כל מצב ולבנות עבורו משוואה, ניתן לבחור רצף של קווי מתאר, שהראשון מכסה את המצב E0, השני - המצב E0 ו-E1 וכן הלאה, כל פעם כולל את הבא. מדינה בגבול חדש. לאחר מכן עבור קו המתאר ה-i (מצב המקיף E0, E1,..., Ei-1), ניתן לכתוב את התנאי לשמירה על זרימת ההסתברויות בצורה הפשוטה הבאה:
ניתן לנסח שוויון (2.5) ככלל: עבור המערכת הפשוטה ביותר של רבייה ומוות, שהיא במצב נייח, ההסתברות לזרימות בין כל שני מצבים שכנים שווה.
מערכת המשוואות המתקבלת מקבילה למערכת שנגזרה קודם לכן. כדי להרכיב את מערכת המשוואות האחרונה, עליך לצייר קו אנכי המחלק מדינות שכנות ולהשוות את הזרימות על פני הגבול המתקבל.
את הפתרון למערכת (2.5) ניתן למצוא באינדוקציה מתמטית.
עבור i=1 יש לנו
צורת השוויון שהתקבלה מראה שלפתרון הכללי של מערכת המשוואות (2.5) יש את הצורה:
או, בהינתן שבהגדרה, המוצר מעל סט ריק שווה לאחד:
לפיכך, כל ההסתברויות Pi למצב היציב באות לידי ביטוי באמצעות קבוע P0 יחיד לא ידוע. שוויון (2.4) נותן תנאי נוסף המאפשר לנו לקבוע P0. ואז, בסיכומו של כל ה-i, עבור P0 נקבל (2.7):
הבה נפנה לשאלת קיומן של הסתברויות נייחות Pi. כדי שהביטויים המתקבלים יציינו הסתברויות, בדרך כלל מוטלת הדרישה ש-P0>0. זה כמובן מטיל הגבלה על מקדמי הרבייה והמוות במשוואות המתאימות. בעיקרו של דבר זה דורש מהמערכת להתרוקן מדי פעם; מצב זה של יציבות נראה הגיוני למדי אם נסתכל על דוגמאות מהחיים האמיתיים. אם הם גדלים מהר מדי בהשוואה, אז עשוי להתברר שעם הסתברות חיובית ברגע האחרון של הזמן t התהליך ישאיר את מרחב הפאזה (0,1,...) ל"נקודה באינסוף?" (יהיו יותר מדי פרטים באוכלוסייה). במילים אחרות, התהליך יהפוך לבלתי סדיר, ואז ייפגע השוויון (2.4). הבה נגדיר את שני הסכומים הבאים:
לסדירות תהליך ההתרבות והמוות, יש צורך ומספיק ש-S2 = .
לקיום התפוצה הנייחת שלו יש צורך ומספיק ש-S1< .
כדי שכל המצבים Ei של תהליך ההתרבות והמוות הנחשב יהיו ארגודיים, יש צורך ומספיק שהסדרה S1 תתכנס< , при этом ряд должен расходиться S2 = . Только эргодический случай приводит к установившимся вероятностям Pi, i = 0, 1, 2, …, и именно этот случай представляет интерес. Заметим, что условия эргодичности выполняются, например, когда, начиная с некоторого i, все члены последовательности {} ограничены единицей, т. е. тогда, когда существует некоторое i0 (и некоторое С<1) такое, что для всех ii0 выполняется неравенство:
לאי-שוויון זה ניתן לתת פרשנות פשוטה: החל ממצב מסוים Ei ולכל המצבים הבאים, עוצמת זרימת ההתרבות חייבת להיות פחותה מעוצמת זרימת המוות.
לפעמים בפועל יש תהליכים של רבייה "טהורה". תהליך הרבייה ה"טהורה" הוא תהליך של מוות ורבייה שבו עוצמת כל זרימות המוות שווה לאפס. גרף המצב של תהליך כזה ללא הגבלות על מספר המצבים מוצג באיור (2.2):
איור 2.2 - גרף של עוצמות מעבר לתהליך של רבייה "טהורה".
המושג של מוות "טהור" מוצג באופן דומה. תהליך המוות ה"טהור" הוא תהליך של מוות ורבייה שבו העוצמות של כל זרימות הרבייה שוות לאפס. גרף המצב של תהליך כזה ללא הגבלות על מספר המדינות מוצג באיור:
איור 2.3 - גרף של עוצמות מעבר לתהליך של מוות "טהור".
ניתן לקבל את מערכת המשוואות קולמוגורוב לתהליכים כאלה ממערכת המשוואות (2.1), שבה יש צורך להגדיר את כל עוצמות הזרימה של תהליכי מוות שווה לאפס: .
2. דוגמאות לתהליכי ריבוי ומוות במקרה של מערכות התורים הפשוטות ביותר
1 קביעת הציפייה המתמטית למערכת התורים M/M/1
מערכת התורים הנבחנת היא תהליך של רבייה ומוות עם גרף המעבר הבא (איור 3.1):
איור 3.1 - גרף של עוצמות מעבר עבור מערכת M/M/1
מתנאי הארגודיות לתהליך המוות והרבייה עולה כי אם, אז ישנה התפלגות נייחת ייחודית החופפת לזו הארגודית, הנקראת מקדם העומס ברשת. למשוואת שיווי המשקל יש את הצורה, שממנה אנו מוצאים כי:
ניתן למצוא את ההסתברות באמצעות תנאי הנורמליזציה (2.4), המרמז על כך ולכן
כלומר, למספר הבקשות במערכת תור כזו במצב נייח יש התפלגות גיאומטרית.
קל למצוא את פונקציית ההפקה של התפלגות כזו:
מכאן נקבל ביטוי למספר האפליקציות הממוצע במערכת במצב נייח:
ניכר כי התור במערכת התורים גדל ללא הגבלה.
2 קביעת תוחלת מתמטית למערכת התורים M/M/n/0
זוהי מערכת ללא הפסדים ללא המתנה. אם בקשה נכנסת למערכת בזמן שכל n הקווים עסוקים בשירות, אזי היא אובדת. מערכת כזו הוצגה על ידי המהנדס הדני ארלנג בתחילת המאה הקודמת ושימשה כמודל לעיבוד שיחות הנכנסות למרכזית טלפון. גרף המעבר עבור מערכת תורים כזו נראה כך (איור 3.2):
איור 3.2 - גרף של עוצמות מעבר עבור מערכת M/M/n/0
מכיוון שמספר המצבים של המערכת הוא סופי ושרשרת מרקוב אינה ניתנת לצמצום, ההתפלגות הנייחת היחידה החופפת לזו הארגודית קיימת תמיד עבור כל פרמטר.
מכאן נקבל:
את ההסתברות, כמו תמיד, ניתן למצוא מתנאי הנורמליזציה (2.4), שממנו:
כך אנו מקבלים:
המספר הממוצע של יישומים במערכת נקבע על פי היחס:
עבור n גדול, ניתן להשתמש באסימפטוטיקה.
2.3 קביעת תוחלת מתמטית למערכת התורים M/M/n
זוהי מערכת המתנה רב-קו. אם כל n הקווים עסוקים בבקשות שירות, אזי עוצמת השירות שווה. גרף המעבר עבור מערכת זו נראה כך (איור 3.3):
איור 3.3 - גרף של עוצמות מעבר עבור מערכת M/M/n
קיימת התפלגות נייחת אם
למשוואות שיווי המשקל יש את הצורה הבאה:
מכאן, בדומה למקרה הקודם, אנו מקבלים
מצב הנורמליזציה במקרה זה יקבל את הצורה:
מאיפה זה נובע מכך
המספר הממוצע של יישומים במצב נייח הוא
2.4 קביעת הציפייה המתמטית למערכת התורים M/M/n/N
מדובר במערכת רב מסלולית עם מספר מצומצם של אזורי המתנה. היא שונה ממערכת התורים הקודמת בכך שיש לה רק N מקומות המתנה. לכן, גרף המעבר במקרה זה נראה כך (איור 3.4):
איור 3.4 - גרף של עוצמות מעבר עבור מערכת M/M/n/N
מכיוון שמספר המצבים של המערכת הוא סופי, תמיד קיימת התפלגות נייחת יחידה עבור כל פרמטר. משוואות שיווי המשקל לובשות את הצורה:
מכאן נובע שההסתברויות הנייחות הן בעלות צורה זהה למערכת התורים הקודמת, כאשר ההבדל היחיד הוא שהן מוגדרות עבורן. לכן
ההסתברות נקבעת מתנאי הנורמליזציה (2.4):
איפה אנחנו מקבלים:
המספר הממוצע של יישומים במערכת נקבע על פי היחס:
3. קביעת הציפייה המתמטית לכמה תהליכים של רבייה ומוות
1 תהליך רבייה ומוות עם עצימות הולכת וגוברת ליניארית של לידה ומוות
איור 1 - גרף של עוצמות מעבר למקרה הראשון של תהליך רבייה ומוות
הבה נכתוב את משוואות שיווי המשקל עבור הסתברויות נייחות של מצבים:
כדי לקבוע את הציפייה המתמטית, אנו משתמשים בנוסחה הבאה:
היכן נקבע על ידי הנוסחה.
לפיכך, המספר הממוצע של יישומים במערכת במצב נייח שווה ל:
3.2 תהליך רבייה ומוות עם שיעור ילודה עולה באופן ליניארי ושיעור מוות עולה ריבועית
תנו לקצב li שבו מתרחשת רבייה באוכלוסיה של נפח i, ועוצמת המוות mi, המציינת את הקצב שבו מתרחש המוות באוכלוסייה בנפח i, נקבעים על ידי הכלל הבא:
לגרף עוצמות המעבר עבור תהליך נתון של רבייה ומוות יש את הצורה:
איור 2 - גרף של עוצמות מעבר למקרה השני של תהליך רבייה ומוות
הבה נכתוב את משוואות שיווי המשקל עבור הסתברויות נייחות של מצבים:
3 תהליך רבייה ומוות עם עוצמת הלידה הגוברת באופן ליניארי ועוצמת המוות הגדלה ריבועית
תנו לקצב li שבו מתרחשת רבייה באוכלוסיה של נפח i, ועוצמת המוות mi, המציינת את הקצב שבו מתרחש המוות באוכלוסייה בנפח i, נקבעים על ידי הכלל הבא:
לגרף עוצמות המעבר עבור תהליך נתון של רבייה ומוות יש את הצורה
איור 3 - גרף עוצמות המעבר למקרה השלישי של תהליך רבייה ומוות
הבה נכתוב את משוואות שיווי המשקל עבור הסתברויות נייחות של מצבים:
כדי למצוא את הציפייה המתמטית, אנו משתמשים בנוסחה. אנו מוצאים שהמספר הממוצע של יישומים במערכת במצב נייח שווה ל:
3.4 זרימה נוספת ומספר אינסופי של מכשירים
תנו לקצב li שבו מתרחשת רבייה באוכלוסיה של נפח i, ועוצמת המוות mi, המציינת את הקצב שבו מתרחש המוות באוכלוסייה בנפח i, נקבעים על ידי הכלל הבא:
לגרף עוצמות המעבר עבור תהליך נתון של רבייה ומוות יש את הצורה:
איור 4 - גרף של עוצמות מעבר למקרה הרביעי של תהליך רבייה ומוות
הבה נכתוב את משוואות שיווי המשקל עבור הסתברויות נייחות של מצבים:
כדי למצוא את הציפייה המתמטית, אנו משתמשים בנוסחה. אנו מוצאים שהמספר הממוצע של יישומים במערכת במצב נייח שווה ל:
בוא נאמוד מלמעלה:
לכן:
3.5 מערכת עם הגבלה על משך השהות של הבקשה
תנו לקצב li שבו מתרחשת רבייה באוכלוסיה של נפח i, ועוצמת המוות mi, המציינת את הקצב שבו מתרחש המוות באוכלוסייה בנפח i, נקבעים על ידי הכלל הבא:
לגרף עוצמות המעבר עבור תהליך נתון של רבייה ומוות יש את הצורה:
איור 5 - גרף של עוצמות מעבר למקרה החמישי של תהליך רבייה ומוות
הבה נכתוב את משוואות שיווי המשקל עבור הסתברויות נייחות של מצבים:
כדי למצוא את הציפייה המתמטית, אנו משתמשים בנוסחה. אנו מוצאים שהמספר הממוצע של יישומים במערכת במצב נייח שווה ל:
בוא נאמוד מלמעלה:
לכן:
אנו משיגים את האומדן הבא עבור המספר הממוצע של יישומים במערכת במצב נייח:
3.6 מערכת עם הגבלה על זמן השהייה של בקשה, זרימה נוספת ומספר אינסופי של מכשירים
תנו לקצב li, שבו מתרחשת רבייה באוכלוסיה של נפח i, ועוצמת המוות mi, המציינת את הקצב שבו מתרחש המוות באוכלוסייה בנפח i, נקבעים על ידי הכלל הבא:
לגרף עוצמות המעבר עבור תהליך נתון של רבייה ומוות יש את הצורה:
איור 6 - גרף של עוצמות מעבר למקרה השישי של תהליך רבייה ומוות
הבה נכתוב את משוואות שיווי המשקל עבור הסתברויות נייחות של מצבים:
כדי למצוא את הציפייה המתמטית, אנו משתמשים בנוסחה. אנו מוצאים שהמספר הממוצע של יישומים במערכת במצב נייח שווה ל:
בוא נאמוד מלמעלה:
לכן:
אנו משיגים את האומדן הבא עבור המספר הממוצע של יישומים במערכת במצב נייח:
סיכום
אז, בחנו את המהות והמודל המתמטי של תהליך הרבייה והמוות, ועל בסיסו, מודלים של ארבעה סוגים בסיסיים של מערכות תור: עם הפסדים והמתנה. נקבע שתהליך מרקוב של רבייה ומוות עם זמן מתמשך הוא תהליך אקראי שיכול לקחת ערכים שלמים לא שליליים; שינויים שבהם יכולים להתרחש בכל נקודת זמן t, בעוד שבכל נקודת זמן הם יכולים לגדול באחד, או לרדת באחת, או להישאר ללא שינוי.
עבודה זו סיפקה גם רקע תיאורטי ודוגמאות לקביעת הציפייה המתמטית לתהליכים שונים של רבייה ומוות, ופתרה בעיות מעשיות.
כך, בעזרת תהליכי הרבייה והמוות, מורכבים מודלים מתמטיים של שליטה בתהליכים שונים, וכן מודלים של תופעות רבות בביולוגיה, בפיסיקה ובתחומים נוספים. כמו כן, תהליכי המוות והרבייה נמצאים בשימוש נרחב בפרקטיקה הנדסית בחקר מערכות טכניות שונות, קשר ישירלתהליכים רבים המתרחשים ב סביבה. תהליכי מרקוב עומדים בבסיס תורת העמידה בתור, אשר בתורה היא הכרחית בכלכלה, בפרט בניהול מיזם ותהליכים שונים המתרחשים בו.
במאמר זה נבחנו תהליכי רבייה ומוות וניתנו נוסחאות לחישוב ההסתברויות המגבילות, ששימשו לתיאור מערכות תורים עם הפסדים והמתנה בהתבסס על זרימת הבקשות הפשוטה ביותר. מתקבלות נוסחאות עבור מאפיינים מסוימים.
רשימת מקורות בשימוש
Wentzel, E.S. תורת התהליכים האקראיים ויישומיה ההנדסיים: ספר לימוד לסטודנטים / E.S. Wentzel, L.A. אובצ'רוב - מהדורה שנייה. - מ.: "בית ספר תיכון", 2000. - 384 עמ'.
מלינקובסקי, יו.וו. הרצאות על תורת העמידה בתור: ספר לימוד לאוניברסיטאות / Yu.V. מלינקובסקי. - גומל: GGU im. F. Skorina, - 184 עמ'. (גרסה אלקטרונית)
ברוכה-ריד, א.ת. אלמנטים של תורת תהליכי מרקוב ויישומיהם / A.T. ברוכה_ריד - מ.: נאוקה, 1969. - 512 עמ'.
סבסטיאנוב, B.A. על כמה סוגים של תהליכי מרקוב / B.A. סבסטיאנוב - כרך 4, גיליון. 4 - Uspekhi Mat Nauk, 1949. - עמ'. 194.
קולמוגורוב, א.נ. מבוא לתורת ההסתברות: ספר לימוד. לאוניברסיטאות / I.G. ז'ורבנקו, A.V. פרוחורוב - מ.: נאוקה, 1982. - 160 עמ'.
שיעורי עזר
זקוק לעזרה בלימוד נושא?
המומחים שלנו ייעצו או יספקו שירותי הדרכה בנושאים שמעניינים אותך.
שלח את הבקשה שלךמציין את הנושא עכשיו כדי לברר על האפשרות לקבל ייעוץ.
בעבודה תיאורטית ומעשית זו, נשקול תכנית של שרשראות מרקוב מתמשכות - מה שנקרא "תכנית מוות ורבייה"
נושא זה רלוונטי ביותר בשל חשיבותם הגבוהה של תהליכי מרקוב בחקר תהליכים כלכליים, סביבתיים וביולוגיים בנוסף, תהליכי מרקוב עומדים בבסיס תורת התור, הנמצאת כיום בשימוש פעיל בתחומים כלכליים שונים, לרבות ניהול תהליכים ארגוניים.
תהליכי מוות ורבייה מרקוב נמצאים בשימוש נרחב בהסבר תהליכים שונים המתרחשים בביוספרה, במערכת האקולוגית וכו'. יש לציין שסוג זה של תהליכי מרקוב קיבל את שמו בדיוק בגלל השימוש הנרחב שלו בביולוגיה, בפרט בהדמיית מוות ורבייה של פרטים מאוכלוסיות שונות.
בעבודה זו ישמשו תהליכי המוות והרבייה לפתרון בעיה, שמטרתה למצוא את המספר המשוער של דבורים באוכלוסייה מסוימת.
חלק תיאורטי
כחלק מהחלק התיאורטי ייכתבו משוואות אלגבריות להסתברויות המגבילות של מצבים. ברור שאם לשתי שרשראות מרקוב יש גרפי מצב זהים ונבדלים רק בערכי העוצמה,
אז אתה יכול מיד למצוא את ההסתברויות המגבילות של מצבים עבור כל אחד מהגרפים בנפרד, זה מספיק כדי לחבר ולפתור בצורה מילולית משוואות עבור אחד מהם, ולאחר מכן להחליף את הערכים המתאימים. עבור צורות גרפים נפוצות רבות, ניתן לפתור בקלות משוואות לינאריות בצורה מילולית.
מאמר זה יתאר תכנית של שרשראות מרקוב מתמשכות - מה שמכונה "תכנית מוות ורבייה".
שרשרת מרקוב רציפה נקראת "תהליך של מוות ורבייה" אם לגרף המצב שלה יש את הצורה המוצגת באיור. 1.1, כלומר ניתן למשוך את כל המצבים לשרשרת אחת, שבה כל אחד ממצבי האמצע (S 2, ..., S n-1) מחובר על ידי ישיר ומשוב עם כל אחד מהמצבים השכנים, והמצבים הקיצוניים ( S 1 , S n) - עם מדינה שכנה אחת בלבד.
כדי לכתוב משוואות אלגבריות עבור ההסתברויות המגבילות של מצבים, ניקח בעיה מסוימת.
דוגמא.המכשיר הטכני מורכב משלוש יחידות זהות; כל אחד מהם יכול להיכשל (להיכשל); הצומת הכושל מתחיל מיד להתאושש. אנו מספרים מצבי מערכת לפי מספר הצמתים הפגומים:
S 0 - כל שלושת הצמתים פועלים;
S 1 - צומת אחד נכשל (משוחזר), שניים פועלים;
S 2 - שני צמתים משוחזרים, אחד מבצעי;
S 3 - כל שלושת הצמתים משוחזרים.
גרף המצב מוצג באיור. 1.2. הגרף מראה שהתהליך המתרחש במערכת הוא תהליך של "מוות ורבייה".
![]()
דפוס המוות והרבייה נמצא לעיתים קרובות במגוון רחב של בעיות מעשיות; לכן, הגיוני לשקול תכנית זו מראש השקפה כלליתולפתור את המערכת המקבילה של משוואות אלגבריות כך שבעתיד, כאשר נתקלים בתהליכים ספציפיים המתרחשים על פי סכמה כזו, לא תצטרכו לפתור את הבעיה בכל פעם מחדש, אלא להשתמש בפתרון מוכן.
אז, בואו נשקול תהליך אקראי של מוות ורבייה עם גרף המצב המוצג באיור. 1.3

בוא נכתוב משוואות אלגבריות להסתברויות של מצבים. עבור המצב הראשון S 1 יש לנו:
עבור המצב השני S 2, סכומי האיברים התואמים לחצים הנכנסים והיוצאים שווים ל:
אבל, מכוח (1.2), נוכל לבטל מונחים שווים זה לזה מימין ומשמאל ונקבל:
במילה אחת, עבור ערכת המוות והרבייה, המונחים התואמים לחצים הניצבים זה מעל זה שווים זה לזה:
איפה קלוקח את כל הערכים מ-2 עד נ.
אז, ההסתברויות המגבילות של מדינות r ъ p 2 > ..., r p inכל תכנית של מוות ורבייה עומדת במשוואות:
 (1.4)
(1.4)
ומצב נורמליזציה:
![]() (1.5)
(1.5)
הבה נפתור מערכת זו באופן הבא: מהמשוואה הראשונה (1.4) אנו מבטאים עמ' 2:
מהשני, תוך התחשבות (1.6), אנו מקבלים
 (1.7)
(1.7)
מהשלישי, תוך התחשבות (1.7):

 (1.8)
(1.8)
נוסחה זו תקפה לכל קמ-2 עד פ.
בואו נשים לב למבנה שלו. המונה מכיל את המכפלה של כל צפיפות הסתברות המעבר (עוצמות) העומדות ליד החצים המכוונים משמאל לימין, מההתחלה ועד לזה שעובר למצב ס ק; במכנה נמצא התוצר של כל העוצמות , עומדים ליד החצים העוברים מימין לשמאל, שוב, מההתחלה ועד לחץ היוצא מהמדינה ס ק. בְּ k=nהמונה יכיל את מכפלת העוצמות , עומדים על כל החצים ההולכים משמאל לימין, ובמכנה - בכל החצים ההולכים מימין לשמאל.
אז כל ההסתברויות באות לידי ביטוי באמצעות אחת מהן: . הבה נחליף את הביטויים האלה בתנאי הנורמליזציה: ![]() . אנחנו מקבלים:
. אנחנו מקבלים:
ההסתברויות הנותרות באות לידי ביטוי באמצעות
 (1.10)
(1.10)
לפיכך, הבעיה של "מוות ורבייה" נפתרה בצורה כללית: נמצאו ההסתברויות המגבילות של מדינות.
חלק מעשי
תהליכי מרקוב, בפרט מוות ורבייה, משמשים לתיאור הפעולה והניתוח של מחלקה רחבה של מערכות עם מספר סופי של מצבים שבהם מתרחשים מעברים חוזרים ממצב אחד לאחר בהשפעת סיבות כלשהן. במערכות כאלה הם מתרחשים באופן אקראי, בפתאומיות ברגע שרירותי בזמן, כאשר אירועים מסוימים (זרימות אירועים) מתרחשים. ככלל, הם משני סוגים: אחד מהם נקרא בדרך כלל לידת חפץ, והשני הוא מותו.
הרבייה הטבעית של מושבות דבורים - נחילות - מנקודת מבט של התהליכים המתרחשים במערכת ברגע הנוכחי בזמן, יכולה להיחשב כתהליך הסתברותי כאשר מושבה בנקודת זמן מסוימת יכולה לעבור ממצב עבודה למצב. אחד רוחש. תלוי ב גורמים שונים, הן טכנולוגיות מבוקרות והן ביולוגיות ואקלימיות מבוקרות בצורה חלשה, היא יכולה להסתיים בנחילות או בהחזרה של המושבה למצב עבודה. במקרה זה, המשפחה יכולה לעבור שוב ושוב למצב כזה או אחר. לפיכך, כדי לתאר את המודל המתמטי של תהליך הנחיל, מותר להשתמש בתיאוריה של תהליכי מרקוב הומוגניים.
עוצמת המעבר של מושבת דבורים למצב נחיל - רבייה - נקבעת במידה רבה על ידי קצב הצטברות של דבורים צעירות לא פעילות. עוצמת המעבר ההפוך - "מוות" - היא החזרה של המושבה למצב עבודה, אשר, בתורו, תלוי בנחיל עצמו, בבחירת הדבורים והדבורים (היווצרות שכבות), בכמות הצוף שנאסף , וכו.
ההסתברות למעבר של מושבת דבורים למצב נחיל תקבע בעיקר על פי עוצמת התהליכים המתרחשים בה המובילים ל- λ , וטכניקות נגד נחילות μ, התלויות בטכנולוגיות המשמשות להפחתת נחילת המושבות. כתוצאה מכך, על מנת להשפיע על התהליכים הנידונים, יש צורך לשנות את העוצמה והכיוון של הזרימות λ ו-μ (איור 1).

מודלים של בחירת חלק מהדבורים מהמשפחה (הגדלת "מוותן") הראה כי ההסתברות להתרחשות של מצב עבודה עולה לוגריתמית, וההסתברות לנחילות פוחתת לוגריתמית. בשיטה נגד נחילות - בחירת 5-7 אלף דבורים ממשפחה (שתיים או שלוש מסגרות סטנדרטיות) - ההסתברות לנחילות תהיה 0.05, וההסתברות למצב עבודה תהיה 0.8; בחירה של יותר משלוש מסגרות של דבורים מפחיתה את הסבירות לנחילות בכמות קטנה מאוד.
בואו נפתור בעיה מעשית הנוגעת לתהליך הנחילות בדבורים.
ראשית, נבנה גרף דומה לגרף באיור 1, עם עוצמות המעבר למצב כזה או אחר.
| |
|
