বিশুদ্ধ প্রজনন প্রক্রিয়া ব্যবহার। বিশুদ্ধ প্রজনন প্রক্রিয়া। প্রজনন এবং মৃত্যুর প্রক্রিয়া
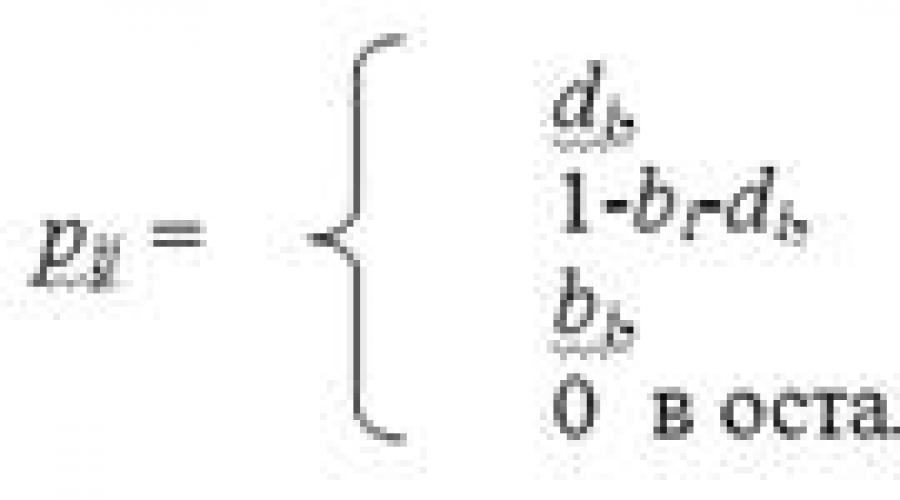
ভূমিকা
এই কাগজে, ক্রমাগত মার্কভ চেইনগুলির প্রকল্পটি বিবেচনা করা হবে - তথাকথিত "ডায়াগ্রাম এবং প্রজনন"
প্রজনন এবং মৃত্যুর প্রক্রিয়া একটি বিচ্ছিন্ন বা ক্রমাগত সময় প্রবাহিত রাষ্ট্রগুলির একটি গণনীয় (সীমাবদ্ধ বা অসীম) সঙ্গে একটি র্যান্ডম প্রক্রিয়া। টাইম র্যান্ডম মুহুর্তে কিছু সিস্টেমটি এক রাজ্য থেকে অন্যের কাছে পাস করে এবং কিছু ঘটনা ঘটে যখন রাজ্যের মধ্যে সংক্রমণ ঘটে। একটি নিয়ম হিসাবে, এই ইভেন্টগুলি দুটি ধরণের: তাদের মধ্যে একটি হল শর্তযুক্তভাবে কিছু বস্তুর জন্ম নামে পরিচিত এবং দ্বিতীয়টি এই বস্তুর মৃত্যু।
অর্থনৈতিক, পরিবেশগত এবং জৈবিক প্রক্রিয়ার গবেষণায় মার্কভ প্রসেসগুলির উচ্চ গুরুত্বের কারণে এই বিষয়টি অত্যন্ত প্রাসঙ্গিক, এ ছাড়া, মার্কভ প্রসেসগুলি ভর পরিষেবার তত্ত্বের অন্তরে রয়েছে, যা বর্তমানে বিভিন্ন অর্থনৈতিক ক্ষেত্রে সক্রিয়ভাবে ব্যবহৃত হয়, এন্টারপ্রাইজে প্রসেসের ব্যবস্থাপনা সহ।
মৃত্যু ও প্রজননের মার্কভ প্রসেসগুলি পদার্থবিজ্ঞান, বায়োস্ফিয়ার, ইকোসিস্টেম ইত্যাদিতে বিভিন্ন প্রক্রিয়ার ব্যাখ্যা দেওয়ার ক্ষেত্রে ব্যাপকভাবে ব্যবহৃত হয়। এটা উল্লেখ করা উচিত যে এই ধরনের মার্কভ প্রসেসগুলি তার নাম পেয়েছেন যা জীববিজ্ঞানের ব্যাপক ব্যবহারের কারণে, বিশেষ করে যখন মৃত্যু এবং বিভিন্ন জনসংখ্যার ব্যক্তিদের প্রজনন মডেল করার সময়।
এই কাগজটি টাস্ট করা হবে, যার উদ্দেশ্যটি প্রজনন ও মৃত্যুর কিছু প্রসেসের জন্য গাণিতিক প্রত্যাশা সংজ্ঞায়িত করা। স্টেশন মোডে সিস্টেমের গড় সংখ্যক অ্যাপ্লিকেশনের গড় সংখ্যা এবং প্রজনন এবং মৃত্যুর প্রক্রিয়াগুলির বিভিন্ন ক্ষেত্রে তৈরি করা হয়।
প্রজনন এবং মৃত্যুর প্রক্রিয়া
প্রজনন এবং মৃত্যুর প্রক্রিয়াগুলি মার্কভ র্যান্ডম প্রসেসগুলির একটি বিশেষ ক্ষেত্রে, যা তবুও, কার্যকরী একটি স্টোকাস্টিক প্রকৃতির সাথে বিযুক্ত সিস্টেমের গবেষণায় ব্যাপকভাবে ব্যবহৃত হয়। প্রজনন এবং মৃত্যুর প্রক্রিয়াটি একটি মার্কভ র্যান্ডম প্রক্রিয়া যা রাজ্য ই থেকে রূপান্তরিত হয় আমি কেবলমাত্র ই -1, ই এবং ই এবং ই + 1 এর সংস্থাগুলির মধ্যে কেবলমাত্র অনুমোদিত। প্রজনন ও মৃত্যুর প্রক্রিয়াটি জৈবিক জনসংখ্যার ভলিউমের পরিবর্তনের বর্ণনা বর্ণনা করার জন্য একটি পর্যাপ্ত মডেল। এই মডেলটি অনুসরণ করে বলা হয়েছে যে এই প্রক্রিয়াটি রাষ্ট্রীয় ই আমি, যদি জনসংখ্যার ভলিউম সদস্যের সমান হয়। এই ক্ষেত্রে, রাজ্য ই থেকে রাষ্ট্র ই আমি + 1 থেকে রূপান্তরটি জন্মের সাথে সামঞ্জস্যপূর্ণ, এবং ই থেকে ই ই -1 -1-মৃত্যু পর্যন্ত রূপান্তরিত হয়, এটি অনুমান করা হয় যে জনসংখ্যার ভলিউমটি বেশি পরিবর্তিত হতে পারে না এক; এর মানে হল প্রজনন প্রক্রিয়া এবং মৃত্যুর জন্য একাধিক একযোগে জন্ম এবং / অথবা মৃত্যু অনুমোদিত নয়।
বিচ্ছিন্ন প্রজনন প্রক্রিয়া এবং মৃত্যু ক্রমাগত তুলনায় কম আকর্ষণীয়, তাই ভবিষ্যতে তারা বিস্তারিত বিবেচনা করা হয় না এবং ক্রমাগত প্রসেস উপর ফোকাস করা হয় না। যাইহোক, এটি উল্লেখ করা উচিত যে প্রায় সমান্তরাল গণনা বিচ্ছিন্ন প্রসেসের জন্য পাস করে। রাজ্য ই থেকে প্রজনন ও মৃত্যুর প্রক্রিয়ার রূপান্তর আমি রাষ্ট্রের কাছে ফিরে এসেছি আমি কেবল বিযুক্ত চেইন মার্কভের জন্য অবিলম্বে আগ্রহের প্রতিনিধিত্ব করি; ক্রমাগত ক্ষেত্রে, তীব্রতা যা বর্তমান অবস্থানে ফিরে আসে তা অসীমের সমান, এবং এই অসীম বাদ দেওয়া হয়েছিল এবং নিম্নরূপ সংজ্ঞায়িত করা হয়েছে:
রাজ্যের মধ্যে সংক্রমণের সম্ভাব্যতা নিয়ে প্রজনন ও মৃত্যুর প্রক্রিয়া চলাকালে

এখানে ডি আমি পছন্দ করি যে পরবর্তী ধাপে (জৈবিক জনসংখ্যার পরিপ্রেক্ষিতে) একটি মৃত্যু হবে যা জনসংখ্যার ভলিউমটি এই পদক্ষেপের সমান বলে যে জনসংখ্যার ভলিউমটি হ্রাস করে। একইভাবে, আমি পরবর্তী ধাপে জন্মের সম্ভাবনা হল জনসংখ্যার ভলিউমের বৃদ্ধির দিকে অগ্রসর হব; এটা এমন সম্ভাবনা যে এই ঘটনাগুলির মধ্যে কেউই ঘটবে না এবং পরবর্তী ধাপে জনসংখ্যার পরিমাণ পরিবর্তন হবে না। শুধুমাত্র এই তিনটি সম্ভাবনার অনুমতি দেওয়া হয়। এটা স্পষ্ট যে, যেহেতু মৃত্যু আসতে পারে না, যদি কিছু ধরনের মারা যায়।
যাইহোক, counterweight অন্তর্দৃষ্টিতে অনুমোদিত হয় যে, যা জন্মের সম্ভাবনার সাথে সামঞ্জস্যপূর্ণ, যখন জনসংখ্যার একক সদস্য না থাকে। যদিও এটি একটি স্বতঃস্ফূর্ত জন্ম বা ঐশ্বরিক সৃষ্টি হিসাবে গণ্য করা যেতে পারে, তবে বিযুক্ত সিস্টেমের তত্ত্ব যেমন একটি মডেল একটি সম্পূর্ণ অর্থপূর্ণ ধারণা। অর্থাৎ, মডেলটি যেমন: জনসংখ্যাটি সিস্টেমের দাবির প্রবাহ, মৃত্যু মানে সিস্টেমের প্রয়োজনীয়তা যত্ন, এবং জন্মটি সিস্টেমের নতুন চাহিদার সাথে সামঞ্জস্যপূর্ণ। এটি স্পষ্ট যে এই ধরনের মডেলটি বিনামূল্যে সিস্টেমে একটি নতুন প্রয়োজন (জন্ম) প্রবেশ করা বেশ সম্ভব। প্রজনন ও মৃত্যুর সাধারণ প্রক্রিয়ার জন্য ট্রানজিটগুলির সম্ভাব্যতা ম্যাট্রিক্স নিম্নলিখিত ফর্মটি রয়েছে:

যদি মার্কভ চেইনটি চূড়ান্ত হয় তবে ম্যাট্রিক্সের পরবর্তী লাইনটি ফর্মটিতে লেখা আছে; এটি হ'ল জনসংখ্যা সর্বাধিক ভলিউম এন পৌঁছে পরে কোন প্রজনন অনুমোদিত হয়। ম্যাট্রিক্স টি শুধুমাত্র প্রধান ত্রিভুজ এবং এটির নিকটতম দুটি ত্রিভুজগুলিতে শূন্য সদস্য রয়েছে। যেমন একটি বিশেষ ধরনের ম্যাট্রিক্স টি এর কারণে, প্রজনন ও মৃত্যুর প্রক্রিয়ার বিশ্লেষণের বিশ্লেষণ অসুবিধাগুলির কারণ হতে পারে না বলে মনে করা স্বাভাবিক। এরপর, আমরা প্রজনন ও মৃত্যুর মাত্র ক্রমাগত প্রক্রিয়াগুলি বিবেচনা করব, যেখানে রাজ্য ই থেকে ট্রানজিটগুলি কেবল প্রতিবেশী রাজ্য ই -1 (মৃত্যু) এবং ই + 1 (জন্ম) তে সম্ভব। আমি প্রজনন তীব্রতা দ্বারা denote; এটি গতির বর্ণনা দেয় যার সাথে আমি জনসংখ্যা ভলিউমের প্রজনন ঘটে। একইভাবে, আমি মাধ্যমে, আমরা মৃত্যুর তীব্রতা চিহ্নিত করে, যা মৃত্যুর ভলিউমের ভলিউমের মধ্যে মৃত্যু ঘটে। মনে রাখবেন যে প্রবর্তিত প্রজনন তীব্রতা এবং মৃত্যু সময় নির্ভর করে না, এবং রাষ্ট্রীয় ই উপর নির্ভর করে, তাই, আমরা মার্কভ টাইপ প্রজনন এবং মৃত্যুর একটি ক্রমাগত একক শৃঙ্খলা অর্জন করি। এই বিশেষ পরিসংখ্যানগুলি চালু করা হয়েছে কারণ তারা সরাসরি বিযুক্ত সিস্টেমের তত্ত্বকে গৃহীত নোটের দিকে পরিচালিত করে। পূর্বে প্রবেশ করা পদে নির্ভর করে আমাদের রয়েছে:
আমি \u003d প্রশ্ন আমি, আমি, আমি + 1 এবং আমি \u003d q I, 1।
শুধুমাত্র নিকটতম সংলগ্ন রাজ্যে অনুমোদিত সংক্রমণের প্রয়োজনীয়তা মানে যেটি এর উপর ভিত্তি করে
আমরা Q II \u003d - (আমি + আমি) প্রাপ্ত। সুতরাং, প্রজনন ও মৃত্যুর সাধারণ একঘেয়ে প্রক্রিয়ার ট্রানজিটগুলির তীব্রতাগুলির ম্যাট্রিক্স ফর্মটি নেয়:

উল্লেখ্য যে প্রধান ত্রিভুজ এবং তার প্রতিবেশী এবং উপরে থেকে ব্যতিক্রমের সাথে ম্যাট্রিক্সের সমস্ত উপাদান শূন্য। ট্রানজিট তীব্রতার সংশ্লিষ্ট গ্রাফ সংশ্লিষ্ট চিত্র (2.1) এ উপস্থাপিত হয়:
চিত্র 2.1 - প্রজনন এবং মৃত্যুর প্রক্রিয়ার জন্য ট্রানজিট তীব্রতা গণনা
প্রজনন ও মৃত্যুর ক্রমাগত প্রক্রিয়াটির আরও সঠিক দৃঢ়সংকল্প নিম্নরূপ: কিছু প্রক্রিয়া প্রজনন ও মৃত্যুর একটি প্রক্রিয়া, যদি এটি অনেক রাজ্যের সাথে মার্কভের একক শৃঙ্খলা (ই 0, ই 1, ই 2, ... ), যদি জন্ম ও মৃত্যু স্বাধীন ঘটনা (এটি সরাসরি মার্কভ সম্পত্তি থেকে অনুসরণ করে) এবং যদি নিম্নলিখিত শর্তগুলি সন্তুষ্ট হয় তবে:
(সময় অন্তর (টি, টি + ডিটি) ঠিক 1 জন্ম, জনসংখ্যা ভলিউম আমি সমান);
(সময় অন্তর ঠিক 1 মৃত্যু (টি, টি + ডিটি) | জনসংখ্যা ভলিউম আমি সমান);
\u003d (সময় অন্তর (টি, টি + ডিটি) এর ঠিক 0 জন্ম হয়। জনসংখ্যার ভলিউম আমি সমান);
\u003d (সময় অন্তর (টি, টি + ডিটি) এর মধ্যে ঠিক 0 মৃত্যু | জনসংখ্যার ভলিউম আমি সমান)।
এভাবে, এন ব্যক্তির জনসংখ্যার জনসংখ্যার একটি নতুন ব্যক্তির জন্মের সম্ভাবনা রয়েছে, এ - সময়কালে এই জনসংখ্যার ব্যক্তিদের মৃত্যুর সম্ভাবনা।
ট্রানজিটের সম্ভাব্যতা কোলমোগোরভের বিপরীত সমীকরণ সন্তুষ্ট করে। সুতরাং সম্ভাব্যতা যে টাইম টি তে প্রজনন ও মৃত্যুর ধারাবাহিক প্রক্রিয়াটি রাষ্ট্রীয় ই (আমি সমান জনসংখ্যার ভলিউম) আকারে নির্ধারণ করা হয়েছে (2.1):

Nonstationary ক্ষেত্রে ডিফারেনশিয়াল সমীকরণের ডিফারেনশিয়াল সমীকরণগুলির সমাধান করার জন্য, যখন সম্ভাব্যতা পিআই (টি), আমি \u003d 0,1,2, ..., এই সময়ের উপর নির্ভর করে, প্রাথমিক সম্ভাব্যতাগুলি PI এর বিতরণ নির্দিষ্ট করার জন্য এটি প্রয়োজনীয় (0), আমি \u003d 0,1,2, ..., টি \u003d 0 এ। উপরন্তু, স্বাভাবিকীকরণ অবস্থা সন্তুষ্ট করা উচিত।
আমরা এখন বিশুদ্ধ প্রজনন সহজতম প্রক্রিয়া বিবেচনা করি, যা একটি প্রক্রিয়া হিসাবে সংজ্ঞায়িত করা হয় যার জন্য আমি \u003d 0 এর জন্য। উপরন্তু, সমস্যাটির আরও সরলীকরণের জন্য, অনুমান করুন যে আমি \u003d সব \u003d 0,1,2, .... সমীকরণে এই মানগুলি প্রতিস্থাপন (2.1) আমরা (2.2):

সরলতার জন্য, আমরা অনুমান করি যে প্রক্রিয়াটি শূন্য সদস্যদের একটি শূন্য মুহূর্তে শুরু হয়, অর্থাৎ:
এখানে থেকে পি 0 (টি) এর জন্য আমরা একটি সমাধান পাই:
সমীকরণের এই সমাধানটি প্রতিস্থাপন (2.2) আমি \u003d 1 এ, আমরা সমীকরণে পৌঁছাতে পারি:
এই ডিফারেনশিয়াল সমীকরণের সমাধানটি অবশ্যই ফর্মটি রয়েছে:
এটি Poisson একটি পরিচিত বিতরণ। সুতরাং, ধ্রুবক তীব্রতা সঙ্গে বিশুদ্ধ প্রজনন প্রক্রিয়া poisson প্রবাহ গঠন জন্ম একটি ক্রম বাড়ে।
বাস্তব পদে সর্বশ্রেষ্ঠ আগ্রহগুলি প্রজনন প্রক্রিয়া এবং স্ট্যাডি মোডে মৃত্যুর সম্ভাব্যতাগুলি প্রতিনিধিত্ব করে। প্রক্রিয়াটি একটি ergodic সম্পত্তি আছে অনুমান, যে, সীমাবদ্ধ আছে
আমরা সীমা সম্ভাবনার সংজ্ঞা পি। আমি। স্থায়ী শাসনব্যবস্থার সম্ভাব্যতা নির্ধারণের জন্য সমীকরণগুলি সরাসরি (2.1) থেকে প্রাপ্ত করা যেতে পারে, যা ডিপি আই (টি) / ডিটি \u003d 0 দিয়ে দেওয়া হয়েছে:
সমীকরণের ফলে সিস্টেমটি স্বাভাবিকীকরণ শর্তের সাথে সমাধান করা হয়েছে (2.4):
প্রজনন ও মৃত্যুর প্রক্রিয়াটির প্রতিষ্ঠিত মোডের জন্য সমীকরণ (2.3) এর সিস্টেমটি সরাসরি চিত্র 2.1 তে ট্রানজিটগুলির তীব্রতার গ্রাফ দ্বারা সরাসরি তৈরি করা যেতে পারে, সম্ভাব্যতা প্রবাহগুলির সমতা নীতি প্রয়োগের একটি পৃথক অবস্থানে। উদাহরণস্বরূপ, যদি আপনি ই স্ট্যাডি মোডে ই রাষ্ট্রকে বিবেচনা করেন তবে:
সম্ভাব্যতা প্রবাহের তীব্রতা এবং
সম্ভাবনা থেকে প্রবাহ তীব্রতা।
ভারসাম্যপূর্ণ অবস্থায়, এই দুটি প্রবাহ সমান হতে হবে, এবং তাই আমরা সরাসরি পেতে পারি:
কিন্তু এটি সিস্টেমের প্রথম সমতা (2.3)। একইভাবে, আপনি সিস্টেমের দ্বিতীয় সমতা পেতে পারেন। প্রবাহ সংরক্ষণের উপর একই যুক্তি, যা পূর্বে দেখানো হয়েছিল, কোন বন্ধ সীমানা মাধ্যমে সম্ভাব্য প্রবাহে প্রয়োগ করা যেতে পারে। উদাহরণস্বরূপ, প্রতিটি রাষ্ট্রকে হাইলাইট করার এবং এটির জন্য একটি সমীকরণ তৈরি করার পরিবর্তে, আপনি কনট্যুরগুলির ক্রমটি নির্বাচন করতে পারেন, যার মধ্যে প্রথমটি রাষ্ট্র ই 0, দ্বিতীয়টি হল রাষ্ট্র ই 0 এবং ই 1, এবং তাই, তাই হয় নতুন সীমানা প্রতিটি সময় পরবর্তী রাষ্ট্র। তারপর I-TH কনট্যুরের জন্য (চারপাশের রাজ্য ই 0, ই 1, ..., ই আই -1), সম্ভাব্যতা প্রবাহ সংরক্ষণ নিম্নলিখিত সহজ আকারে লেখা যেতে পারে:
সমতা (2.5) একটি নিয়ম হিসাবে প্রণয়ন করা যেতে পারে: ইনপেশেন্ট মোডে প্রজনন এবং মৃত্যুর সর্বাধিক ব্যবস্থার জন্য, কোনও দুটি সংলগ্ন রাজ্যের মধ্যে সম্ভাব্যতা প্রবাহ সমান।
সমীকরণের ফলে সিস্টেমটি হ্রাসের সমান। সমীকরণের শেষ ব্যবস্থাকে কম্পাইল করার জন্য প্রতিবেশী রাজ্যগুলিকে আলাদা করা একটি উল্লম্ব লাইনটি বহন করা এবং যার ফলে সীমানার মাধ্যমে প্রবাহগুলি সমান করা প্রয়োজন।
সিস্টেমের সমাধান (2.5) গাণিতিক আনয়ন দ্বারা পাওয়া যাবে।
আমি \u003d 1 আমরা আছে
সমীকরণের ধরনটি দেখায় যে সমীকরণের সিস্টেমের সামগ্রিক সমাধান (2.5) এর ফর্মটি রয়েছে:
অথবা, প্রদত্ত, সংজ্ঞা অনুসারে, একটি খালি সেটের কাজটি হল:
সুতরাং, সমস্ত সম্ভাব্যতা পি আমি স্ট্যাডি মোডের জন্য একমাত্র অজানা ধ্রুবক পি 0 এর মাধ্যমে প্রকাশ করা হয়। সমতা (2.4) পি 0 নির্ধারণ করার জন্য একটি অতিরিক্ত শর্ত দেয়। তারপর, আমি সব উপর summing, পি 0 জন্য আমরা (2.7):

আসুন আমরা স্থির সম্ভাবনার অস্তিত্বের ইস্যুতে ফিরে আসি। সম্ভাব্যতা নির্দিষ্ট করা এক্সপ্রেশনগুলির জন্য, প্রয়োজনীয়তা সাধারণত superimposed হয় যাতে পি 0\u003e 0। এটি স্পষ্টতই সংশ্লিষ্ট সমীকরণগুলিতে প্রজনন coefficients এবং মৃত্যুর উপর একটি সীমাবদ্ধতা imposes। মূলত এটি প্রয়োজন যে সিস্টেম কখনও কখনও খালি হয়; আপনি বাস্তব জীবনের উদাহরণে পরিণত হলে এই স্থিতিশীল অবস্থা খুব যুক্তিসঙ্গত মনে হয়। এটি তুলনায় খুব দ্রুত বৃদ্ধি পায়, এটি শেষ বিন্দুতে একটি ইতিবাচক সম্ভাব্যতা সহ, প্রক্রিয়াটি "একটি অসীম দূরবর্তী বিন্দুতে ফেজ স্পেস (0.1, ...) ছেড়ে চলে যাবে?" (জনসংখ্যার ব্যক্তি খুব বেশী হবে)। অন্য কথায়, প্রক্রিয়াটি নিয়মিত হবে না, এবং তারপর সমতা (2.4) ভাঙ্গা হবে। আমরা নিম্নলিখিত দুটি পরিমাণ সংজ্ঞায়িত:

প্রজনন এবং মৃত্যুর প্রক্রিয়া নিয়মিততার জন্য, এটি প্রয়োজনীয় এবং এর 2 \u003d যথেষ্ট।
তার স্থির বন্টনের অস্তিত্বের জন্য, এটি প্রয়োজনীয় এবং 1 এর জন্য যথেষ্ট< .
ই-এর সব রাজ্যের জন্য আমি প্রশ্ন চলার প্রক্রিয়া এবং মৃত্যুর ইগোডিক ছিলাম, এবং সিরিজ এস 1 এর পর্যাপ্ত কনভারজেন্স ছিলাম< , при этом ряд должен расходиться S 2 = . Только эргодический случай приводит к установившимся вероятностям P i , i = 0, 1, 2, …, и именно этот случай представляет интерес. Заметим, что условия эргодичности выполняются, например, когда, начиная с некоторого i, все члены последовательности {} ограничены единицей, т. е. тогда, когда существует некоторое i 0 (и некоторое С<1) такое, что для всех ii 0 выполняется неравенство:
এই বৈষম্যটি একটি সহজ ব্যাখ্যা দেওয়া যেতে পারে: কিছু রাজ্য ই থেকে শুরু হওয়া এবং পরবর্তী পরবর্তী রাজ্যের জন্য, প্রজননের প্রবাহের তীব্রতা মৃত্যুর প্রবাহের তীব্রতার চেয়ে কম হওয়া উচিত।
কখনও কখনও অনুশীলন মধ্যে "বিশুদ্ধ" প্রজনন প্রক্রিয়া আছে। "বিশুদ্ধ" প্রজনন প্রক্রিয়াটি মৃত্যু এবং প্রজনন এমন একটি প্রক্রিয়া, যার মধ্যে সমস্ত মৃত্যু প্রবাহের তীব্রতা শূন্য। রাষ্ট্রগুলির সংখ্যা সীমিত না করেই এই ধরনের প্রক্রিয়াটির গ্রাফ চিত্রগুলিতে দেখানো হয়েছে (2.2):

চিত্র 2.2 - "বিশুদ্ধ" প্রজনন প্রক্রিয়ার জন্য ট্রানজিট তীব্রতার গ্রাফ
একইভাবে, "পরিষ্কার" মৃত্যুর ধারণাটি চালু করা হয়। "পরিষ্কার" মৃত্যুর প্রক্রিয়াটিকে মৃত্যু এবং প্রজননের এই ধরনের প্রক্রিয়া বলা হয়, যার মধ্যে সমস্ত প্রজনন প্রবাহের তীব্রতা শূন্য। রাজ্যের সংখ্যা সীমিত না করে এই ধরনের প্রক্রিয়াটির গ্রাফ চিত্রটিতে দেখানো হয়েছে:

চিত্র 2.3 - "বিশুদ্ধ" মৃত্যুর প্রক্রিয়ার জন্য ট্রানজিট তীব্রতা গণনা
এই ধরনের প্রক্রিয়ার জন্য কোলমোগোরভ সমীকরণ সিস্টেম সমীকরণের সিস্টেম থেকে প্রাপ্ত করা যেতে পারে (2.1), যার মধ্যে প্রবাহ প্রক্রিয়ার সমস্ত তীব্রতা শূন্যের সমান প্রবাহিত করা প্রয়োজন :.
POISSON প্রক্রিয়ার সর্বাধিক সাধারণীকরণটি ধারণার অধীনে প্রাপ্ত হয় যে জাম্পের সম্ভাব্যতাগুলি সিস্টেমের বর্তমান অবস্থাতে নির্ভর করতে পারে। এই নিম্নলিখিত প্রয়োজনীয়তা আমাদের বাড়ে।
Postulates। (i) রাষ্ট্র থেকে সরাসরি রূপান্তরটি কেবল রাষ্ট্রের পক্ষে সম্ভব। (ii) যদি সিস্টেমটি একটি রাষ্ট্রের মধ্যে থাকে তবে (শর্তাধীন) পরবর্তীতে স্বল্প সময়ের ব্যবধানে একটি লাফের সম্ভাবনা বেশি তারপর হিসাবে (শর্তাধীন) এই ব্যবধানে একাধিক লাফের সম্ভাবনা।
এই ধারণার একটি স্বাতন্ত্র্যসূচক বৈশিষ্ট্য হল যে সিস্টেমটি কোন বিশেষ অবস্থায় ব্যয় করে এমন সময় কোন ভূমিকা পালন করে না; হঠাৎ রাষ্ট্র পরিবর্তন সম্ভব, তবে সিস্টেমটি এক অবস্থায় থাকে, তবে এটি বয়স হয় না।
এটি সম্ভবত সময়ের সাথে সাথে সিস্টেমটি একটি রাজ্যে থাকে। এই ফাংশনগুলি ডিফারেনশিয়াল সমীকরণের সিস্টেমটিকে সন্তুষ্ট করে, যা পূর্ববর্তী অনুচ্ছেদের কারণে তৈরি করা যেতে পারে যা পূর্ববর্তী অনুচ্ছেদের (5) দ্বারা প্রতিস্থাপিত হয়
সুতরাং, আমরা ডিফারেনশিয়াল সমীকরণ প্রধান সিস্টেম প্রাপ্ত
 (2)
(2)
Poisson প্রক্রিয়ার মধ্যে, এটি অনুমান করা স্বাভাবিক ছিল যে সময় 0 সময়, সিস্টেমটি প্রাথমিক রাষ্ট্রের বাইরে আসে। সিস্টেমটি একটি ইচ্ছাকৃত প্রাথমিক রাষ্ট্রের বাইরে আসে যখন আমরা আরো সাধারণ কেসটি স্বীকার করতে পারি। তারপর আমরা যে পেতে
এই প্রাথমিক শর্তাবলী একক সিস্টেমের সমাধান সংজ্ঞায়িত করে (2)। (নির্দিষ্টভাবে, ). অনেক লেখক দ্বারা স্বাধীনভাবে প্রদর্শিত জন্য স্পষ্ট সূত্র, কিন্তু আমাদের জন্য তারা আগ্রহ প্রতিনিধিত্ব করে না।
উদাহরণ। তেজস্ক্রিয় ক্ষয়. কণার নির্গমনের ফলে বা রেডিয়াস, একটি তেজস্ক্রিয় পরমাণু, ইউরেনিয়াম বলে, অন্য প্রজাতির একটি পরমাণুতে পরিণত হতে পারে। প্রতিটি দৃশ্য একটি সম্ভাব্য রাষ্ট্র, এবং যখন প্রক্রিয়াটি আয় করে, তখন আমরা রূপান্তরগুলির একটি ক্রম পেতে পারি। গৃহীত শারীরিক তত্ত্ব অনুযায়ী, পরমাণু একটি রাজ্যে না হওয়া পর্যন্ত ট্রানজিটের সম্ভাব্যতা অপরিবর্তিত থাকে এবং এই অনুমানটি আমাদের প্রাথমিক ধারণার মধ্যে একটি অভিব্যক্তি খুঁজে পায়। অতএব, এই প্রক্রিয়াটি ডিফারেনশিয়াল সমীকরণ (2) (সত্য, সুপরিচিত পদার্থবিজ্ঞানী) দ্বারা বর্ণিত হয়েছে। যদি - চূড়ান্ত অবস্থা, যার থেকে অন্য কোন সংক্রমণ অসম্ভব, তারপর সিস্টেম (2) ভাঙ্গা হয়। (যখন আমরা স্বয়ংক্রিয়ভাবে পেতে পারি)।
বেলারুশ প্রজাতন্ত্রের শিক্ষা মন্ত্রণালয়
শিক্ষা প্রতিষ্ঠা
"গোমেল স্টেট ইউনিভার্সিটি
ফ্রান্সিস স্কোরিনা পরে নামকরণ "
গাণিতিক অনুষদ
অর্থনৈতিক সাইবারনেটিকস এবং সম্ভাব্যতা তত্ত্ব বিভাগ
কোর্স প্রকল্প
প্রজনন এবং মৃত্যু প্রসেসের স্থিতিশীল বৈশিষ্ট্য
নির্বাহক:
Bukhovets ভিক্টোরিয়া
আলেকজান্ডারোভনা
বৈজ্ঞানিক উপদেষ্টা:
অনুষদের প্রধান,
Malinkovsky Yuri।
Vladimirovich.
Gomel 2011।
ভূমিকা
প্রজনন এবং মৃত্যুর প্রক্রিয়া
সাধারণ ভর রক্ষণাবেক্ষণ সিস্টেমের ক্ষেত্রে প্রজনন এবং মৃত্যুর প্রক্রিয়াগুলির উদাহরণ
ভর রক্ষণাবেক্ষণ সিস্টেমের জন্য গাণিতিক প্রত্যাশা 3 এর সংজ্ঞা এম / এম / এন
4 ভর রক্ষণাবেক্ষণ সিস্টেমের জন্য গাণিতিক প্রত্যাশার সংজ্ঞা এম / এম / এন / এন
প্রজনন এবং মৃত্যুর কিছু প্রসেসের জন্য গাণিতিক প্রত্যাশা সংজ্ঞা
রৈখিকভাবে ক্রমবর্ধমান জন্ম তীব্রতা এবং চতুর্ভুজভাবে মৃত্যুর তীব্রতা বৃদ্ধির সাথে প্রজনন এবং মৃত্যুর 2 প্রক্রিয়া
4 অতিরিক্ত প্রবাহ এবং যন্ত্রের অসীম সংখ্যা
আবেদন থাকার সময় জন্য সীমাবদ্ধতা সঙ্গে 5 সিস্টেম
অ্যাপ্লিকেশন থাকার সময়, অতিরিক্ত স্ট্রিম এবং অসীম সংখ্যক যন্ত্রের জন্য সীমাবদ্ধতা 6 সিস্টেম
উপসংহার
ভর রক্ষণাবেক্ষণ গাণিতিক প্রত্যাশা
ভূমিকা
এই কাগজে, ক্রমাগত মার্কভ চেইনগুলির প্রকল্পটি বিবেচনা করা হবে - তথাকথিত "ডায়াগ্রাম এবং প্রজনন"
প্রজনন এবং মৃত্যুর প্রক্রিয়া একটি বিচ্ছিন্ন বা ক্রমাগত সময় প্রবাহিত রাষ্ট্রগুলির একটি গণনীয় (সীমাবদ্ধ বা অসীম) সঙ্গে একটি র্যান্ডম প্রক্রিয়া। টাইম র্যান্ডম মুহুর্তে কিছু সিস্টেমটি এক রাজ্য থেকে অন্যের কাছে পাস করে এবং কিছু ঘটনা ঘটে যখন রাজ্যের মধ্যে সংক্রমণ ঘটে। একটি নিয়ম হিসাবে, এই ইভেন্টগুলি দুটি ধরণের: তাদের মধ্যে একটি হল শর্তযুক্তভাবে কিছু বস্তুর জন্ম নামে পরিচিত এবং দ্বিতীয়টি এই বস্তুর মৃত্যু।
অর্থনৈতিক, পরিবেশগত এবং জৈবিক প্রক্রিয়ার গবেষণায় মার্কভ প্রসেসগুলির উচ্চ গুরুত্বের কারণে এই বিষয়টি অত্যন্ত প্রাসঙ্গিক, এ ছাড়া, মার্কভ প্রসেসগুলি ভর পরিষেবার তত্ত্বের অন্তরে রয়েছে, যা বর্তমানে বিভিন্ন অর্থনৈতিক ক্ষেত্রে সক্রিয়ভাবে ব্যবহৃত হয়, এন্টারপ্রাইজে প্রসেসের ব্যবস্থাপনা সহ।
মৃত্যু ও প্রজননের মার্কভ প্রসেসগুলি পদার্থবিজ্ঞান, বায়োস্ফিয়ার, ইকোসিস্টেম ইত্যাদিতে বিভিন্ন প্রক্রিয়ার ব্যাখ্যা দেওয়ার ক্ষেত্রে ব্যাপকভাবে ব্যবহৃত হয়। এটা উল্লেখ করা উচিত যে এই ধরনের মার্কভ প্রসেসগুলি তার নাম পেয়েছেন যা জীববিজ্ঞানের ব্যাপক ব্যবহারের কারণে, বিশেষ করে যখন মৃত্যু এবং বিভিন্ন জনসংখ্যার ব্যক্তিদের প্রজনন মডেল করার সময়।
এই কাগজটি টাস্ট করা হবে, যার উদ্দেশ্যটি প্রজনন ও মৃত্যুর কিছু প্রসেসের জন্য গাণিতিক প্রত্যাশা সংজ্ঞায়িত করা। স্টেশন মোডে সিস্টেমের গড় সংখ্যক অ্যাপ্লিকেশনের গড় সংখ্যা এবং প্রজনন এবং মৃত্যুর প্রক্রিয়াগুলির বিভিন্ন ক্ষেত্রে তৈরি করা হয়।
1. প্রজনন এবং মৃত্যুর প্রক্রিয়া
প্রজনন এবং মৃত্যুর প্রক্রিয়াগুলি মার্কভ র্যান্ডম প্রসেসগুলির একটি বিশেষ ক্ষেত্রে, যা তবুও, কার্যকরী একটি স্টোকাস্টিক প্রকৃতির সাথে বিযুক্ত সিস্টেমের গবেষণায় ব্যাপকভাবে ব্যবহৃত হয়। প্রজনন এবং মৃত্যুর প্রক্রিয়া একটি মার্কভ র্যান্ডম প্রক্রিয়া যা রাষ্ট্র থেকে রূপান্তর আমি শুধুমাত্র প্রতিবেশী রাজ্যে অনুমোদিত আমি -1। ই। আমি এবং ই। আমি +1। । প্রজনন ও মৃত্যুর প্রক্রিয়াটি জৈবিক জনসংখ্যার ভলিউমের পরিবর্তনের বর্ণনা বর্ণনা করার জন্য একটি পর্যাপ্ত মডেল। এই মডেলটি অনুসরণ করে, তারা বলে যে প্রক্রিয়াটি একটি রাজ্যে আমি যদি জনসংখ্যার ভলিউম সদস্যের সমান হয়। এই ক্ষেত্রে, রাষ্ট্র থেকে রূপান্তর আমি ই। ই। আমি +1। জন্মের সাথে সামঞ্জস্যপূর্ণ, এবং ই থেকে রূপান্তর আমি ই। আমি -1। - মৃত্যু, এটি অনুমান করা হয় যে জনসংখ্যার ভলিউম একাধিকের চেয়ে বেশি নয়; এর মানে হল প্রজনন প্রক্রিয়া এবং মৃত্যুর জন্য একাধিক একযোগে জন্ম এবং / অথবা মৃত্যু অনুমোদিত নয়।
বিচ্ছিন্ন প্রজনন প্রক্রিয়া এবং মৃত্যু ক্রমাগত তুলনায় কম আকর্ষণীয়, তাই ভবিষ্যতে তারা বিস্তারিত বিবেচনা করা হয় না এবং ক্রমাগত প্রসেস উপর ফোকাস করা হয় না। যাইহোক, এটি উল্লেখ করা উচিত যে প্রায় সমান্তরাল গণনা বিচ্ছিন্ন প্রসেসের জন্য পাস করে। রাষ্ট্র থেকে প্রজনন এবং মৃত্যু রূপান্তর প্রক্রিয়া আমি রাষ্ট্র ফিরে ই আমি বিযুক্ত চেইন মার্কভের জন্য শুধুমাত্র সরাসরি আগ্রহের প্রতিনিধিত্ব করে; ক্রমাগত ক্ষেত্রে, তীব্রতা যা বর্তমান অবস্থানে ফিরে আসে তা অসীমের সমান, এবং এই অসীম বাদ দেওয়া হয়েছিল এবং নিম্নরূপ সংজ্ঞায়িত করা হয়েছে:
রাজ্যের মধ্যে সংক্রমণের সম্ভাব্যতা নিয়ে প্রজনন ও মৃত্যুর প্রক্রিয়া চলাকালে
এখানে, ডাইটি এমন সম্ভাবনা যা পরবর্তী ধাপে (জৈবিক জনসংখ্যার পরিপ্রেক্ষিতে) একটি মৃত্যু হবে যা জনসংখ্যার ভলিউমটি এই ধাপের সমান বলে মনে করে। একইভাবে, দ্বিটি পরবর্তী ধাপে জন্মের সম্ভাবনা, জনসংখ্যার ভলিউমের বৃদ্ধি পায়; এটা এমন সম্ভাবনা যে এই ঘটনাগুলির মধ্যে কেউই ঘটবে না এবং পরবর্তী ধাপে জনসংখ্যার পরিমাণ পরিবর্তন হবে না। শুধুমাত্র এই তিনটি সম্ভাবনার অনুমতি দেওয়া হয়। এটা স্পষ্ট যে, যেহেতু মৃত্যু আসতে পারে না, যদি কিছু ধরনের মারা যায়।
যাইহোক, counterweight অন্তর্দৃষ্টিতে অনুমোদিত হয় যে, যা জন্মের সম্ভাবনার সাথে সামঞ্জস্যপূর্ণ, যখন জনসংখ্যার একক সদস্য না থাকে। যদিও এটি একটি স্বতঃস্ফূর্ত জন্ম বা ঐশ্বরিক সৃষ্টি হিসাবে গণ্য করা যেতে পারে, তবে বিযুক্ত সিস্টেমের তত্ত্ব যেমন একটি মডেল একটি সম্পূর্ণ অর্থপূর্ণ ধারণা। অর্থাৎ, মডেলটি যেমন: জনসংখ্যাটি সিস্টেমের দাবির প্রবাহ, মৃত্যু মানে সিস্টেমের প্রয়োজনীয়তা যত্ন, এবং জন্মটি সিস্টেমের নতুন চাহিদার সাথে সামঞ্জস্যপূর্ণ। এটি স্পষ্ট যে এই ধরনের মডেলটি বিনামূল্যে সিস্টেমে একটি নতুন প্রয়োজন (জন্ম) প্রবেশ করা বেশ সম্ভব। প্রজনন ও মৃত্যুর সাধারণ প্রক্রিয়ার জন্য ট্রানজিটগুলির সম্ভাব্যতা ম্যাট্রিক্স নিম্নলিখিত ফর্মটি রয়েছে:
যদি মার্কভ চেইনটি চূড়ান্ত হয় তবে ম্যাট্রিক্সের পরবর্তী লাইনটি ফর্মটিতে লেখা আছে; এটি হ'ল জনসংখ্যা সর্বাধিক ভলিউম এন পৌঁছে পরে কোন প্রজনন অনুমোদিত হয়। ম্যাট্রিক্স টি শুধুমাত্র প্রধান ত্রিভুজ এবং এটির নিকটতম দুটি ত্রিভুজগুলিতে শূন্য সদস্য রয়েছে। যেমন একটি বিশেষ ধরনের ম্যাট্রিক্স টি এর কারণে, প্রজনন ও মৃত্যুর প্রক্রিয়ার বিশ্লেষণের বিশ্লেষণ অসুবিধাগুলির কারণ হতে পারে না বলে মনে করা স্বাভাবিক। এরপর, আমরা প্রজনন ও মৃত্যুর মাত্র ক্রমাগত প্রক্রিয়াগুলি বিবেচনা করব, যার মধ্যে ইআই -1 (মৃত্যু) এবং ইআই + 1 (জন্ম) প্রতিবেশী রাজ্যগুলিতেই ইইয়ের রাষ্ট্রের সংক্রমণ সম্ভব। লি দ্বারা প্রজনন তীব্রতা দ্বারা নির্দেশ করুন; এটি গতির বর্ণনা দেয় যার সাথে আমি জনসংখ্যা ভলিউমের প্রজনন ঘটে। একইভাবে, এমআই এর মাধ্যমে, আমরা মৃত্যুর তীব্রতা চিহ্নিত করে, যা মৃত্যুর ভলিউমের ভলিউমের মধ্যে মৃত্যু ঘটে। মনে রাখবেন যে প্রবর্তিত প্রজনন তীব্রতা ও মৃত্যু কখনোই নির্ভর করে না এবং রাষ্ট্রীয় ইআইআইয়ের উপর নির্ভর করে, তাই আমরা মার্কভ টাইপের প্রজনন ও মৃত্যুর একটি ক্রমাগত একক শৃঙ্খলা অর্জন করি। এই বিশেষ পরিসংখ্যানগুলি চালু করা হয়েছে কারণ তারা সরাসরি বিযুক্ত সিস্টেমের তত্ত্বকে গৃহীত নোটের দিকে পরিচালিত করে। পূর্বে প্রবেশ করা পদে নির্ভর করে আমাদের রয়েছে:
li \u003d qi, আমি + 1 এবং mi \u003d qi, I-1।
শুধুমাত্র নিকটতম সংলগ্ন রাজ্যে অনুমোদিত সংক্রমণের প্রয়োজনীয়তা মানে যেটি এর উপর ভিত্তি করে
আমরা QII \u003d - (এমআই + লি) প্রাপ্ত। সুতরাং, প্রজনন ও মৃত্যুর সাধারণ একঘেয়ে প্রক্রিয়ার ট্রানজিটগুলির তীব্রতাগুলির ম্যাট্রিক্স ফর্মটি নেয়:
উল্লেখ্য যে প্রধান ত্রিভুজ এবং তার প্রতিবেশী এবং উপরে থেকে ব্যতিক্রমের সাথে ম্যাট্রিক্সের সমস্ত উপাদান শূন্য। ট্রানজিট তীব্রতার সংশ্লিষ্ট গ্রাফ সংশ্লিষ্ট চিত্র (2.1) এ উপস্থাপিত হয়:
চিত্র 2.1 - প্রজনন এবং মৃত্যুর প্রক্রিয়ার জন্য ট্রানজিট তীব্রতা গণনা
প্রজনন ও মৃত্যুর ক্রমাগত প্রক্রিয়াটির আরও সঠিক দৃঢ়সংকল্প নিম্নরূপ: কিছু প্রক্রিয়া প্রজনন ও মৃত্যুর একটি প্রক্রিয়া, যদি এটি একাধিক রাজ্যের সাথে একটি একক markov চেইন (E0, E1, E2, ...), যদি জন্ম ও মৃত্যু স্বাধীন ঘটনা (এটি সরাসরি মার্কভ সম্পত্তি থেকে সরাসরি অনুসরণ করে) এবং যদি নিম্নলিখিত শর্তগুলি সন্তুষ্ট হয় তবে:
1) (সময় অন্তর (টি, টি +? টি) ঠিক 1 জন্ম, জনসংখ্যা ভলিউম আমি সমান);
2) (সময় অন্তর (টি, টি +? টি) মধ্যে ঠিক 1 মৃত্যু | জনসংখ্যার ভলিউম আমি সমান);
3) \u003d (সময় অন্তর (টি, টি +? টি) এর ঠিক 0 জন্মের সময় | জনসংখ্যার ভলিউম আমি সমান);
4) \u003d (টাইম বিরতির ঠিক 0 মৃত্যু (টি, টি +? টি) | জনসংখ্যার ভলিউম আমি সমান)।
এভাবে, এন ব্যক্তির জনসংখ্যার জনসংখ্যার একটি নতুন ব্যক্তির জন্মের সম্ভাবনা রয়েছে, এ - সময়কালে এই জনসংখ্যার ব্যক্তিদের মৃত্যুর সম্ভাবনা।
ট্রানজিটের সম্ভাব্যতা কোলমোগোরভের বিপরীত সমীকরণ সন্তুষ্ট করে। সুতরাং, সময়ের সাথে সাথে প্রজনন ও মৃত্যুর ক্রমাগত প্রক্রিয়াটি স্টেট ইআইআই (জনসংখ্যার ভলিউমটি আমি সমান) আকারে নির্ধারণ করা হয়েছে (2.1):
অ্যান্টিশনারি ক্ষেত্রে ডিফারেনশিয়াল সমীকরণের ফলে সিস্টেমটি সমাধান করার জন্য, যখন সম্ভাব্যতা পিআই (টি), আমি \u003d 0,1,2, ..., এই সময়ের উপর নির্ভর করে, প্রাথমিক সম্ভাব্যতা পাই বিতরণ করা প্রয়োজন (0), আমি \u003d 0,1,2, ..., টি \u003d 0 এ। উপরন্তু, স্বাভাবিকীকরণ অবস্থা সন্তুষ্ট করা উচিত।
এখন বিশুদ্ধ প্রজনন সহজতম প্রক্রিয়া বিবেচনা করুন, যা একটি প্রক্রিয়া হিসাবে সংজ্ঞায়িত করা হয় যার জন্য Mi \u003d 0 এর জন্য I. উপরন্তু, সমস্যাটির আরও সরলীকরণের জন্য, অনুমান করুন যে li \u003d l সমস্ত \u003d 0,1,2, .... সমীকরণে এই মানগুলি প্রতিস্থাপন (2.1) আমরা (2.2):
সরলতার জন্য, আমরা অনুমান করি যে প্রক্রিয়াটি শূন্য সদস্যদের একটি শূন্য মুহূর্তে শুরু হয়, অর্থাৎ:
তাই P0 (টি) জন্য আমরা একটি সমাধান পেতে:
সমীকরণের এই সমাধানটি প্রতিস্থাপন (2.2) আমি \u003d 1 এ, আমরা সমীকরণে পৌঁছাতে পারি:
এই ডিফারেনশিয়াল সমীকরণের সমাধানটি অবশ্যই ফর্মটি রয়েছে:
এটি Poisson একটি পরিচিত বিতরণ। সুতরাং, ধ্রুবক তীব্রতা সঙ্গে বিশুদ্ধ প্রজনন প্রক্রিয়া আমি poisson প্রবাহ গঠন জন্ম একটি ক্রম বাড়ে।
বাস্তব পদে সর্বশ্রেষ্ঠ আগ্রহগুলি প্রজনন প্রক্রিয়া এবং স্ট্যাডি মোডে মৃত্যুর সম্ভাব্যতাগুলি প্রতিনিধিত্ব করে। প্রক্রিয়াটি একটি ergodic সম্পত্তি আছে অনুমান, যে, সীমাবদ্ধ আছে
আসুন পাই পাইয়ের সীমা সম্ভাবনার সংজ্ঞাটি চালু করি। স্টেশন মোডের সম্ভাব্যতা নির্ধারণের জন্য সমীকরণগুলি সরাসরি (2.1) থেকে প্রাপ্ত করা যেতে পারে, যা ডিপিআই (টি) / ডিটি \u003d 0 এর সাথে দেওয়া হয়েছে:
সমীকরণের ফলে সিস্টেমটি স্বাভাবিকীকরণ শর্তের সাথে সমাধান করা হয়েছে (2.4):
প্রজনন ও মৃত্যুর প্রক্রিয়াটির প্রতিষ্ঠিত মোডের জন্য সমীকরণ (2.3) এর সিস্টেমটি সরাসরি চিত্র 2.1 তে ট্রানজিটগুলির তীব্রতার গ্রাফ দ্বারা সরাসরি তৈরি করা যেতে পারে, সম্ভাব্যতা প্রবাহগুলির সমতা নীতি প্রয়োগের একটি পৃথক অবস্থানে। উদাহরণস্বরূপ, যদি আপনি স্থির মোডে ইআই স্ট্যাটাসটি বিবেচনা করেন তবে:
সম্ভাব্যতা প্রবাহের তীব্রতা এবং
সম্ভাবনা থেকে প্রবাহ তীব্রতা।
ভারসাম্যপূর্ণ অবস্থায়, এই দুটি প্রবাহ সমান হতে হবে, এবং তাই আমরা সরাসরি পেতে পারি:
কিন্তু এটি সিস্টেমের প্রথম সমতা (2.3)। একইভাবে, আপনি সিস্টেমের দ্বিতীয় সমতা পেতে পারেন। প্রবাহ সংরক্ষণের উপর একই যুক্তি, যা পূর্বে দেখানো হয়েছিল, কোন বন্ধ সীমানা মাধ্যমে সম্ভাব্য প্রবাহে প্রয়োগ করা যেতে পারে। উদাহরণস্বরূপ, প্রতিটি রাষ্ট্রকে আলাদা করার পরিবর্তে এবং এটির জন্য একটি সমীকরণ তৈরি করার পরিবর্তে, আপনি কনট্যুরগুলির ক্রমটি নির্বাচন করতে পারেন, যার মধ্যে প্রথমটি রাজ্য E0, দ্বিতীয় রাষ্ট্র E0 এবং E1, এবং তাই পরবর্তী অবস্থাটি সহ প্রতিটি সময় সহ অন্য রাষ্ট্র। তারপর I-TH কনট্যুরের জন্য (আশপাশের রাজ্য E0, E1, ..., EI-1), সম্ভাব্যতা প্রবাহ নিম্নলিখিত সহজ আকারে লেখা যেতে পারে:
সমতা (2.5) একটি নিয়ম হিসাবে প্রণয়ন করা যেতে পারে: ইনপেশেন্ট মোডে প্রজনন এবং মৃত্যুর সর্বাধিক ব্যবস্থার জন্য, কোনও দুটি সংলগ্ন রাজ্যের মধ্যে সম্ভাব্যতা প্রবাহ সমান।
সমীকরণের ফলে সিস্টেমটি হ্রাসের সমান। সমীকরণের শেষ ব্যবস্থাকে কম্পাইল করার জন্য প্রতিবেশী রাজ্যগুলিকে আলাদা করা একটি উল্লম্ব লাইনটি বহন করা এবং যার ফলে সীমানার মাধ্যমে প্রবাহগুলি সমান করা প্রয়োজন।
সিস্টেমের সমাধান (2.5) গাণিতিক আনয়ন দ্বারা পাওয়া যাবে।
আমি \u003d 1 আমরা আছে
সমীকরণের ধরনটি দেখায় যে সমীকরণের সিস্টেমের সামগ্রিক সমাধান (2.5) এর ফর্মটি রয়েছে:
অথবা, প্রদত্ত, সংজ্ঞা অনুসারে, একটি খালি সেটের কাজটি হল:
সুতরাং, স্ট্যাডি মোডের জন্য PI এর সমস্ত সম্ভাব্যতা শুধুমাত্র অজানা ধ্রুবক P0 এর মাধ্যমে প্রকাশ করা হয়। সমতা (2.4) একটি অতিরিক্ত শর্ত দেয় যা আপনাকে P0 নির্ধারণ করতে দেয়। তারপর, আমি সব উপর summing দ্বারা, P0 এর জন্য আমরা (2.7):
আসুন পাই পাইয়ের স্থায়ী সম্ভাবনার অস্তিত্বের বিষয়টি চালু করি। সম্ভাব্যতা সংজ্ঞায়িত করার জন্য প্রাপ্ত অভিব্যক্তিগুলির জন্য, প্রয়োজনীয়তাটি সাধারণত p0\u003e 0 পর্যন্ত সুপারিমড করা হয়। এটি স্পষ্টতই সংশ্লিষ্ট সমীকরণগুলিতে প্রজনন coefficients এবং মৃত্যুর উপর একটি সীমাবদ্ধতা imposes। মূলত এটি প্রয়োজন যে সিস্টেম কখনও কখনও খালি হয়; আপনি বাস্তব জীবনের উদাহরণে পরিণত হলে এই স্থিতিশীল অবস্থা খুব যুক্তিসঙ্গত মনে হয়। এটি তুলনায় খুব দ্রুত বৃদ্ধি পায়, এটি শেষ বিন্দুতে একটি ইতিবাচক সম্ভাব্যতা সহ, প্রক্রিয়াটি "একটি অসীম দূরবর্তী বিন্দুতে ফেজ স্পেস (0.1, ...) ছেড়ে চলে যাবে?" (জনসংখ্যার ব্যক্তি খুব বেশী হবে)। অন্য কথায়, প্রক্রিয়াটি নিয়মিত হবে না, এবং তারপর সমতা (2.4) ভাঙ্গা হবে। আমরা নিম্নলিখিত দুটি পরিমাণ সংজ্ঞায়িত:
প্রজনন এবং মৃত্যুর প্রক্রিয়া নিয়মিততার জন্য, এটি প্রয়োজনীয় এবং S2 \u003d যথেষ্ট।
তার স্থির বন্টন অস্তিত্বের জন্য, এটি প্রয়োজনীয় এবং S1 যথেষ্ট< .
প্রজনন ও মৃত্যুর প্রক্রিয়ার ইআইআইয়ের সকল রাজ্যের জন্য, এটি প্রয়োজনীয় এবং সিরিজ S1 এর কনভারজেন্সের জন্য যথেষ্ট এবং যথেষ্ট< , при этом ряд должен расходиться S2 = . Только эргодический случай приводит к установившимся вероятностям Pi, i = 0, 1, 2, …, и именно этот случай представляет интерес. Заметим, что условия эргодичности выполняются, например, когда, начиная с некоторого i, все члены последовательности {} ограничены единицей, т. е. тогда, когда существует некоторое i0 (и некоторое С<1) такое, что для всех ii0 выполняется неравенство:
এই বৈষম্যটি একটি সহজ ব্যাখ্যা দেওয়া যেতে পারে: কিছু রাজ্য ইআই থেকে শুরু করে এবং পরবর্তী পরবর্তী রাজ্যের জন্য, প্রজনন প্রবাহের তীব্রতা মৃত্যুর প্রবাহের তীব্রতার চেয়ে কম হওয়া উচিত।
কখনও কখনও অনুশীলন মধ্যে "বিশুদ্ধ" প্রজনন প্রক্রিয়া আছে। "বিশুদ্ধ" প্রজনন প্রক্রিয়াটি মৃত্যু এবং প্রজনন এমন একটি প্রক্রিয়া, যার মধ্যে সমস্ত মৃত্যু প্রবাহের তীব্রতা শূন্য। রাষ্ট্রগুলির সংখ্যা সীমিত না করেই এই ধরনের প্রক্রিয়াটির গ্রাফ চিত্রগুলিতে দেখানো হয়েছে (2.2):
চিত্র 2.2 - "বিশুদ্ধ" প্রজনন প্রক্রিয়ার জন্য ট্রানজিট তীব্রতার গ্রাফ
একইভাবে, "পরিষ্কার" মৃত্যুর ধারণাটি চালু করা হয়। "পরিষ্কার" মৃত্যুর প্রক্রিয়াটিকে মৃত্যু এবং প্রজননের এই ধরনের প্রক্রিয়া বলা হয়, যার মধ্যে সমস্ত প্রজনন প্রবাহের তীব্রতা শূন্য। রাজ্যের সংখ্যা সীমিত না করে এই ধরনের প্রক্রিয়াটির গ্রাফ চিত্রটিতে দেখানো হয়েছে:
চিত্র 2.3 - "বিশুদ্ধ" মৃত্যুর প্রক্রিয়ার জন্য ট্রানজিট তীব্রতা গণনা
এই ধরনের প্রক্রিয়ার জন্য কোলমোগোরভ সমীকরণ সিস্টেম সমীকরণের সিস্টেম থেকে প্রাপ্ত করা যেতে পারে (2.1), যার মধ্যে প্রবাহ প্রক্রিয়ার সমস্ত তীব্রতা শূন্যের সমান প্রবাহিত করা প্রয়োজন :.
2. সাধারণ ভর রক্ষণাবেক্ষণ সিস্টেমের ক্ষেত্রে মৃত্যু ক্ষতির উদাহরণ
ভর রক্ষণাবেক্ষণ সিস্টেমের জন্য গাণিতিক প্রত্যাশার 1 সংজ্ঞা এম / এম / 1
বিবেচনায় ভর রক্ষণাবেক্ষণ সিস্টেমটি নিম্নলিখিত ট্রানজিট গ্রাফের সাথে প্রজনন এবং মৃত্যুর প্রক্রিয়া (চিত্র 3.1):
চিত্র 3.1 - এম / এম / 1 সিস্টেমের জন্য রূপান্তর তীব্রতা গণনা করুন
মৃত্যু ও প্রজনন প্রক্রিয়ার জন্য ergodicity এর অবস্থা থেকে, এটি অনুসরণ করে যে ergodic সঙ্গে coincides একটি একক স্টেশন বিতরণ যদি নেটওয়ার্ক লোড অনুপাত বলা হয়। ভারসাম্য সমীকরণটি এমন ফর্ম যেখানে আমরা খুঁজে পাই যে:
সম্ভাব্যতা স্বাভাবিকীকরণ শর্ত (2.4) ব্যবহার করে পাওয়া যেতে পারে, যেখানে এটি থেকে এবং তাই অনুসরণ করে
i.E. স্টেশল মোডে যেমন একটি ভর রক্ষণাবেক্ষণ সিস্টেমের অ্যাপ্লিকেশনগুলির সংখ্যা একটি জ্যামিতিক বিতরণ রয়েছে।
এই বন্টনের উত্পাদনশীল ফাংশন খুঁজে পাওয়া সহজ:
এখান থেকে আমরা স্থির মোডে সিস্টেমে অ্যাপ্লিকেশনগুলির গড় সংখ্যাগুলির জন্য একটি অভিব্যক্তি পাই:
স্পষ্টতই, ভর পরিষেবা সিস্টেমের সারিতে সীমাহীন ক্রমবর্ধমান হয়।
ভর রক্ষণাবেক্ষণ সিস্টেমের জন্য গাণিতিক প্রত্যাশা 2 এর সংজ্ঞা এম / এম / এন / 0
এই অপেক্ষা ছাড়া একটি ক্ষতি সিস্টেম। যদি পরিষেবাটি সমস্ত এন লাইনের দ্বারা দখল করে থাকে এমন সময়ে সিস্টেমটি প্রবেশ করে তবে এটি হারিয়ে যায়। গত শতাব্দীর শুরুতে ড্যানিশ এরলং ইঞ্জিনিয়ারের এই ধরনের একটি সিস্টেম চালু করা হয়েছিল এবং টেলিফোন এক্সচেঞ্জে প্রবেশ করার একটি কল প্রসেসিং মডেল হিসাবে প্রয়োগ করা হয়েছিল। যেমন একটি ভর রক্ষণাবেক্ষণ সিস্টেমের জন্য ট্রানজিট গ্রাফ ফর্ম আছে (চিত্র 3.2):
চিত্র 3.2 - এম / এম / এন / 0 সিস্টেমের জন্য তীব্রতা তীব্রতা গণনা করুন
যেহেতু সিস্টেমের সিস্টেমের সংখ্যা, এবং মার্কভ চেইনটি irreducible হয়, শুধুমাত্র স্থিতিশীল বিতরণ যা ergodic এর সাথে মিলিত হয়, সর্বদা কোনও প্যারামিটারগুলির সাথে থাকে।
এখানে থেকে আমরা পেতে:
সম্ভাব্যতা, সর্বদা হিসাবে, স্বাভাবিককরণ শর্তাবলী (2.4), অবস্থান থেকে পাওয়া যাবে:
সুতরাং, আমরা পেতে:
সিস্টেমে অ্যাপ্লিকেশনগুলির গড় সংখ্যা সম্পর্কের দ্বারা নির্ধারিত হয়:
বড় এন সঙ্গে, আপনি Asymptotics ব্যবহার করতে পারেন।
2.3 ভর রক্ষণাবেক্ষণ সিস্টেম এম / এম / এন জন্য গাণিতিক প্রত্যাশা সংজ্ঞা
এই প্রত্যাশা সঙ্গে একটি মাল্টি-তারের সিস্টেম। সমস্ত এন লাইন অ্যাপ্লিকেশন সার্ভিসিং দ্বারা দখল করা হয়, তাহলে পরিষেবা তীব্রতা সমান। এই সিস্টেমের জন্য ট্রানজিট গ্রাফ একটি দৃশ্য আছে (চিত্র 3.3):
চিত্র 3.3 - এম / এম / এন সিস্টেমের জন্য ট্রানজিটগুলির তীব্রতা গণনা করুন
স্থিতিশীল বন্টন যদি বিদ্যমান থাকে
নিম্নরূপ সমীকরণ সমীকরণ হয়:
যেখানে, পূর্ববর্তী ক্ষেত্রে অনুরূপ, পেতে
এই ক্ষেত্রে স্বাভাবিকীকরণের শর্তগুলি ফর্মটি নেবে:
যেখানে এটি অনুসরণ করে
ইনপ্যাটেন্ট মোডে অ্যাপ্লিকেশনগুলির গড় সংখ্যা সমান
2.4 ভর রক্ষণাবেক্ষণ সিস্টেমের জন্য গাণিতিক প্রত্যাশার সংজ্ঞা এম / এম / এন / এন
এটি একটি সীমিত সংখ্যক স্থানগুলির সাথে একটি বহু-পার্শ্বযুক্ত সিস্টেম। এটি পূর্ববর্তী ভর রক্ষণাবেক্ষণ সিস্টেম থেকে ভিন্ন যে এটি শুধুমাত্র এন জায়গা আছে। অতএব, এই ক্ষেত্রে ট্রান্সশিশনের গ্রাফ ফর্মটি রয়েছে (চিত্র 3.4):
চিত্র 3.4 - এম / এম / এন / এন সিস্টেমের জন্য ট্রানজিটগুলির তীব্রতা গণনা করুন
যেহেতু সিস্টেমের সিস্টেমের সংখ্যা, একমাত্র স্থায়ী বিতরণ সর্বদা কোনও প্যারামিটারগুলির সাথে বিদ্যমান। ভারসাম্য সমীকরণ ফর্ম গ্রহণ করে:
যেখানে এটি সেই ইনপুটেন্ট সম্ভাব্যতাগুলি অনুসরণ করে, পূর্ববর্তী ভর পরিষেবা সিস্টেমের মতো একই ফর্ম রয়েছে, যা শুধুমাত্র সেই পার্থক্য রয়েছে যা তাদের জন্য সংজ্ঞায়িত করা হয়। এভাবে
সম্ভাব্যতা স্বাভাবিকীকরণের শর্তগুলি থেকে নির্ধারিত হয় (2.4):
আপনি কোথায় পাবেন:
সিস্টেমে অ্যাপ্লিকেশনগুলির গড় সংখ্যা সম্পর্কের দ্বারা নির্ধারিত হয়:
3. প্রজনন ও মৃত্যুর কিছু প্রসেসের জন্য গাণিতিক প্রত্যাশা সংজ্ঞা
রৈখিকভাবে ক্রমবর্ধমান জন্ম তীব্রতা এবং মৃত্যু সঙ্গে প্রজনন এবং মৃত্যুর 1 প্রক্রিয়া
চিত্র 1 - প্রজনন ও মৃত্যুর প্রক্রিয়ার প্রথম ক্ষেত্রে ট্রানজিট তীব্রতার গ্রাফ
আমরা স্টুডিওর সম্ভাব্য সম্ভাবনার জন্য সমীকরণের ভারসাম্য লিখি:
গাণিতিক প্রত্যাশা নির্ধারণ করতে, আমরা নিম্নলিখিত সূত্রটি ব্যবহার করি:
যেখানে সূত্র দ্বারা নির্ধারিত হয়।
সুতরাং, নির্দিষ্ট মোডে সিস্টেমে অ্যাপ্লিকেশনগুলির গড় সংখ্যা হল:
3.2 রৈখিকভাবে ক্রমবর্ধমান জন্ম তীব্রতা এবং চতুর্ভুজভাবে মৃত্যুর তীব্রতা বৃদ্ধির সাথে প্রজনন এবং মৃত্যুর প্রক্রিয়া
স্পিড লি, যার সাথে ভলিউম আমি জনসংখ্যা, এবং এমআই এর মৃত্যুর তীব্রতা, যা ভলিউম আমি জনসংখ্যার মধ্যে মৃত্যুতে মৃত্যু ঘটে, তা নিম্নোক্ত নিয়ম দ্বারা নির্ধারিত হয়:
প্রজনন ও মৃত্যুর এই প্রক্রিয়ার জন্য ট্রানজিট তীব্রতার গ্রাফটি ফর্মটি রয়েছে:
চিত্র 2 - প্রজনন ও মৃত্যুর প্রক্রিয়া দ্বিতীয় ক্ষেত্রে ট্রানজিট তীব্রতার গ্রাফ
আমরা স্টুডিওর সম্ভাব্য সম্ভাবনার জন্য সমীকরণের ভারসাম্য লিখি:
রৈখিকভাবে ক্রমবর্ধমান জন্ম তীব্রতা এবং চতুর্ভুজভাবে মৃত্যুর তীব্রতা বৃদ্ধির সাথে প্রজনন এবং মৃত্যুর 3 প্রক্রিয়া
স্পিড লি, যার সাথে ভলিউম আমি জনসংখ্যা, এবং এমআই এর মৃত্যুর তীব্রতা, যা ভলিউম আমি জনসংখ্যার মধ্যে মৃত্যুতে মৃত্যু ঘটে, তা নিম্নোক্ত নিয়ম দ্বারা নির্ধারিত হয়:
প্রজনন এবং মৃত্যুর এই প্রক্রিয়ার জন্য ট্রানজিশন তীব্রতা গ্রাফ ফর্ম আছে
চিত্র 3 - প্রজনন এবং মৃত্যুর প্রক্রিয়া তৃতীয় ক্ষেত্রে ট্রানজিট তীব্রতা গণনা
আমরা স্টুডিওর সম্ভাব্য সম্ভাবনার জন্য সমীকরণের ভারসাম্য লিখি:
একটি গাণিতিক প্রত্যাশা খুঁজে পেতে, আমরা সূত্র ব্যবহার করি। আমরা স্টেশন মোডে অ্যাপ্লিকেশনগুলির গড় সংখ্যাটি হল:
3.4 অতিরিক্ত স্ট্রিম এবং যন্ত্রের অসীম সংখ্যা
স্পিড লি, যার সাথে ভলিউম আমি জনসংখ্যা, এবং এমআই এর মৃত্যুর তীব্রতা, যা ভলিউম আমি জনসংখ্যার মধ্যে মৃত্যুতে মৃত্যু ঘটে, তা নিম্নোক্ত নিয়ম দ্বারা নির্ধারিত হয়:
প্রজনন ও মৃত্যুর এই প্রক্রিয়ার জন্য ট্রানজিট তীব্রতার গ্রাফটি ফর্মটি রয়েছে:
চিত্র 4 - প্রজনন ও মৃত্যুর প্রক্রিয়ার চতুর্থ ক্ষেত্রে ট্রানজিট তীব্রতার গ্রাফ
আমরা স্টুডিওর সম্ভাব্য সম্ভাবনার জন্য সমীকরণের ভারসাম্য লিখি:
একটি গাণিতিক প্রত্যাশা খুঁজে পেতে, আমরা সূত্র ব্যবহার করি। আমরা স্টেশন মোডে অ্যাপ্লিকেশনগুলির গড় সংখ্যাটি হল:
উপরে থেকে একটি অনুমান করা:
এভাবে:
3.5 একটি অ্যাপ্লিকেশন থাকার সময় জন্য সীমাবদ্ধতা সঙ্গে সিস্টেম
স্পিড লি, যার সাথে ভলিউম আমি জনসংখ্যা, এবং এমআই এর মৃত্যুর তীব্রতা, যা ভলিউম আমি জনসংখ্যার মধ্যে মৃত্যুতে মৃত্যু ঘটে, তা নিম্নোক্ত নিয়ম দ্বারা নির্ধারিত হয়:
প্রজনন ও মৃত্যুর এই প্রক্রিয়ার জন্য ট্রানজিট তীব্রতার গ্রাফটি ফর্মটি রয়েছে:
চিত্র 5 - প্রজনন এবং মৃত্যুর প্রক্রিয়া পঞ্চম ক্ষেত্রে জন্য ট্রানজিট তীব্রতা গ্রাফ
আমরা স্টুডিওর সম্ভাব্য সম্ভাবনার জন্য সমীকরণের ভারসাম্য লিখি:
একটি গাণিতিক প্রত্যাশা খুঁজে পেতে, আমরা সূত্র ব্যবহার করি। আমরা স্টেশন মোডে অ্যাপ্লিকেশনগুলির গড় সংখ্যাটি হল:
উপরে থেকে একটি অনুমান করা:
এভাবে:
আমরা স্টেশন মোডে সিস্টেমে অ্যাপ্লিকেশনের গড় সংখ্যাগুলির জন্য নিম্নলিখিত রেটিংটি পেতে পারি:
3.6 সিস্টেমের আবেদন করার সময়, অতিরিক্ত স্ট্রিম এবং অসীম সংখ্যক যন্ত্রের জন্য সীমাবদ্ধতা
স্পিড লি, যার সাথে ভলিউমটি আমি জনসংখ্যা, এবং এমআইয়ের মৃত্যুর তীব্রতা, যা মৃত্যুর ভলিউম আমি জনসংখ্যার মধ্যে মৃত্যুর ঘটে, তা পাঠ্য রুলে নির্ধারিত হয়।
প্রজনন ও মৃত্যুর এই প্রক্রিয়ার জন্য ট্রানজিট তীব্রতার গ্রাফটি ফর্মটি রয়েছে:
চিত্র 6 - প্রজনন এবং মৃত্যুর প্রক্রিয়ার ছয়টি ক্ষেত্রে ট্রানজিট তীব্রতা গণনা
আমরা স্টুডিওর সম্ভাব্য সম্ভাবনার জন্য সমীকরণের ভারসাম্য লিখি:
একটি গাণিতিক প্রত্যাশা খুঁজে পেতে, আমরা সূত্র ব্যবহার করি। আমরা স্টেশন মোডে অ্যাপ্লিকেশনগুলির গড় সংখ্যাটি হল:
উপরে থেকে একটি অনুমান করা:
এভাবে:
আমরা স্টেশন মোডে সিস্টেমে অ্যাপ্লিকেশনের গড় সংখ্যাগুলির জন্য নিম্নলিখিত রেটিংটি পেতে পারি:
উপসংহার
সুতরাং, আমরা প্রজনন ও মৃত্যুর প্রক্রিয়া এবং এর ভিত্তিতে প্রজনন এবং গাণিতিক মডেলটি দেখেছি - চারটি মৌলিক ধরণের ভর পরিষেবা সিস্টেমের মডেলগুলি: ক্ষতি এবং প্রত্যাশাগুলির সাথে। নির্ধারিত যে ক্রমবর্ধমান সময় দিয়ে প্রজনন ও মৃত্যুর মার্কভ প্রক্রিয়াটি এমন একটি র্যান্ডম প্রক্রিয়া বলা হয় যা অনেক অ-নেতিবাচক মানগুলি গ্রহণ করতে পারে; যে কোনও সময়ে এমন পরিবর্তনগুলি ঘটতে পারে, যখন কোনও সময়ে এটি একের পর একের দ্বারা বৃদ্ধি করতে পারে অথবা অপরিবর্তিত থাকতে পারে।
এছাড়াও এই কাগজে, বিভিন্ন প্রজনন ও মৃত্যুর প্রক্রিয়াগুলির জন্য গাণিতিক প্রত্যাশা নির্ধারণের তাত্ত্বিক সার্টিফিকেট এবং উদাহরণগুলি উপস্থাপন করা হয়েছে, বাস্তব কাজগুলি সমাধান করা হয়েছে।
সুতরাং, প্রজনন ও মৃত্যুর প্রক্রিয়াগুলি, বিভিন্ন প্রসেসের নিয়ন্ত্রণের গাণিতিক মডেল, পাশাপাশি জীববিজ্ঞান, পদার্থবিজ্ঞান এবং অন্যান্য এলাকায় অনেকগুলি ঘটনাগুলির মডেলের সাহায্যে। এছাড়াও, বিভিন্ন প্রযুক্তিগত ব্যবস্থার গবেষণায় প্রকৌশল অনুশীলনে মৃত্যু এবং প্রজনন প্রক্রিয়া ব্যাপকভাবে ব্যবহৃত হয়, পরিবেশে ঘটছে এমন অনেক প্রক্রিয়ার সরাসরি সম্পর্ক রয়েছে। Markov প্রক্রিয়াগুলি ভর পরিষেবার তত্ত্বকে আন্ডারল্লি করে, যা অর্থনীতিতে অপরিহার্য, বিশেষ করে এন্টারপ্রাইজ এবং বিভিন্ন প্রক্রিয়াগুলি পরিচালনা করার সময়।
এই কাগজে, প্রজনন এবং মৃত্যুর প্রক্রিয়াগুলি সীমিত সম্ভাব্যতাগুলি গণনা করার জন্য বিবেচিত এবং সূত্রগুলি ব্যবহার করা হয়, যা অ্যাপ্লিকেশনের সহজ প্রবাহের উপর ভিত্তি করে ক্ষতির এবং প্রত্যাশাগুলির সাথে ভর রক্ষণাবেক্ষণ সিস্টেমগুলি বর্ণনা করতে ব্যবহৃত হয়। সূত্র কিছু বৈশিষ্ট্য জন্য প্রাপ্ত করা হয়।
ব্যবহৃত উত্স তালিকা
Ventcel, ইএস র্যান্ডম প্রসেস এবং এর প্রকৌশল অ্যাপ্লিকেশন তত্ত্ব: শিক্ষার্থী টিউটোরিয়াল / ইএসএস Ventcel, এল। Ovcharov - 2nd ed। - এম।: "উচ্চ বিদ্যালয়", 2000. - 384 পি।
Malinkovsky, yu.v. গণ সেবা তত্ত্বের বক্তৃতা: বিশ্ববিদ্যালয় / yu.v. এর জন্য টিউটোরিয়াল। Malinkovsky। - গোমেল: তাদের জিএসইউ। এফ। স্কিরিনা, 184 পি। (বৈদ্যুতিন বৈকল্পিক)
বারুচা রিড, এ। মার্কভ প্রসেস এবং তাদের অ্যাপ্লিকেশন / A.T এর তত্ত্বের উপাদানগুলি Barucha_rid - মি।: বিজ্ঞান, 1969. - 512 পি।
Sevastyanov, বি। এ। কিছু ধরনের মার্কভ প্রসেস / বি। এ। Sevastyanov - টি। 4, ভোল। 4 - উম্ন, 1949. - পি। 194।
Kolmogorov, A.N. সম্ভাব্যতা তত্ত্বের ভূমিকা: গবেষণা। বিশ্ববিদ্যালয়গুলির জন্য / I.G. Zhurbenko, a.v. Prokhorov - মি।: বিজ্ঞান, 1982. - 160 গুলি।
Tutoring.
কোন ভাষা থিম অধ্যয়ন করতে সাহায্য প্রয়োজন?
আমাদের বিশেষজ্ঞদের আগ্রহের বিষয়ের পরামর্শ দেওয়া বা টিউটোরিয়াল পরিষেবাদি থাকবে।
একটি অনুরোধ পাঠান পরামর্শটি গ্রহণ করার সম্ভাবনা সম্পর্কে এখন বিষয়টি শিখতে।
এই তাত্ত্বিক কাজে, ক্রমাগত মার্কভ চেইনগুলির প্রকল্পটি বিবেচনা করা হবে - তথাকথিত "বিচ্ছেদ এবং প্রজনন প্রকল্প"
অর্থনৈতিক, পরিবেশগত এবং জৈবিক প্রক্রিয়ার গবেষণায় মার্কভ প্রসেসগুলির উচ্চ গুরুত্বের কারণে এই বিষয়টি অত্যন্ত প্রাসঙ্গিক, এ ছাড়া, মার্কভ প্রসেসগুলি ভর পরিষেবার তত্ত্বের অন্তরে রয়েছে, যা বর্তমানে বিভিন্ন অর্থনৈতিক ক্ষেত্রে সক্রিয়ভাবে ব্যবহৃত হয়, এন্টারপ্রাইজে প্রসেসের ব্যবস্থাপনা সহ।
মৃত্যুর এবং প্রজননের মার্কভ প্রসেসগুলি ব্যাপকভাবে বায়োস্ফিয়ার, ইকোসিস্টেম ইত্যাদিতে বিভিন্ন প্রক্রিয়াগুলি ব্যাখ্যা করার ক্ষেত্রে ব্যাপকভাবে ব্যবহৃত হয়। এটি উল্লেখ করা উচিত যে এই ধরনের মার্কভ প্রসেসগুলি জীববিজ্ঞানের ব্যাপক ব্যবহারের কারণে তার নামটি সঠিকভাবে পেয়েছে, বিশেষ করে মৃত্যু এবং ব্যক্তিগত জনসংখ্যার প্রজননকে সিমুলেশন করে।
এই কাগজে, মৃত্যু ও প্রজনন প্রক্রিয়াগুলি সমস্যা সমাধানে ব্যবহার করা হবে, যার উদ্দেশ্যটি পৃথক জনসংখ্যার মধ্যে একটি আনুমানিক পরিমাণ মৌমাছি খুঁজে বের করতে হবে।
তাত্ত্বিক অংশ
তাত্ত্বিক অংশের অংশ হিসাবে, সীমা সম্ভাবনার জন্য বীজগণিত সমীকরণ লিখিত হবে। স্পষ্টতই, যদি মার্কভের দুটি ধারাবাহিক চেইনগুলি একই রাষ্ট্রের গ্রাফ থাকে এবং কেবল তীব্রতা মূল্যের মধ্যেই আলাদা থাকে,
আপনি আলাদাভাবে প্রতিটি গ্রাফের জন্য রাজ্যের সীমিত সম্ভাব্যতাগুলি অবিলম্বে খুঁজে পেতে পারেন, এটি তাদের মধ্যে একটি সমীকরণের চিঠিতে কম্পাইল এবং সমাধানের জন্য যথেষ্ট, এবং তারপরে সংশ্লিষ্ট মূল্যের পরিবর্তে বিকল্পটি বিকল্প। গ্রাফের অনেক সাধারণ পরিসংখ্যানের জন্য, রৈখিক সমীকরণগুলি সহজেই একটি অক্ষরে সমাধান করা হয়।
এই কাগজে, ক্রমাগত মার্কভ চেইনগুলির প্রকল্পটি বর্ণনা করা হবে - তথাকথিত "মৃত্যু এবং প্রজনন" ডায়াগ্রাম "।
মার্কভ ক্রমাগত চেইনটিকে "মৃত্যুর প্রক্রিয়া এবং প্রজনন প্রক্রিয়া" বলা হয়, যদি তার গ্রাফগুলি চিত্রের উপস্থিতি উপস্থিত থাকে। 1.1, অর্থাৎ সমস্ত রাজ্যে এক শৃঙ্খলে পৌঁছানো যেতে পারে যার মধ্যে প্রতিটি রাজ্যের (এস 2, ..., এস এন -1) প্রতিটি সংলগ্ন রাষ্ট্রগুলির সাথে সরাসরি এবং প্রতিক্রিয়ার সাথে সম্পর্কিত এবং চরম রাষ্ট্রগুলির সাথে সম্পর্কিত এস 1, এস এন) - শুধুমাত্র একটি প্রতিবেশী রাষ্ট্র সঙ্গে।
সীমার সম্ভাব্যতাগুলির জন্য বীজগণিত সমীকরণ রেকর্ড করতে, কিছু ধরণের কাজ নিন।
উদাহরণ। প্রযুক্তিগত ডিভাইস তিনটি অভিন্ন নোড গঠিত; তাদের প্রতিটি ব্যর্থ হতে পারে (প্রত্যাখ্যান); প্রত্যাখ্যান নোড অবিলম্বে পুনরুদ্ধার শুরু হয়। ত্রুটিযুক্ত নোডের সংখ্যা দ্বারা সিস্টেম স্টেটস সংখ্যা:
এস 0 - তিনটি নোড ভাল হয়;
এস 1. - এক নোড প্রত্যাখ্যান (পুনরুদ্ধার), দুই ভাল হয়;
গুলি 2 - দুটি নোড পুনরুদ্ধার করা হয়, এক কাজ করছে;
গুলি 3 - তিনটি নোড পুনরুদ্ধার করা হয়।
গণনা রাজ্যের চিত্র দেখানো হয়। 1.2। গ্রাফ থেকে এটি স্পষ্ট যে সিস্টেমে প্রবাহিত প্রক্রিয়াটি "মৃত্যু এবং প্রজনন" প্রক্রিয়া।
![]()
মৃত্যু ও প্রজনন প্রকল্পটি প্রায়শই প্রচুর পরিমাণে ব্যবহারিক কাজগুলিতে পাওয়া যায়; অতএব, সাধারণভাবে এই প্রকল্পটি বিবেচনা করতে এবং বীজগণিত সমীকরণের সংশ্লিষ্ট সিস্টেমের সমাধান করার জন্য, যাতে ভবিষ্যতে, যেমন একটি পরিকল্পনার ভিত্তিতে নির্দিষ্ট প্রক্রিয়াগুলির সাথে বৈঠক করে, তখন প্রতিটি সময় সমস্যাটি সমাধান করবেন না, কিন্তু ব্যবহার করার জন্য প্রস্তুত তৈরি সমাধান।
সুতরাং, ডুমুর দেখানো রাজ্যগুলির গ্রাফের সাথে মৃত্যু এবং প্রজননের র্যান্ডম প্রক্রিয়া বিবেচনা করুন। 1.3.

আমরা রাষ্ট্রের সম্ভাবনার জন্য বীজগণিত সমীকরণ লিখব। প্রথম রাষ্ট্রের 1 এর জন্য আমাদের আছে:
দ্বিতীয় রাজ্যের ২ এর জন্য, অন্তর্মুখী এবং বহির্গামী তীরগুলির সাথে সংশ্লিষ্ট সদস্যদের পরিমাণ সমান:
কিন্তু, (1.2) এর দ্বারা, আপনি সঠিকভাবে কাটতে পারেন এবং একে অপরের সদস্যদের সমান এবং পেতে পারেন:
একটি শব্দে, মৃত্যু ও প্রজনন প্রকল্পের জন্য, একে অপরের উপরে দাঁড়িয়ে তীরের সাথে সংশ্লিষ্ট সদস্য একে অপরের সমান:
কোথায় কে। 2 থেকে সব মান লাগে এন।
সুতরাং, রাজ্যের সীমা সম্ভাব্যতা আর কে P 2 \u003e. ..., পি মৃত্যু এবং প্রজনন কোন অঙ্কন সমীকরণ সন্তুষ্ট:
 (1.4)
(1.4)
এবং স্বাভাবিকীকরণ অবস্থা:
![]() (1.5)
(1.5)
আমরা নিম্নরূপ এই সিস্টেমটি সমাধান করব: প্রথম সমীকরণ থেকে (1.4) এক্সপ্রেস পি 2:
দ্বিতীয় থেকে, অ্যাকাউন্ট গ্রহণ (1.6), আমরা পেতে
 (1.7)
(1.7)
তৃতীয় থেকে, অ্যাকাউন্টে (1.7):

 (1.8)
(1.8)
এই সূত্র কোন জন্য বৈধ কে। থেকে 2 থেকে পি।
তার গঠন মনোযোগ দিতে। সংখ্যার মধ্যে, বাম থেকে ডানে নির্দেশিত তীরগুলির দ্বারা দাঁড়িয়ে থাকা ট্রান্সিশন (তীব্রতা) এর সম্ভাব্যতাগুলির সম্ভাব্যতাগুলির একটি পণ্য রয়েছে যা শুরুতে এবং পর্যন্ত একটি রাষ্ট্রের মধ্যে যায় এস কে। ; Denominator মধ্যে - সব তীব্রতা কাজ , ডানদিকে যাওয়া তীরের পাশে দাঁড়িয়ে, আবার, শুরু থেকে এবং পর্যন্ত রাজ্য থেকে বেরম্বন পর্যন্ত এস কে। । জন্য কে \u003d এন। ঘনত্ব সংখ্যা সংখ্যার মধ্যে দাঁড়ানো হবে , বাম ডানদিকে যাচ্ছেন সব তীরের সাথে দাঁড়িয়ে থাকা এবং সূচক-তে - সমস্ত তীর ডানদিকে যাচ্ছেন।
সুতরাং, তাদের মধ্যে সমস্ত সম্ভাব্যতা প্রকাশ করা হয় :. স্বাভাবিকীকরণ অবস্থায় এই এক্সপ্রেশনগুলি বিকল্প করুন: ![]() । আমরা পেতে:
। আমরা পেতে:
অবশিষ্ট সম্ভাব্যতা মাধ্যমে প্রকাশ করা হয়
 (1.10)
(1.10)
সুতরাং, "মৃত্যু ও প্রজনন" এর কাজটি সাধারণ আকারে সমাধান করা হয়েছে: রাষ্ট্রগুলির সীমা সম্ভাব্যতা পাওয়া যায়।
ব্যবহারিক অংশ
মার্কভ প্রসেসগুলি বিশেষ করে মৃত্যু এবং প্রজনন, কাজটি বর্ণনা করার জন্য ব্যবহৃত হয় এবং একটি সীমাবদ্ধ শ্রেণির একটি বিস্তৃত শ্রেণির বিশ্লেষণের জন্য ব্যবহৃত হয় যা কোনও কারণে কোনও কারণে প্রভাবশালী সংস্থার পুনরাবৃত্তি ঘটে। যেমন সিস্টেমে, তারা এলোমেলোভাবে ঘটে, কিছু ঘটনা ঘটে যখন একটি নির্বিচারে মুহূর্তের সময় hopped হয় (ইভেন্ট প্রবাহ)। একটি নিয়ম হিসাবে, তারা দুটি ধরনের: তাদের মধ্যে একটি প্রচলিতভাবে বস্তুর জন্ম নামে পরিচিত, এবং দ্বিতীয়টি তার মৃত্যু।
মৌমাছি পরিবারের প্রাকৃতিক প্রজনন - বর্তমান সময়ে সিস্টেমে প্রবাহিত প্রসেসের দৃষ্টিকোণ থেকে, একটি সম্ভাব্য প্রক্রিয়া হিসাবে বিবেচনা করা সম্ভব হয় যখন একটি নির্দিষ্ট সময়ে পরিবারটি কর্মরত রাষ্ট্র থেকে ঘুরে যেতে পারে । বিভিন্ন কারণের উপর নির্ভর করে, নিয়ন্ত্রিত প্রযুক্তিগত এবং দুর্বল নিয়ন্ত্রিত জৈবিক ও জলবায়ু উভয়ই, এটি শেষ বা পরিবারকে একটি কাজের অবস্থায় ফিরিয়ে দিতে পারে। একই সময়ে, পরিবারটি বারবার এক জিনিসে স্যুইচ করতে পারে, তারপর অন্য অবস্থায়। সুতরাং, প্রক্রিয়ার গাণিতিক মডেলটি বর্ণনা করার জন্য, এটি সমষ্টিগত মার্কভ প্রসেসগুলির তত্ত্ব প্রয়োগ করার অনুমতি দেওয়া হয়।
মৌমাছি রাষ্ট্রের মধ্যে মৌমাছি পরিবারের রূপান্তরের তীব্রতা প্রজনন - মূলত তরুণ অভাবহীন মৌমাছির সংশ্লেষণের হার দ্বারা নির্ধারিত। বিপরীত রূপান্তরের তীব্রতা হল "মৃত্যু" - কাজের অবস্থার জন্য পরিবারের ফেরত, যা প্রকৃতপক্ষে প্রকৃত সময়ের উপর নির্ভর করে, ভাঙ্গন নির্বাচন এবং মৌমাছিগুলির গঠন (মেসেঞ্জারের গঠন), অমৃতের পরিমাণের উপর নির্ভর করে সংগৃহীত, ইত্যাদি
রথ স্টেটে পরিবারের মৌমাছির রূপান্তরের সম্ভাব্যতাটি প্রথমে এটির মধ্যে প্রথমে এটির মধ্যে পাস করা প্রক্রিয়াগুলির তীব্রতা দ্বারা নির্ধারিত হবে, যা হ্রাসের জন্য ব্যবহৃত প্রযুক্তির উপর নির্ভর করে, যা হ্রাস করার জন্য ব্যবহৃত প্রযুক্তির উপর নির্ভর করে। পরিবারের রুট। ফলস্বরূপ, আলোচনা করা প্রসেসগুলিকে প্রভাবিত করার জন্য, প্রবাহের তীব্রতা এবং দিক পরিবর্তন করা প্রয়োজন λ এবং μ (চিত্র 1)।

মৌমাছিগুলির একক নির্বাচন মডেলিংয়ের অংশ (তাদের "মৃত্যু") দেখিয়েছে যে, কাজ রাষ্ট্রের ঘটনার সম্ভাবনাটি লগারিথম্যাটিক্যালি, এবং গোলাপের সম্ভাব্যতা লগারিদমগতভাবে হ্রাস পাচ্ছে। বিরোধী-গ্রহণযোগ্য স্থান - 5-7 হাজার মৌমাছি (দুই বা তিনটি স্ট্যান্ডার্ড ফ্রেম) এর একটি পরিবার থেকে নির্বাচন করুন - রোজিয়ামের সম্ভাব্যতা 0.05 হবে, এবং কাজের অবস্থার সম্ভাব্যতা 0.8; মৌমাছি সহ তিনটি ফ্রেমের বেশি নির্বাচন একটি খুব ছোট পরিমাণের সম্ভাবনা হ্রাস করে।
আমরা মৌমাছি এ রডিং প্রক্রিয়ার বিষয়ে বাস্তব টাস্ক সমাধান করব।
একটি শুরুতে, আমরা একটি স্ট্রেনের তীব্রতার সাথে চিত্র 1 এর গ্রাফের মতো একটি গ্রাফ তৈরি করি, একটি রাষ্ট্রের সংক্রমণের তীব্রতা সহ।
| |
|
