सापेक्ष त्रुटि की गणना के लिए सूत्र. पूर्ण और सापेक्ष माप त्रुटियाँ
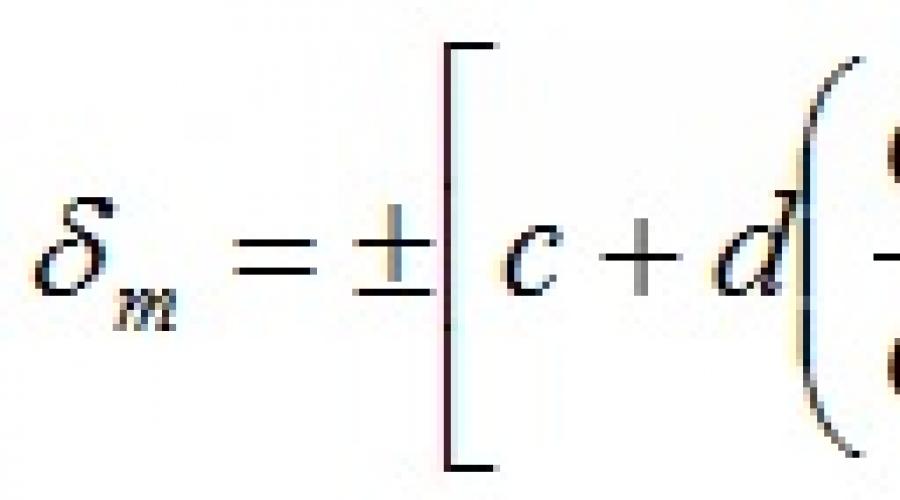
ये भी पढ़ें
किसी भौतिक मात्रा का सही मूल्य बिल्कुल सटीक रूप से निर्धारित करना लगभग असंभव है, क्योंकि कोई भी माप ऑपरेशन कई त्रुटियों या, दूसरे शब्दों में, अशुद्धियों से जुड़ा होता है। त्रुटियों के कारण बहुत भिन्न हो सकते हैं। उनकी घटना अध्ययन के तहत वस्तु की भौतिक विशेषताओं के कारण मापने वाले उपकरण के निर्माण और समायोजन में अशुद्धियों से जुड़ी हो सकती है (उदाहरण के लिए, गैर-समान मोटाई के तार के व्यास को मापते समय, परिणाम यादृच्छिक रूप से निर्भर करता है माप स्थल का चुनाव), यादृच्छिक कारण, आदि।
प्रयोगकर्ता का कार्य परिणाम पर उनके प्रभाव को कम करना है, और यह भी इंगित करना है कि प्राप्त परिणाम सत्य के कितना करीब है।
निरपेक्ष और सापेक्ष त्रुटि की अवधारणाएँ हैं।
अंतर्गत पूर्ण त्रुटिमाप माप परिणाम और मापी गई मात्रा के वास्तविक मूल्य के बीच अंतर को समझेंगे:
∆x i =x i -x और (2)
जहां ∆x i, i-th माप की पूर्ण त्रुटि है, x i _, i-th माप का परिणाम है, x और मापे गए मान का सही मान है।
किसी भी भौतिक माप का परिणाम आमतौर पर इस रूप में लिखा जाता है:
मापे गए मान का अंकगणितीय माध्य मान कहां है, जो वास्तविक मान के सबसे करीब है (x और≈ की वैधता नीचे दिखाई जाएगी), पूर्ण माप त्रुटि है।
समानता (3) को इस प्रकार समझना चाहिए कि मापी गई मात्रा का वास्तविक मान अंतराल [ - , + ] में होता है।
निरपेक्ष त्रुटि एक आयामी मात्रा है; इसका आयाम मापी गई मात्रा के समान है।
पूर्ण त्रुटि लिए गए मापों की सटीकता को पूरी तरह से चित्रित नहीं करती है। वास्तव में, यदि हम समान पूर्ण त्रुटि ± 1 मिमी के साथ 1 मीटर और 5 मिमी लंबे खंडों को मापते हैं, तो माप की सटीकता अतुलनीय होगी। इसलिए, पूर्ण माप त्रुटि के साथ, सापेक्ष त्रुटि की गणना की जाती है।
रिश्तेदारों की गलतीमाप स्वयं मापे गए मान के लिए पूर्ण त्रुटि का अनुपात है:
सापेक्ष त्रुटि एक आयामहीन मात्रा है। इसे प्रतिशत के रूप में व्यक्त किया जाता है:
उपरोक्त उदाहरण में, सापेक्ष त्रुटियाँ 0.1% और 20% हैं। वे एक-दूसरे से स्पष्ट रूप से भिन्न हैं, हालाँकि निरपेक्ष मान समान हैं। सापेक्ष त्रुटि सटीकता के बारे में जानकारी देती है
माप त्रुटियाँ
अभिव्यक्ति की प्रकृति और त्रुटियों के घटित होने के कारणों के अनुसार, उन्हें निम्नलिखित वर्गों में विभाजित किया जा सकता है: वाद्य, व्यवस्थित, यादृच्छिक और चूक (सकल त्रुटियाँ)।
त्रुटियाँ या तो डिवाइस की खराबी के कारण होती हैं, या कार्यप्रणाली या प्रयोगात्मक शर्तों के उल्लंघन के कारण होती हैं, या व्यक्तिपरक प्रकृति की होती हैं। व्यवहार में, उन्हें ऐसे परिणामों के रूप में परिभाषित किया जाता है जो दूसरों से बिल्कुल भिन्न होते हैं। उनकी घटना को खत्म करने के लिए, उपकरणों के साथ काम करते समय सावधानी और सावधानी बरतना आवश्यक है। त्रुटियों वाले परिणामों को विचार से बाहर रखा जाना चाहिए (त्याग दिया जाना चाहिए)।
उपकरण त्रुटियाँ. यदि मापने वाला उपकरण अच्छे कार्य क्रम में है और समायोजित किया गया है, तो उपकरण के प्रकार द्वारा निर्धारित सीमित सटीकता के साथ उस पर माप किया जा सकता है। सूचक उपकरण की उपकरण त्रुटि को उसके पैमाने के सबसे छोटे विभाजन के आधे के बराबर मानने की प्रथा है। डिजिटल रीडआउट वाले उपकरणों में, उपकरण त्रुटि उपकरण पैमाने के एक सबसे छोटे अंक के मूल्य के बराबर होती है।
व्यवस्थित त्रुटियाँ वे त्रुटियाँ हैं जिनका परिमाण और चिह्न एक ही विधि द्वारा और एक ही माप उपकरणों का उपयोग करके किए गए मापों की पूरी श्रृंखला के लिए स्थिर होते हैं।
माप करते समय, न केवल व्यवस्थित त्रुटियों को ध्यान में रखना महत्वपूर्ण है, बल्कि उनका उन्मूलन सुनिश्चित करना भी आवश्यक है।
व्यवस्थित त्रुटियों को पारंपरिक रूप से चार समूहों में विभाजित किया गया है:
1) त्रुटियाँ, जिनकी प्रकृति ज्ञात है और उनका परिमाण काफी सटीक रूप से निर्धारित किया जा सकता है। ऐसी त्रुटि, उदाहरण के लिए, हवा में मापे गए द्रव्यमान में परिवर्तन है, जो तापमान, आर्द्रता, वायु दबाव आदि पर निर्भर करता है;
2) त्रुटियाँ, जिनकी प्रकृति ज्ञात है, लेकिन त्रुटि की भयावहता अज्ञात है। ऐसी त्रुटियों में मापने वाले उपकरण के कारण होने वाली त्रुटियां शामिल हैं: डिवाइस की खराबी, एक पैमाना जो शून्य मान या डिवाइस की सटीकता वर्ग के अनुरूप नहीं है;
3) त्रुटियाँ, जिनके अस्तित्व पर संदेह नहीं किया जा सकता है, लेकिन उनकी भयावहता अक्सर महत्वपूर्ण हो सकती है। ऐसी त्रुटियाँ अक्सर जटिल मापों में होती हैं। ऐसी त्रुटि का एक सरल उदाहरण कुछ नमूनों के घनत्व का माप है जिसमें अंदर एक गुहा है;
4) माप वस्तु की विशेषताओं के कारण होने वाली त्रुटियाँ। उदाहरण के लिए, किसी धातु की विद्युत चालकता को मापते समय, धातु से तार का एक टुकड़ा लिया जाता है। यदि सामग्री में कोई दोष है तो त्रुटियाँ हो सकती हैं - दरार, तार का मोटा होना या असमानता जो इसके प्रतिरोध को बदल देती है।
यादृच्छिक त्रुटियाँ वे त्रुटियाँ हैं जो एक ही मात्रा के बार-बार माप की समान स्थितियों के तहत संकेत और परिमाण में यादृच्छिक रूप से बदलती हैं।
सम्बंधित जानकारी।
कोई भी माप त्रुटियों से मुक्त नहीं है, या, अधिक सटीक रूप से, त्रुटियों के बिना माप की संभावना शून्य के करीब पहुंचती है। त्रुटियों के प्रकार और कारण बहुत विविध हैं और कई कारकों से प्रभावित होते हैं (चित्र 1.2)।
प्रभावित करने वाले कारकों की सामान्य विशेषताओं को विभिन्न दृष्टिकोणों से व्यवस्थित किया जा सकता है, उदाहरण के लिए, सूचीबद्ध कारकों के प्रभाव के अनुसार (चित्र 1.2)।
माप परिणामों के आधार पर, त्रुटियों को तीन प्रकारों में विभाजित किया जा सकता है: व्यवस्थित, यादृच्छिक और त्रुटियाँ।
व्यवस्थित त्रुटियाँ बदले में, वे अपनी घटना और उनकी अभिव्यक्ति की प्रकृति के कारण समूहों में विभाजित हो जाते हैं। उन्हें विभिन्न तरीकों से समाप्त किया जा सकता है, उदाहरण के लिए, संशोधन पेश करके।
चावल। 1.2
यादृच्छिक त्रुटियाँ बदलते कारकों के एक जटिल समूह के कारण होते हैं, जो आमतौर पर अज्ञात होते हैं और उनका विश्लेषण करना मुश्किल होता है। माप परिणाम पर उनके प्रभाव को कम किया जा सकता है, उदाहरण के लिए, संभाव्यता सिद्धांत पद्धति का उपयोग करके प्राप्त परिणामों के आगे सांख्यिकीय प्रसंस्करण के साथ बार-बार माप द्वारा।
को छूट जाए इनमें प्रायोगिक स्थितियों में अचानक परिवर्तन से उत्पन्न होने वाली सकल त्रुटियाँ शामिल हैं। ये त्रुटियाँ भी प्रकृति में यादृच्छिक हैं और एक बार पहचाने जाने पर इन्हें समाप्त किया जाना चाहिए।
माप की सटीकता का आकलन माप त्रुटियों द्वारा किया जाता है, जिन्हें उनकी घटना की प्रकृति के अनुसार वाद्य और पद्धति में और गणना पद्धति के अनुसार पूर्ण, सापेक्ष और कम में विभाजित किया जाता है।
सहायक त्रुटि को मापने वाले उपकरण की सटीकता वर्ग की विशेषता है, जो उसके पासपोर्ट में सामान्यीकृत मुख्य और अतिरिक्त त्रुटियों के रूप में दिया गया है।
व्यवस्थित त्रुटि माप विधियों और उपकरणों की अपूर्णता के कारण है।
निरपेक्ष त्रुटि मापे गए G u और किसी मात्रा के वास्तविक G मानों के बीच का अंतर है, जो सूत्र द्वारा निर्धारित किया जाता है:
Δ=ΔG=G u -G
ध्यान दें कि मात्रा में मापी गई मात्रा का आयाम होता है।
रिश्तेदार त्रुटि समानता से पाई जाती है
δ=±ΔG/G u ·100%
दिया गया त्रुटि की गणना सूत्र (मापने वाले उपकरण की सटीकता वर्ग) का उपयोग करके की जाती है
δ=±ΔG/G मानदंड ·100%
जहां जी मानदंड मापी गई मात्रा का सामान्यीकरण मूल्य है। इसे इसके बराबर लिया जाता है:
क) उपकरण स्केल का अंतिम मान, यदि शून्य चिह्न स्केल के किनारे पर या बाहर है;
बी) यदि शून्य चिह्न पैमाने के अंदर स्थित है, तो संकेतों को ध्यान में रखे बिना पैमाने के अंतिम मूल्यों का योग;
ग) पैमाने की लंबाई, यदि पैमाना असमान है।
किसी उपकरण की सटीकता वर्ग उसके परीक्षण के दौरान स्थापित की जाती है और यह सूत्रों का उपयोग करके गणना की गई एक मानकीकृत त्रुटि है
γ=±ΔG/G मानदंड ·100%, यदिΔजी एम = स्थिरांक

जहां ΔG m डिवाइस की सबसे बड़ी संभावित निरपेक्ष त्रुटि है;
जी के - डिवाइस की माप सीमा का अंतिम मूल्य; सी और डी गुणांक हैं जो डिवाइस के माप तंत्र के डिज़ाइन मापदंडों और गुणों को ध्यान में रखते हैं।
उदाहरण के लिए, निरंतर सापेक्ष त्रुटि वाले वोल्टमीटर के लिए, समानता कायम रहती है
δ एम =±सी
सापेक्ष और घटी हुई त्रुटियाँ निम्नलिखित निर्भरताओं से संबंधित हैं:
ए) कम की गई त्रुटि के किसी भी मूल्य के लिए
δ=±γ·जी मानदंड/जी यू
बी) सबसे बड़ी कम त्रुटि के लिए
δ=±γ m ·G मानदंड/G u
इन संबंधों से यह पता चलता है कि माप करते समय, उदाहरण के लिए वोल्टमीटर के साथ, एक ही वोल्टेज मान पर एक सर्किट में, मापा वोल्टेज जितना कम होगा, सापेक्ष त्रुटि उतनी ही अधिक होगी। और यदि यह वोल्टमीटर गलत तरीके से चुना गया है, तो सापेक्ष त्रुटि मान के अनुरूप हो सकती हैजी एन , जो अस्वीकार्य है. ध्यान दें कि हल की जा रही समस्याओं की शब्दावली के अनुसार, उदाहरण के लिए, वोल्टेज जी = यू को मापते समय, वर्तमान सी = आई को मापते समय, त्रुटियों की गणना के लिए सूत्रों में अक्षर पदनामों को संबंधित प्रतीकों के साथ प्रतिस्थापित किया जाना चाहिए।
उदाहरण 1.1.γ m = 1.0% मान वाला एक वोल्टमीटर, यू एन = जी मानदंड, जी के = 450 वी, वोल्टेज यू यू को 10 वी के बराबर मापें। आइए माप त्रुटियों का अनुमान लगाएं।
समाधान।

उत्तर।माप त्रुटि 45% है. ऐसी त्रुटि के साथ, मापा वोल्टेज को विश्वसनीय नहीं माना जा सकता है।
यदि किसी उपकरण (वोल्टमीटर) को चुनने की संभावनाएं सीमित हैं, तो सूत्र का उपयोग करके गणना की गई संशोधन द्वारा पद्धतिगत त्रुटि को ध्यान में रखा जा सकता है

उदाहरण 1.2. DC सर्किट में वोल्टेज मापते समय V7-26 वोल्टमीटर की पूर्ण त्रुटि की गणना करें। वोल्टमीटर की सटीकता वर्ग अधिकतम कम त्रुटि γ m =±2.5% द्वारा निर्दिष्ट की जाती है। कार्य में प्रयुक्त वोल्टमीटर स्केल सीमा यू मानक = 30 वी है।
समाधान।पूर्ण त्रुटि की गणना ज्ञात सूत्रों का उपयोग करके की जाती है:
![]()
(चूँकि कम हुई त्रुटि, परिभाषा के अनुसार, सूत्र द्वारा व्यक्त की जाती है ![]() , तो यहां से आप पूर्ण त्रुटि पा सकते हैं:
, तो यहां से आप पूर्ण त्रुटि पा सकते हैं: ![]()
उत्तर।ΔU = ±0.75 वी.
माप प्रक्रिया में महत्वपूर्ण चरण परिणामों का प्रसंस्करण और पूर्णांकन नियम हैं। अनुमानित गणना का सिद्धांत, डेटा की सटीकता की डिग्री को जानते हुए, कार्रवाई करने से पहले ही परिणामों की सटीकता की डिग्री का मूल्यांकन करने की अनुमति देता है: सटीकता की उचित डिग्री के साथ डेटा का चयन करने के लिए, परिणाम की आवश्यक सटीकता सुनिश्चित करने के लिए पर्याप्त है, लेकिन कैलकुलेटर को बेकार गणनाओं से बचाने के लिए इतना बढ़िया नहीं; गणना प्रक्रिया को तर्कसंगत बनाएं, इसे उन गणनाओं से मुक्त करें जो सटीक संख्याओं और परिणामों को प्रभावित नहीं करेंगी।
परिणामों को संसाधित करते समय, पूर्णांकन नियम लागू किए जाते हैं।
- नियम 1। यदि छोड़ा गया पहला अंक पांच से अधिक है, तो बचाए गए अंतिम अंक में एक की वृद्धि की जाती है।
- नियम 2. यदि छोड़े गए अंकों में से पहला अंक पांच से कम है, तो कोई वृद्धि नहीं की जाती है।
- नियम 3. यदि छोड़ा गया अंक पांच है और उसके पीछे कोई महत्वपूर्ण अंक नहीं है, तो निकटतम सम संख्या में पूर्णांकन किया जाता है, अर्थात। संग्रहीत अंतिम अंक यदि सम है तो वही रहता है और यदि सम नहीं है तो बढ़ जाता है।
यदि संख्या पांच के पीछे महत्वपूर्ण अंक हैं, तो नियम 2 के अनुसार पूर्णांकन किया जाता है।
किसी एक संख्या को पूर्णांकित करने के लिए नियम 3 को लागू करने से, हम पूर्णांकन की सटीकता में वृद्धि नहीं करते हैं। लेकिन अनेक पूर्णांकों के साथ, अतिरिक्त संख्याएँ लगभग उतनी ही बार घटित होंगी जितनी बार अपर्याप्त संख्याएँ। पारस्परिक त्रुटि मुआवजा परिणाम की सबसे बड़ी सटीकता सुनिश्चित करेगा।
वह संख्या जो स्पष्ट रूप से पूर्ण त्रुटि से अधिक हो (या सबसे खराब स्थिति में उसके बराबर हो) कहलाती है अधिकतम निरपेक्ष त्रुटि.
अधिकतम त्रुटि का परिमाण पूर्णतया निश्चित नहीं है। प्रत्येक अनुमानित संख्या के लिए, इसकी अधिकतम त्रुटि (पूर्ण या सापेक्ष) ज्ञात होनी चाहिए।
जब इसे सीधे तौर पर इंगित नहीं किया जाता है, तो यह समझा जाता है कि अधिकतम निरपेक्ष त्रुटि लिखे गए अंतिम अंक की आधी इकाई है। इसलिए, यदि अधिकतम त्रुटि दर्शाए बिना 4.78 की अनुमानित संख्या दी गई है, तो यह माना जाता है कि अधिकतम निरपेक्ष त्रुटि 0.005 है। इस समझौते के परिणामस्वरूप, आप हमेशा नियम 1-3 के अनुसार पूर्णांकित संख्या की अधिकतम त्रुटि को इंगित किए बिना कर सकते हैं, अर्थात, यदि अनुमानित संख्या अक्षर α द्वारा निरूपित की जाती है, तो
जहां Δn अधिकतम निरपेक्ष त्रुटि है; और δ n अधिकतम सापेक्ष त्रुटि है।
इसके अलावा, परिणामों को संसाधित करते समय, हम उपयोग करते हैं त्रुटि खोजने के नियम योग, अंतर, उत्पाद और भागफल।
- नियम 1। योग की अधिकतम निरपेक्ष त्रुटि व्यक्तिगत पदों की अधिकतम निरपेक्ष त्रुटियों के योग के बराबर होती है, लेकिन शर्तों की त्रुटियों की एक महत्वपूर्ण संख्या के साथ, त्रुटियों का पारस्परिक मुआवजा आमतौर पर होता है, इसलिए योग की सही त्रुटि केवल असाधारण में होती है मामले अधिकतम त्रुटि से मेल खाते हैं या उसके करीब हैं।
- नियम 2. अंतर की अधिकतम निरपेक्ष त्रुटि कम या घटाए जाने वाले अंतर की अधिकतम निरपेक्ष त्रुटियों के योग के बराबर होती है।
अधिकतम निरपेक्ष त्रुटि की गणना करके अधिकतम सापेक्ष त्रुटि आसानी से पाई जा सकती है।
- नियम 3. योग की अधिकतम सापेक्ष त्रुटि (लेकिन अंतर नहीं) पदों की सबसे छोटी और सबसे बड़ी सापेक्ष त्रुटियों के बीच होती है।
यदि सभी पदों में समान अधिकतम सापेक्ष त्रुटि है, तो योग में समान अधिकतम सापेक्ष त्रुटि है। दूसरे शब्दों में, इस मामले में योग की सटीकता (प्रतिशत के संदर्भ में) शब्दों की सटीकता से कम नहीं है।
योग के विपरीत, अनुमानित संख्याओं का अंतर मीनूएंड और सबट्रेंड की तुलना में कम सटीक हो सकता है। परिशुद्धता का नुकसान विशेष रूप से तब अधिक होता है जब मीनूएंड और सबट्रेंड एक दूसरे से बहुत कम भिन्न होते हैं।
- नियम 4. उत्पाद की अधिकतम सापेक्ष त्रुटि लगभग कारकों की अधिकतम सापेक्ष त्रुटियों के योग के बराबर है: δ=δ 1 +δ 2, या, अधिक सटीक रूप से, δ=δ 1 +δ 2 +δ 1 δ 2 जहां δ है उत्पाद की सापेक्ष त्रुटि, δ 1 δ 2 - सापेक्ष त्रुटि कारक।
टिप्पणियाँ:
1. यदि समान संख्या में महत्वपूर्ण अंकों वाली अनुमानित संख्याओं को गुणा किया जाता है, तो उत्पाद में महत्वपूर्ण अंकों की समान संख्या बरकरार रखी जानी चाहिए। संग्रहीत अंतिम अंक पूर्णतः विश्वसनीय नहीं होगा.
2. यदि कुछ कारकों में दूसरों की तुलना में अधिक महत्वपूर्ण अंक हैं, तो गुणा करने से पहले, पहले वाले को पूर्णांकित किया जाना चाहिए, उनमें कम से कम सटीक कारक के रूप में कई अंक या एक और (अतिरिक्त के रूप में) रखना चाहिए, आगे के अंकों को सहेजना बेकार है।
3. यदि यह आवश्यक है कि दो संख्याओं के गुणनफल में एक पूर्व निर्धारित संख्या हो जो पूरी तरह से विश्वसनीय हो, तो प्रत्येक कारक में सटीक अंकों की संख्या (माप या गणना द्वारा प्राप्त) एक और होनी चाहिए। यदि कारकों की संख्या दो से अधिक और दस से कम है, तो प्रत्येक कारक में पूर्ण गारंटी के लिए सटीक अंकों की संख्या आवश्यक सटीक अंकों की संख्या से दो इकाई अधिक होनी चाहिए। व्यवहार में, केवल एक अतिरिक्त अंक लेना ही काफी है।
- नियम 5. भागफल की अधिकतम सापेक्ष त्रुटि लाभांश और भाजक की अधिकतम सापेक्ष त्रुटियों के योग के लगभग बराबर होती है। अधिकतम सापेक्ष त्रुटि का सटीक मान हमेशा अनुमानित से अधिक होता है। अधिकता का प्रतिशत लगभग विभाजक की अधिकतम सापेक्ष त्रुटि के बराबर है।
उदाहरण 1.3. भागफल 2.81: 0.571 की अधिकतम निरपेक्ष त्रुटि ज्ञात कीजिए।
समाधान।लाभांश की अधिकतम सापेक्ष त्रुटि 0.005:2.81=0.2% है; भाजक - 0.005:0.571=0.1%; निजी - 0.2% + 0.1% = 0.3%। भागफल की अधिकतम निरपेक्ष त्रुटि लगभग 2.81 होगी: 0.571·0.0030=0.015
इसका मतलब यह है कि भागफल 2.81:0.571=4.92 में तीसरा महत्वपूर्ण अंक विश्वसनीय नहीं है।
उत्तर। 0,015.
उदाहरण 1.4. सर्किट (चित्र 1.3) के अनुसार जुड़े वोल्टमीटर की रीडिंग की सापेक्ष त्रुटि की गणना करें, जो तब प्राप्त होती है जब हम मानते हैं कि वोल्टमीटर में असीम रूप से बड़ा प्रतिरोध होता है और मापा सर्किट में विकृतियां नहीं लाता है। इस समस्या के लिए माप त्रुटि को वर्गीकृत करें।

चावल। 1.3
समाधान।आइए हम एक वास्तविक वोल्टमीटर की रीडिंग को AND से और एक अनंत उच्च प्रतिरोध वाले वोल्टमीटर की रीडिंग को AND से निरूपित करें। आवश्यक सापेक्ष त्रुटि ![]()
नोटिस जो
तो हम पाते हैं
चूँकि R और >>R और R > r, अंतिम समानता के हर में भिन्न एक से बहुत कम है। इसलिए, आप अनुमानित सूत्र का उपयोग कर सकते हैं ![]() , किसी भी α के लिए λ≤1 के लिए मान्य है। यह मानते हुए कि इस सूत्र में α = -1 और λ= rR (r+R) -1 R और -1, हमें δ ≈ rR/(r+R) R और मिलता है।
, किसी भी α के लिए λ≤1 के लिए मान्य है। यह मानते हुए कि इस सूत्र में α = -1 और λ= rR (r+R) -1 R और -1, हमें δ ≈ rR/(r+R) R और मिलता है।
सर्किट के बाहरी प्रतिरोध की तुलना में वोल्टमीटर का प्रतिरोध जितना अधिक होगा, त्रुटि उतनी ही कम होगी। लेकिन शर्त आर< उत्तर।व्यवस्थित कार्यप्रणाली त्रुटि. उदाहरण 1.5.
डीसी सर्किट (चित्र 1.4) में निम्नलिखित उपकरण शामिल हैं: ए - एमीटर प्रकार एम 330, सटीकता वर्ग के ए = 1.5 माप सीमा आई के = 20 ए के साथ; ए 1 - एमीटर प्रकार एम 366, सटीकता वर्ग के ए1 = 1.0 माप सीमा I के1 = 7.5 ए के साथ। वर्तमान I 2 को मापने में सबसे बड़ी संभावित सापेक्ष त्रुटि और इसके वास्तविक मूल्य की संभावित सीमा का पता लगाएं, यदि उपकरणों ने दिखाया कि I = 8 ,0ए. और मैं 1 = 6.0ए. माप को वर्गीकृत करें. चावल। 1.4 समाधान।हम डिवाइस की रीडिंग से वर्तमान I 2 निर्धारित करते हैं (उनकी त्रुटियों को ध्यान में रखे बिना): I 2 =I-I 1 =8.0-6.0=2.0 A. आइए एमीटर ए और ए 1 के पूर्ण त्रुटि मॉड्यूल खोजें ए के लिए हमारे पास समानता है आइए पूर्ण त्रुटि मॉड्यूल का योग ज्ञात करें: नतीजतन, समान मूल्य का सबसे बड़ा संभावित मूल्य, इस मूल्य के अंशों में व्यक्त, 1 के बराबर है। 10 3 - एक डिवाइस के लिए; 2·10 3 - किसी अन्य डिवाइस के लिए। इनमें से कौन सा उपकरण सबसे सटीक होगा? समाधान।डिवाइस की सटीकता को त्रुटि के व्युत्क्रम द्वारा दर्शाया जाता है (डिवाइस जितना अधिक सटीक होगा, त्रुटि उतनी ही छोटी होगी), अर्थात। पहले डिवाइस के लिए यह 1/(1 . 10 3) = 1000 होगा, दूसरे के लिए - 1/(2 . 10 3) = 500. ध्यान दें कि 1000 > 500. इसलिए, पहला डिवाइस उससे दोगुना सटीक है द्वितीय वाला। त्रुटियों की संगति की जाँच करके इसी तरह के निष्कर्ष पर पहुँचा जा सकता है: 2. 10 3 /1. 10 3 = 2. उत्तर।पहला उपकरण दूसरे से दोगुना सटीक है। उदाहरण 1.6.
डिवाइस के अनुमानित मापों का योग ज्ञात करें। सही वर्णों की संख्या ज्ञात करें: 0.0909 + 0.0833 + 0.0769 + 0.0714 + 0.0667 + 0.0625 + 0.0588+ 0.0556 + 0.0526। समाधान।सभी माप परिणामों को जोड़ने पर, हमें 0.6187 मिलता है। योग की अधिकतम अधिकतम त्रुटि 0.00005·9=0.00045 है. इसका मतलब है कि योग के अंतिम चौथे अंक में 5 इकाइयों तक की त्रुटि संभव है। इसलिए, हम राशि को तीसरे अंक तक पूर्णांकित करते हैं, अर्थात। हज़ारवां, हमें 0.619 मिलता है - एक परिणाम जिसमें सभी चिह्न सही हैं। उत्तर। 0.619. सही अंकों की संख्या दशमलव के तीन अंक है। समस्या इस प्रकार तैयार की गई है: वांछित मात्रा दें जेडअन्य मात्राओं के माध्यम से निर्धारित किया जाता है ए, बी, सी, ... प्रत्यक्ष माप से प्राप्त किया गया जेड = एफ (ए, बी, सी,...) (1.11) फ़ंक्शन का औसत मान और उसके माप की त्रुटि ज्ञात करना आवश्यक है, अर्थात। आत्मविश्वास अंतराल खोजें विश्वसनीयता ए और सापेक्ष त्रुटि के साथ। जहाँ तक, यह (11) के स्थान पर दाईं ओर प्रतिस्थापित करने पर पाया जाता है ए, बी, सी,...उनके औसत मूल्य 3. अप्रत्यक्ष माप के परिणाम के लिए विश्वास अंतराल की आधी-चौड़ाई का अनुमान लगाएं जहां डेरिवेटिव... की गणना की जाती है 4. परिणाम की सापेक्ष त्रुटि निर्धारित करें 5. यदि z की निर्भरता ए, बी, सी,...रूप है और तब निरपेक्ष . 6. अंतिम परिणाम फॉर्म में लिखें z = ± Dz , ε = …% a पर =
… . टिप्पणी: प्रत्यक्ष माप के परिणामों को संसाधित करते समय, आपको निम्नलिखित नियम का पालन करना चाहिए: सभी गणना की गई मात्राओं के संख्यात्मक मानों में मूल (प्रयोगात्मक रूप से निर्धारित) मात्राओं से एक अंक अधिक होना चाहिए। अप्रत्यक्ष माप के लिए, गणना के अनुसार की जाती है अनुमानित गणना के नियम: नियम 1।
अनुमानित संख्याओं को जोड़ते और घटाते समय, आपको यह करना होगा: ए) उस पद का चयन करें जिसमें संदिग्ध अंक का अंक सबसे अधिक है; बी) अन्य सभी पदों को अगले अंक में पूर्णांकित करें (एक अतिरिक्त अंक बरकरार रखा गया है); ग) जोड़ (घटाना) करना; घ) परिणामस्वरूप, अंतिम अंक को पूर्णांकन करके हटा दें (परिणाम के संदिग्ध अंक का अंक पदों के संदिग्ध अंकों के उच्चतम अंकों के साथ मेल खाता है)। उदाहरण: 5.4382·10 5 - 2.918·10 3 + 35.8 + 0.064। इन संख्याओं में, अंतिम महत्वपूर्ण अंक संदिग्ध हैं (गलत अंक पहले ही हटा दिए गए हैं)। आइए इन्हें 543820 – 2918 + 35.8 + 0.064 के रूप में लिखें। यह देखा जा सकता है कि पहले पद में संदिग्ध संख्या 2 का अंक (दहाई) सबसे अधिक है। अन्य सभी संख्याओं को अगले अंक तक पूर्णांकित करने और जोड़ने पर, हमें प्राप्त होता है 543820 - 2918 + 36 + 0 = 540940 = 5.4094 10 5। नियम 2.
अनुमानित संख्याओं को गुणा (विभाजित) करते समय आपको यह करना होगा: a) सबसे कम महत्वपूर्ण अंकों वाली संख्या(संख्याओं) का चयन करें ( महत्वपूर्ण - शून्य के अलावा अन्य संख्याएँ और उनके बीच शून्य); बी) शेष संख्याओं को गोल करें ताकि उनमें चरण ए में आवंटित संख्याओं की तुलना में एक अधिक महत्वपूर्ण अंक हो (एक अतिरिक्त अंक बरकरार रहे); ग) परिणामी संख्याओं को गुणा (विभाजित) करें; घ) परिणामस्वरूप, उतने ही महत्वपूर्ण अंक छोड़ें जितने कम से कम महत्वपूर्ण अंकों वाली संख्याओं में थे। उदाहरण: . नियम 3.
जब एक घात तक बढ़ाया जाता है, तो जड़ निकालते समय, परिणाम में उतने ही महत्वपूर्ण अंक बने रहते हैं जितने मूल संख्या में होते हैं। उदाहरण: नियम 4.
किसी संख्या का लघुगणक ज्ञात करते समय, लघुगणक के मंटिसा में उतने ही महत्वपूर्ण अंक होने चाहिए जितने मूल संख्या में हैं: उदाहरण: अंतिम रिकॉर्डिंग में निरपेक्षत्रुटियाँ ही छोड़ देनी चाहिए एक महत्वपूर्ण आंकड़ा. (यदि यह अंक 1 निकलता है तो इसके बाद दूसरा अंक संग्रहित हो जाता है)। औसत मान को पूर्ण त्रुटि के समान अंक तक पूर्णांकित किया जाता है। उदाहरण के लिए: वी= (375.21 0.03) सेमी 3 = (3.7521 0.0003) सेमी 3। मैं= (5.530 0.013) ए, ए = कार्य - आदेश
सिलेंडर व्यास का निर्धारण.
1. कैलीपर का उपयोग करके, सिलेंडर का व्यास 7 बार (विभिन्न स्थानों और दिशाओं में) मापें। परिणामों को एक तालिका में रिकॉर्ड करें. सम्बंधित जानकारी: मापी गई और सारणीबद्ध मात्राओं में त्रुटियां अप्रत्यक्ष रूप से निर्धारित मूल्य के डीएच औसत की त्रुटियों को निर्धारित करती हैं, और डीएच औसत में सबसे बड़ा योगदान कम से कम सटीक मानों द्वारा किया जाता है, जिनमें अधिकतम सापेक्ष त्रुटि होती है डी. इसलिए, अप्रत्यक्ष माप की सटीकता बढ़ाने के लिए, प्रत्यक्ष माप की समान सटीकता प्राप्त करना आवश्यक है (डी ए, डी बी, डी सी, ...)। अप्रत्यक्ष माप में त्रुटियाँ ढूँढने के नियम: 1. दिए गए फ़ंक्शन का प्राकृतिक लघुगणक ज्ञात करें ln(X = f(A,B,C,…)); 2. दिए गए फ़ंक्शन के पाए गए प्राकृतिक लघुगणक से कुल अंतर (सभी चर पर) ज्ञात करें; 3. अंतर d के चिह्न को पूर्ण त्रुटि D के चिह्न से बदलें; 4. पूर्ण त्रुटियों का सामना करने वाले सभी "माइनस" को बदलें डीए, डीबी, डीसी, ... "पेशेवर" के लिए। परिणाम सबसे बड़ी सापेक्ष त्रुटि का सूत्र है डी एक्सअप्रत्यक्ष रूप से मापा गया मान X: डी एक्स = = जे (ए औसत, बी औसत, सी औसत, ..., डीए औसत, डीबी औसत, डीसी औसत, ...)।(18) पाई गई सापेक्ष त्रुटि के अनुसार डी एक्सअप्रत्यक्ष माप की पूर्ण त्रुटि निर्धारित करें: डीएक्स एवी = डी एक्स। एक्स औसत . (19) अप्रत्यक्ष माप का परिणाम मानक रूप में लिखा जाता है और संख्यात्मक अक्ष पर दर्शाया जाता है: एक्स = (एक्स औसत ± डीХ औसत),इकाई। (20) उदाहरण:
किसी भौतिक राशि की सापेक्ष एवं औसत त्रुटियों का मान ज्ञात कीजिए एल, सूत्र द्वारा अप्रत्यक्ष रूप से निर्धारित: कहाँ π, जी, टी, के, α, β- वे मात्राएँ जिनका मान संदर्भ तालिकाओं से मापा या लिया जाता है और माप परिणामों और सारणीबद्ध डेटा की तालिका में दर्ज किया जाता है (तालिका 1 के समान)। 1. औसत मूल्य की गणना करें एल औसत, तालिका से औसत मानों को (21) में प्रतिस्थापित करने पर – π औसत, जी औसत, टी औसत, के औसत, α औसत, β औसत। 2. सबसे बड़ी सापेक्ष त्रुटि निर्धारित करें δ एल: ए)। लघुगणक सूत्र (21): बी)। परिणामी अभिव्यक्ति (22) विभेदित है: सी) अंतर डी के चिह्न को Δ से बदलें, और पूर्ण त्रुटियों के सामने "माइनस" को "प्लस" से बदलें, और सबसे बड़ी सापेक्ष त्रुटि के लिए एक अभिव्यक्ति प्राप्त करें δ एल: डी)। माप की तालिका से इनपुट मात्राओं और उनकी त्रुटियों के औसत मूल्यों को परिणामी अभिव्यक्ति में प्रतिस्थापित करते हुए, गणना करें δ एल. 3. फिर पूर्ण त्रुटि की गणना करें ΔL औसत: परिणाम को मानक रूप में दर्ज किया जाता है और अक्ष पर ग्राफ़िक रूप से दर्शाया जाता है एल: माप त्रुटि का प्राथमिक अनुमान मापन विशेष तकनीकी साधनों - माप, माप उपकरणों की सहायता से प्रयोगात्मक रूप से भौतिक मात्रा का मूल्य ज्ञात करना है। माप माप का एक साधन है जो किसी दिए गए आकार की भौतिक मात्रा को पुन: उत्पन्न करता है - माप की एक इकाई, इसका गुणज या भिन्नात्मक मान। उदाहरण के लिए, वजन 1 किलो, 5 किलो, 10 किलो। एक मापने वाला उपकरण एक मापने वाला उपकरण है जिसे एक पर्यवेक्षक द्वारा प्रत्यक्ष धारणा के लिए सुलभ रूप में जानकारी को मापने का संकेत उत्पन्न करने के लिए डिज़ाइन किया गया है। एक मापने वाला उपकरण आपको प्रत्यक्ष या अप्रत्यक्ष रूप से मापे गए मूल्य की माप से तुलना करने की अनुमति देता है। मापों को भी प्रत्यक्ष और अप्रत्यक्ष में विभाजित किया गया है। प्रत्यक्ष माप में, मात्रा का वांछित मान सीधे मूल (प्रायोगिक) डेटा से पाया जाता है। अप्रत्यक्ष माप में, किसी मात्रा का वांछित मूल्य इस मात्रा और प्रत्यक्ष माप के अधीन मात्राओं के बीच ज्ञात संबंध के आधार पर पाया जाता है। माप सिद्धांत भौतिक घटनाओं का एक समूह है जिस पर माप आधारित होते हैं। माप पद्धति सिद्धांतों और माप उपकरणों का उपयोग करने के लिए तकनीकों का एक सेट है। किसी भौतिक मात्रा का मूल्य, जो आदर्श रूप से गुणात्मक और मात्रात्मक शब्दों में किसी दिए गए वस्तु की संबंधित संपत्ति को प्रतिबिंबित करेगा, भौतिक मात्रा का सही मूल्य है। किसी भौतिक राशि को मापने से जो मान ज्ञात होता है वह माप का परिणाम होता है। मापे गए मान के वास्तविक मान से माप परिणाम का विचलन माप त्रुटि है। पूर्ण माप त्रुटि माप त्रुटि है, जो मापा मूल्य की इकाइयों में व्यक्त की जाती है और परिणाम और मापा मूल्य के वास्तविक मूल्य के बीच अंतर के बराबर होती है। मापी गई मात्रा के वास्तविक मान से पूर्ण त्रुटि का अनुपात सापेक्ष माप त्रुटि है। माप त्रुटि में योगदान में माप उपकरणों में त्रुटियां (वाद्य या उपकरण त्रुटि), माप पद्धति की अपूर्णता, उपकरण पैमाने पर पढ़ने में त्रुटि, माप के साधनों और वस्तुओं पर बाहरी प्रभाव, और प्रकाश और ध्वनि संकेतों के प्रति मानव प्रतिक्रिया में देरी शामिल हैं। . उनकी अभिव्यक्ति की प्रकृति के आधार पर, त्रुटियों को व्यवस्थित और यादृच्छिक में विभाजित किया जाता है। एक यादृच्छिक घटना एक ऐसी घटना है, जो कारकों के दिए गए सेट को देखते हुए घटित हो भी सकती है और नहीं भी। यादृच्छिक त्रुटि माप त्रुटि का एक घटक है जो एक ही मात्रा के बार-बार माप के साथ यादृच्छिक रूप से बदलता है। यादृच्छिक त्रुटियों की एक विशिष्ट विशेषता निरंतर माप स्थितियों के तहत त्रुटि के परिमाण और संकेत में परिवर्तन है। व्यवस्थित त्रुटि माप त्रुटि का एक घटक है जो स्थिर रहता है या एक ही मात्रा के बार-बार माप के साथ स्वाभाविक रूप से बदलता है। व्यवस्थित त्रुटियों को, सैद्धांतिक रूप से, सुधार और अधिक सटीक उपकरणों और विधियों के उपयोग के माध्यम से समाप्त किया जा सकता है (हालांकि व्यवहार में व्यवस्थित त्रुटियों का पता लगाना हमेशा आसान नहीं होता है)। व्यक्तिगत माप में यादृच्छिक त्रुटियों को बाहर करना असंभव है; यादृच्छिक घटनाओं का गणितीय सिद्धांत (संभावना सिद्धांत) केवल उनके परिमाण का उचित अनुमान स्थापित करने की अनुमति देता है। आइए मान लें कि व्यवस्थित त्रुटियों को बाहर रखा गया है और माप परिणामों में त्रुटियां केवल यादृच्छिक हैं। आइए हम किसी भौतिक मात्रा के माप के परिणामों को अक्षरों से निरूपित करें, जिसका वास्तविक मान बराबर है समानता (1) के बाएँ और दाएँ पक्षों को सारांशित करने पर, हम प्राप्त करते हैं: यादृच्छिक त्रुटियों का सिद्धांत अनुभव द्वारा पुष्टि की गई मान्यताओं पर आधारित है: त्रुटियाँ मानों की एक सतत श्रृंखला पर आधारित हो सकती हैं; बड़ी संख्या में मापों के साथ, समान परिमाण की, लेकिन विभिन्न संकेतों की यादृच्छिक त्रुटियां, समान रूप से अक्सर होती हैं; जैसे-जैसे इसका परिमाण बढ़ता है, त्रुटि की संभावना कम हो जाती है। यह भी आवश्यक है कि त्रुटियाँ मापे गए मान की तुलना में छोटी और स्वतंत्र हों। धारणा (1) के अनुसार, माप की संख्या n के साथ हम प्राप्त करते हैं हालाँकि, आयामों की संख्या हमेशा सीमित होती है संभाव्यता सिद्धांत के अनुसार, मापों की एक श्रृंखला का अंकगणितीय माध्य यह प्रायिकता कि वांछित मान (इसका वास्तविक मान) अंतराल (a - a, a + a) में निहित है, को आत्मविश्वास संभाव्यता (विश्वसनीयता) कहा जाएगा, और संगत अंतराल (a - a, a +) कहा जाएगा ए) - आत्मविश्वास अंतराल; त्रुटि a जितनी छोटी होगी, मापी गई मान इस त्रुटि द्वारा परिभाषित अंतराल में समाहित होने की संभावना उतनी ही कम होगी। विपरीत कथन भी सत्य है: परिणाम जितना कम विश्वसनीय होगा, वांछित मूल्य का विश्वास अंतराल उतना ही कम होगा। बड़े n के लिए (व्यावहारिक रूप से n 100 के लिए), किसी दिए गए विश्वसनीयता के लिए विश्वास अंतराल की आधी-चौड़ाई के बराबर है जहां K() = 1 पर = 0.68; K() = 2 पर = 0.95; K() = 3 पर = 0.997. माप की एक छोटी संख्या के साथ, जो अक्सर छात्र प्रयोगशाला अभ्यास में पाया जाता है, (3) में गुणांक K() न केवल पर निर्भर करता है, बल्कि माप n की संख्या पर भी निर्भर करता है। इसलिए, केवल एक यादृच्छिक त्रुटि की उपस्थिति में, हम हमेशा सूत्र का उपयोग करके विश्वास अंतराल की आधी-चौड़ाई पाएंगे (4) में, गुणांक t n को छात्र गुणांक कहा जाता है। छात्र व्यावहारिक कार्य में अपनाए गए = 0.95 के लिए, t n के मान इस प्रकार हैं: मान को मापों की श्रृंखला के अंकगणितीय माध्य की मूल-माध्य-वर्ग त्रुटि कहा जाता है। किसी उपकरण या माप की त्रुटि आमतौर पर उसके पासपोर्ट में या उपकरण पैमाने पर एक प्रतीक द्वारा इंगित की जाती है। आमतौर पर, उपकरण त्रुटि को अंतराल की आधी-चौड़ाई के रूप में समझा जाता है जिसके भीतर मापा मूल्य 0.997 की माप संभावना के साथ समाहित किया जा सकता है, यदि माप त्रुटि केवल उपकरण त्रुटि के कारण होती है। माप परिणाम की सामान्य (कुल) त्रुटि के रूप में, हम प्रायिकता = 0.95 के साथ स्वीकार करेंगे पूर्ण त्रुटि आपको यह निर्धारित करने की अनुमति देती है कि प्राप्त परिणाम के किस संकेत में अशुद्धि निहित है। सापेक्ष त्रुटि यह जानकारी देती है कि मापे गए मान का कौन सा अनुपात (प्रतिशत) त्रुटि (विश्वास अंतराल की आधी-चौड़ाई) है। हम मान a 0 के प्रत्यक्ष मापों की श्रृंखला का अंतिम परिणाम फॉर्म में लिखते हैं उदाहरण के लिए इस प्रकार, प्रयोगात्मक रूप से पाई गई किसी भी भौतिक मात्रा का प्रतिनिधित्व किया जाना चाहिए: आयाम कहलाते हैं सीधा,यदि मात्राओं का मान सीधे उपकरणों द्वारा निर्धारित किया जाता है (उदाहरण के लिए, रूलर से लंबाई मापना, स्टॉपवॉच से समय निर्धारित करना, आदि)। आयाम कहलाते हैं अप्रत्यक्ष, यदि मापी गई मात्रा का मूल्य अन्य मात्राओं के प्रत्यक्ष माप के माध्यम से निर्धारित किया जाता है जो मापे जा रहे विशिष्ट संबंध से जुड़े होते हैं। निरपेक्ष और सापेक्ष त्रुटि.इसे क्रियान्वित किया जाये एनएक ही मात्रा का माप एक्सव्यवस्थित त्रुटि के अभाव में. व्यक्तिगत माप परिणाम इस प्रकार हैं: एक्स 1
,एक्स 2
,
…,एक्स एन. मापे गए मान का औसत मान सर्वोत्तम के रूप में चुना गया है: पूर्ण त्रुटिएकल माप के रूप का अंतर कहा जाता है: औसत निरपेक्ष त्रुटि एनइकाई माप: बुलाया औसत निरपेक्ष त्रुटि. रिश्तेदारों की गलतीमापी गई मात्रा के औसत मान से औसत निरपेक्ष त्रुटि का अनुपात कहलाता है: यदि कोई विशेष निर्देश नहीं हैं, तो उपकरण त्रुटि उसके विभाजन मूल्य (रूलर, बीकर) के आधे के बराबर है। वर्नियर से सुसज्जित उपकरणों की त्रुटि वर्नियर डिवीजन (माइक्रोमीटर - 0.01 मिमी, कैलीपर - 0.1 मिमी) के मूल्य के बराबर है। तालिका मानों की त्रुटि अंतिम अंक की आधी इकाई (अंतिम महत्वपूर्ण अंक के बाद अगले क्रम की पाँच इकाइयाँ) के बराबर है। विद्युत माप उपकरणों की त्रुटि की गणना सटीकता वर्ग के अनुसार की जाती है साथउपकरण पैमाने पर दर्शाया गया है: उदाहरण के लिए: कहाँ यू अधिकतमऔर मैं अधिकतम- डिवाइस की माप सीमा. डिजिटल डिस्प्ले वाले उपकरणों की त्रुटि डिस्प्ले के अंतिम अंक में से एक के बराबर होती है। यादृच्छिक और वाद्य त्रुटियों का आकलन करने के बाद, जिसका मूल्य अधिक होता है, उसे ध्यान में रखा जाता है। अधिकांश माप अप्रत्यक्ष हैं। इस मामले में, वांछित मान X कई चरों का एक फ़ंक्शन है ए,बी,
सी…
, जिसका मान प्रत्यक्ष माप द्वारा पाया जा सकता है: X = f( ए,
बी,
सी…). अप्रत्यक्ष माप के परिणाम का अंकगणितीय माध्य इसके बराबर होगा: एक्स = एफ( ए, बी, सी…). त्रुटि की गणना करने का एक तरीका फ़ंक्शन X = f( के प्राकृतिक लघुगणक को अलग करना है ए,
बी,
सी...) यदि, उदाहरण के लिए, वांछित मान X संबंध X = द्वारा निर्धारित किया जाता है इस अभिव्यक्ति का अंतर इस प्रकार है: अनुमानित मानों की गणना के संबंध में सापेक्ष त्रुटि के लिए इसे इस प्रकार लिखा जा सकता है: =
पूर्ण त्रुटि की गणना सूत्र का उपयोग करके की जाती है: Х = Х(5) इस प्रकार, त्रुटियों की गणना और अप्रत्यक्ष माप के परिणाम की गणना निम्नलिखित क्रम में की जाती है: 1) अंतिम परिणाम की गणना के लिए प्रारंभिक सूत्र में शामिल सभी मात्राओं को मापें। 2) प्रत्येक मापे गए मान के अंकगणितीय औसत मान और उनकी पूर्ण त्रुटियों की गणना करें। 3) सभी मापे गए मानों के औसत मानों को मूल सूत्र में रखें और वांछित मान के औसत मान की गणना करें: एक्स = एफ( ए, बी, सी…). 4) मूल सूत्र का लघुगणक X = f( ए,
बी,
सी...) और सापेक्ष त्रुटि के लिए सूत्र (4) के रूप में अभिव्यक्ति लिखें। 5) सापेक्ष त्रुटि की गणना करें = 6) सूत्र (5) का उपयोग करके परिणाम की पूर्ण त्रुटि की गणना करें। 7) अंतिम परिणाम इस प्रकार लिखा गया है: एक्स = एक्स औसत एक्स सरलतम कार्यों की पूर्ण और सापेक्ष त्रुटियाँ तालिका में दी गई हैं: निरपेक्ष गलती रिश्तेदार गलती ए+
बी ए+
बी व्यवस्थित त्रुटियाँ. व्यवस्थित त्रुटियाँ स्वाभाविक रूप से मापी गई मात्रा के मूल्यों को बदल देती हैं। उपकरणों द्वारा माप में की गई त्रुटियों का आकलन सबसे आसानी से किया जा सकता है यदि वे स्वयं उपकरणों की डिज़ाइन सुविधाओं से जुड़े हों। इन त्रुटियों को उपकरणों के पासपोर्ट में दर्शाया गया है। डेटा शीट का संदर्भ दिए बिना कुछ उपकरणों की त्रुटियों का आकलन किया जा सकता है। कई विद्युत माप उपकरणों के लिए, सटीकता वर्ग को सीधे पैमाने पर इंगित किया जाता है। उपकरण सटीकता वर्ग- यह डिवाइस की पूर्ण त्रुटि और मापी गई मात्रा के अधिकतम मूल्य का अनुपात है, जिसे इस डिवाइस का उपयोग करके निर्धारित किया जा सकता है (यह इस डिवाइस की व्यवस्थित सापेक्ष त्रुटि है, जिसे स्केल रेटिंग के प्रतिशत के रूप में व्यक्त किया गया है)। तब ऐसे उपकरण की पूर्ण त्रुटि संबंध द्वारा निर्धारित की जाती है: विद्युत माप उपकरणों के लिए, 8 सटीकता वर्ग पेश किए गए हैं: 0.05; 0.1; 0.5; 1.0; 1.5; 2.0; 2.5; 4. मापा गया मान नाममात्र मान के जितना करीब होगा, माप परिणाम उतना ही अधिक सटीक होगा। किसी दिए गए उपकरण द्वारा प्रदान की जा सकने वाली अधिकतम सटीकता (यानी, सबसे छोटी सापेक्ष त्रुटि) सटीकता वर्ग के बराबर होती है। मल्टीस्केल उपकरणों का उपयोग करते समय इस परिस्थिति को ध्यान में रखा जाना चाहिए। पैमाने का चयन इस तरह से किया जाना चाहिए कि मापा मूल्य, पैमाने के भीतर रहते हुए, नाममात्र मूल्य के जितना संभव हो उतना करीब हो। यदि डिवाइस के लिए सटीकता वर्ग निर्दिष्ट नहीं है, तो निम्नलिखित नियमों का पालन किया जाना चाहिए: · वर्नियर वाले उपकरणों की पूर्ण त्रुटि वर्नियर की सटीकता के बराबर होती है। · एक निश्चित तीर पिच वाले उपकरणों की पूर्ण त्रुटि विभाजन मान के बराबर है। · डिजिटल उपकरणों की पूर्ण त्रुटि एक न्यूनतम अंक के बराबर है। · अन्य सभी उपकरणों के लिए, पूर्ण त्रुटि आधे विभाजन मान के बराबर मानी जाती है। यादृच्छिक त्रुटियाँ. ये त्रुटियाँ प्रकृति में सांख्यिकीय हैं और संभाव्यता सिद्धांत द्वारा वर्णित हैं। यह स्थापित किया गया है कि बहुत बड़ी संख्या में मापों के साथ, प्रत्येक व्यक्तिगत माप में एक या दूसरे परिणाम प्राप्त करने की संभावना गाऊसी सामान्य वितरण का उपयोग करके निर्धारित की जा सकती है। माप की एक छोटी संख्या के साथ, एक या दूसरे माप परिणाम प्राप्त करने की संभावना के गणितीय विवरण को छात्र वितरण कहा जाता है (आप इसके बारे में आई.एल. स्कोवर्त्सोवा के मैनुअल "भौतिक मात्रा में माप त्रुटियां" में अधिक पढ़ सकते हैं)। मापी गई मात्रा के सही मूल्य का मूल्यांकन कैसे करें? मान लीजिए कि एक निश्चित मान मापते समय हमें N परिणाम प्राप्त हुए: 1). परिकलित औसतएन प्रत्यक्ष माप की श्रृंखला: 2). परिकलित प्रत्येक माप की पूर्ण यादृच्छिक त्रुटिएन प्रत्यक्ष माप की एक श्रृंखला और इस माप के अंकगणितीय माध्य के बीच का अंतर है: 3). परिकलित माध्य वर्ग निरपेक्ष त्रुटि: 4). परिकलित पूर्ण यादृच्छिक त्रुटि. माप की एक छोटी संख्या के साथ, पूर्ण यादृच्छिक त्रुटि की गणना माध्य वर्ग त्रुटि और एक निश्चित गुणांक के माध्यम से की जा सकती है जिसे छात्र गुणांक कहा जाता है: छात्र गुणांक माप की संख्या एन और विश्वसनीयता गुणांक पर निर्भर करता है (तालिका 1 विश्वसनीयता गुणांक के एक निश्चित मूल्य पर माप की संख्या पर छात्र गुणांक की निर्भरता दिखाता है)। विश्वसनीयता कारकवह संभावना है जिसके साथ मापे गए मूल्य का सही मूल्य विश्वास अंतराल के भीतर आता है। विश्वास अंतराल इस प्रकार, छात्र गुणांक वह संख्या है जिससे किसी दिए गए माप के परिणाम की निर्दिष्ट विश्वसनीयता सुनिश्चित करने के लिए माध्य वर्ग त्रुटि को गुणा किया जाना चाहिए। माप की दी गई संख्या के लिए जितनी अधिक विश्वसनीयता की आवश्यकता होगी, छात्र गुणांक उतना ही अधिक होगा। दूसरी ओर, माप की संख्या जितनी अधिक होगी, किसी दी गई विश्वसनीयता के लिए छात्र गुणांक उतना ही कम होगा। हमारी कार्यशाला के प्रयोगशाला कार्य में, हम मान लेंगे कि विश्वसनीयता दी गई है और 0.9 के बराबर है। माप की विभिन्न संख्याओं के लिए इस विश्वसनीयता के लिए छात्र के गुणांक के संख्यात्मक मान तालिका 1 में दिए गए हैं। तालिका नंबर एक 5).गणना कुल निरपेक्ष त्रुटि.किसी भी माप में यादृच्छिक और व्यवस्थित दोनों प्रकार की त्रुटियाँ होती हैं। कुल (कुल) निरपेक्ष माप त्रुटि की गणना करना कोई आसान काम नहीं है, क्योंकि ये त्रुटियाँ अलग-अलग प्रकृति की होती हैं। इंजीनियरिंग माप के लिए, व्यवस्थित और यादृच्छिक निरपेक्ष त्रुटियों को संक्षेप में प्रस्तुत करना समझ में आता है गणना की सरलता के लिए, कुल निरपेक्ष त्रुटि का अनुमान पूर्ण यादृच्छिक और पूर्ण व्यवस्थित (वाद्य) त्रुटियों के योग के रूप में लगाने की प्रथा है, यदि त्रुटियाँ परिमाण के समान क्रम की हैं, और यदि त्रुटियाँ हैं तो उनमें से किसी एक की उपेक्षा करना प्रथागत है। परिमाण के एक क्रम से अधिक (10 गुना) दूसरे से कम। 6). त्रुटि और परिणाम पूर्णांकित हैं. चूँकि माप परिणाम को मानों के अंतराल के रूप में प्रस्तुत किया जाता है, जिसका मान कुल निरपेक्ष त्रुटि से निर्धारित होता है, परिणाम और त्रुटि का सही पूर्णांकन महत्वपूर्ण है। पूर्णांकन पूर्ण त्रुटि से प्रारंभ होता है!!!त्रुटि मान में छोड़े गए महत्वपूर्ण अंकों की संख्या, आम तौर पर बोलना, विश्वसनीयता गुणांक और माप की संख्या पर निर्भर करती है। हालाँकि, बहुत सटीक माप (उदाहरण के लिए, खगोलीय) के लिए भी, जिसमें त्रुटि का सटीक मान महत्वपूर्ण है, दो से अधिक महत्वपूर्ण आंकड़े न छोड़ें। बड़ी संख्या में संख्याओं का कोई मतलब नहीं है, क्योंकि त्रुटि की परिभाषा की अपनी त्रुटि होती है। हमारे अभ्यास में अपेक्षाकृत कम विश्वसनीयता गुणांक और माप की एक छोटी संख्या है। इसलिए, जब (अतिरिक्त के साथ) पूर्णांकन किया जाता है, तो कुल पूर्ण त्रुटि एक महत्वपूर्ण अंक पर छोड़ दी जाती है। पूर्ण त्रुटि के महत्वपूर्ण अंक का अंक परिणाम मान में पहले संदिग्ध अंक का अंक निर्धारित करता है। नतीजतन, परिणाम का मान स्वयं उस महत्वपूर्ण अंक तक पूर्णांकित किया जाना चाहिए (सुधार के साथ) जिसका अंक त्रुटि के महत्वपूर्ण अंक के अंक से मेल खाता है। तैयार किया गया नियम उन मामलों में भी लागू किया जाना चाहिए जहां कुछ संख्याएं शून्य हैं। यदि शरीर का वजन मापते समय प्राप्त परिणाम है, तो संख्या 0.900 के अंत में शून्य लिखना आवश्यक है। रिकॉर्डिंग का मतलब यह होगा कि अगले महत्वपूर्ण आंकड़ों के बारे में कुछ भी नहीं पता था, जबकि माप से पता चला कि वे शून्य थे। 7). परिकलित रिश्तेदारों की गलती . सापेक्ष त्रुटि को पूर्णांकित करते समय, दो महत्वपूर्ण अंक छोड़ना पर्याप्त है। एक निश्चित भौतिक मात्रा के माप की एक श्रृंखला का परिणाम मूल्यों के अंतराल के रूप में प्रस्तुत किया जाता है, जो इस अंतराल में आने वाले वास्तविक मूल्य की संभावना को दर्शाता है, अर्थात, परिणाम को इस रूप में लिखा जाना चाहिए: यहां कुल निरपेक्ष त्रुटि है, जिसे पहले महत्वपूर्ण अंक तक पूर्णांकित किया गया है, और मापा मूल्य का औसत मूल्य है, जिसे पहले से ही पूर्णांकित त्रुटि को ध्यान में रखते हुए पूर्णांकित किया गया है। माप परिणाम रिकॉर्ड करते समय, आपको मूल्य की माप की इकाई को इंगित करना होगा। आइए कुछ उदाहरण देखें: 1. मान लीजिए कि किसी खंड की लंबाई मापते समय, हमें निम्नलिखित परिणाम प्राप्त हुए: सेमी और सेमी। किसी खंड की लंबाई मापने के परिणाम को सही ढंग से कैसे लिखें? सबसे पहले, हम पूर्ण त्रुटि को आधिक्य के साथ पूर्णांकित करते हैं, एक महत्वपूर्ण अंक छोड़ते हैं, देखें। सौवें स्थान पर त्रुटि का महत्वपूर्ण अंक। फिर हम संशोधित औसत मान को निकटतम सौवें तक पूर्णांकित करते हैं, अर्थात। उस सार्थक अंक तक जिसका अंक त्रुटि के सार्थक अंक के अंक से मेल खाता है 
![]() एमीटर के लिए
एमीटर के लिए ![]()
 ,
,![]()
![]() , कहाँ के, एल, एम‒ कोई भी वास्तविक संख्या, तो आपको पहले खोजना होगा रिश्तेदारगलती
, कहाँ के, एल, एम‒ कोई भी वास्तविक संख्या, तो आपको पहले खोजना होगा रिश्तेदारगलती
![]() .
.![]() .
.![]() जे।
जे।नहीं। डी मैं, मिमी
डी मैं-
(डी मैं-
) 2
एच मैं, मिमीऔर

 , (21)
, (21)![]()
![]() , इकाइयाँ परिवर्तन
, इकाइयाँ परिवर्तनप्रत्यक्ष माप की त्रुटियाँ
![]() . व्यक्तिगत माप के परिणामों की पूर्ण त्रुटियाँ इंगित की गई हैं:
. व्यक्तिगत माप के परिणामों की पूर्ण त्रुटियाँ इंगित की गई हैं: (2)
(2)
 ,
,![]() अज्ञात रहता है. लेकिन व्यावहारिक उद्देश्यों के लिए, प्रयोगात्मक रूप से किसी भौतिक मात्रा का मूल्य सत्य के इतना करीब खोजना पर्याप्त है
अज्ञात रहता है. लेकिन व्यावहारिक उद्देश्यों के लिए, प्रयोगात्मक रूप से किसी भौतिक मात्रा का मूल्य सत्य के इतना करीब खोजना पर्याप्त है  सत्य के स्थान पर उपयोग किया जा सकता है। सवाल यह है कि इस सन्निकटन की डिग्री का मूल्यांकन कैसे किया जाए?
सत्य के स्थान पर उपयोग किया जा सकता है। सवाल यह है कि इस सन्निकटन की डिग्री का मूल्यांकन कैसे किया जाए? व्यक्तिगत माप के परिणामों की तुलना में अधिक विश्वसनीय, क्योंकि विभिन्न दिशाओं में वास्तविक मान से यादृच्छिक विचलन समान रूप से संभावित हैं। चौड़ाई 2a i के अंतराल में किसी मान a i के प्रकट होने की संभावना को अंतराल 2a i के भीतर आने वाले a i के मानों के घटित होने की सापेक्ष आवृत्ति के रूप में समझा जाता है, जो कि i के सभी प्रकट मानों की संख्या के बराबर है। प्रयोगों (माप) की संख्या अनंत की ओर बढ़ रही है। जाहिर है, एक विश्वसनीय घटना की संभावना एक के बराबर है, एक असंभव घटना की संभावना शून्य के बराबर है, अर्थात। 0 100%।
व्यक्तिगत माप के परिणामों की तुलना में अधिक विश्वसनीय, क्योंकि विभिन्न दिशाओं में वास्तविक मान से यादृच्छिक विचलन समान रूप से संभावित हैं। चौड़ाई 2a i के अंतराल में किसी मान a i के प्रकट होने की संभावना को अंतराल 2a i के भीतर आने वाले a i के मानों के घटित होने की सापेक्ष आवृत्ति के रूप में समझा जाता है, जो कि i के सभी प्रकट मानों की संख्या के बराबर है। प्रयोगों (माप) की संख्या अनंत की ओर बढ़ रही है। जाहिर है, एक विश्वसनीय घटना की संभावना एक के बराबर है, एक असंभव घटना की संभावना शून्य के बराबर है, अर्थात। 0 100%। ,
(3)
,
(3) (4)
(4)
 .
. (6)
(6)
प्रत्यक्ष माप में यादृच्छिक त्रुटियाँ
 .
. (2)
(2) .
(3)
.
(3)प्रत्यक्ष माप में उपकरण त्रुटियाँ
 और
और  ,
,अप्रत्यक्ष माप में त्रुटियों की गणना
 , तो लघुगणक के बाद हमें मिलता है: lnX = ln ए+एल.एन बी+एलएन( सी+
डी).
, तो लघुगणक के बाद हमें मिलता है: lnX = ln ए+एल.एन बी+एलएन( सी+
डी). .
. .
(4)
.
(4) .
.


![]() .
.![]() . मापों की एक श्रृंखला का अंकगणितीय माध्य अधिकांश व्यक्तिगत मापों की तुलना में मापी गई मात्रा के वास्तविक मूल्य के करीब है। एक निश्चित मान को मापने का परिणाम प्राप्त करने के लिए, निम्नलिखित एल्गोरिदम का उपयोग किया जाता है।
. मापों की एक श्रृंखला का अंकगणितीय माध्य अधिकांश व्यक्तिगत मापों की तुलना में मापी गई मात्रा के वास्तविक मूल्य के करीब है। एक निश्चित मान को मापने का परिणाम प्राप्त करने के लिए, निम्नलिखित एल्गोरिदम का उपयोग किया जाता है।![]() .
. .
.![]() ,
,![]() एक संख्यात्मक अंतराल है जिसमें मापी गई मात्रा का वास्तविक मूल्य एक निश्चित संभावना के साथ आता है।
एक संख्यात्मक अंतराल है जिसमें मापी गई मात्रा का वास्तविक मूल्य एक निश्चित संभावना के साथ आता है।![]() .
.![]() सापेक्ष त्रुटि की गणना करें देखें
सापेक्ष त्रुटि की गणना करें देखें