Open Library: una biblioteca aperta di informazioni educative. Albero pitagorico esposto al vento Utilizzo di una procedura ricorsiva per costruire la figura di un albero pitagorico

L'albero di Pitagora è un tipo di frattale basato su una figura conosciuta come Pantaloni Pitagorici.

Dimostrando il suo famoso teorema, Pitagora costruì una figura in cui su ciascun lato di un triangolo rettangolo c'erano dei quadrati. Nel tempo, questa figura di Pitagora si trasformò in un intero albero. Il primo a costruire l'albero di Pitagora durante la Seconda Guerra Mondiale fu A. Bosman, utilizzando un normale righello da disegno.

Una delle proprietà principali dell'albero di Pitagora è che quando l'area del primo quadrato è uno, ad ogni livello anche la somma delle aree dei quadrati sarà uguale a uno. L'albero pitagorico classico ha un angolo di 45 gradi, ma è anche possibile costruire un albero pitagorico generalizzato utilizzando altri angoli. Un albero del genere è chiamato l’albero portato dal vento di Pitagora. Se disegni solo i segmenti che in qualche modo collegano alcuni “centri” dei triangoli, otterrai un albero pitagorico nudo.

Un altro esempio potrebbe essere il famoso "albero pitagorico". Viene spesso rappresentato come in Fig. 3.2. Ciascuno dei triangoli rettangoli di questo albero ha un angolo interno di 45°.

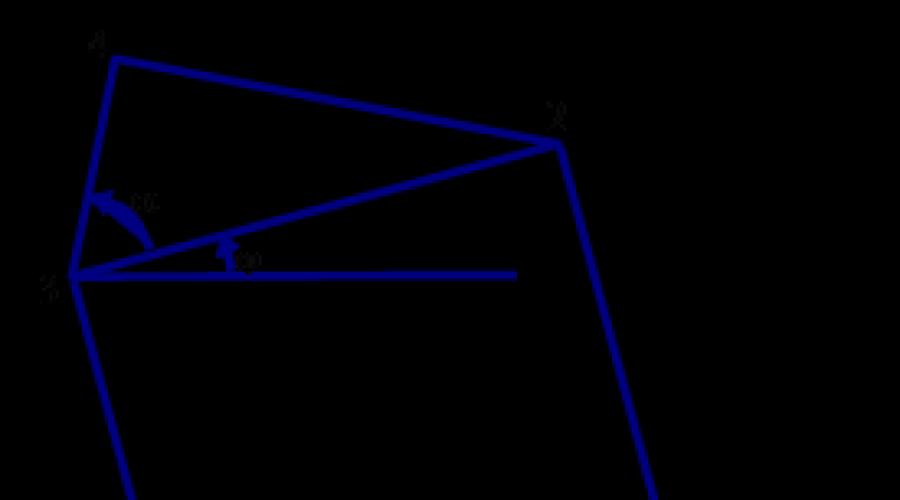
Ancora una volta, utilizzeremo un generatore di numeri casuali per creare un programma più generale in grado di generare non solo riso. 3.2, ma generano anche alberi meno regolari. Angoli impostati a 45° per Fig. 3.2, in generale, verrà impostato in modo casuale nell'intervallo compreso tra (45 - delta)° e (45+ delta)° , dov'è il valore delta viene fornito come parametro di input insieme al parametro n, che determina la profondità di ricorsione. La versione normale mostrata in Fig. 3.2, ottenuto specificando delta= 0 en = 7. Nella figura, il parametro P determina il numero di triangoli sul percorso dalla radice alle foglie dell'albero. Il nucleo del programma sarà la funzione ricorsiva quadrato_e_triangolo ("quadrato e triangolo") con il parametro n, che determina la profondità della ricorsione, come primo argomento. Se il valore del parametro n è maggiore di zero, allora la funzione quadrato_e_triangolo, come suggerisce il nome, disegnerà sopra un quadrato e un triangolo, e poi si chiamerà altre due volte con i nuovi argomenti corrispondenti, il primo dei quali è impostato su n-1. La dimensione e la posizione del quadrato sono completamente determinate da quattro parametri: X0, Y0, aeb (vedi Fig. 3.3). Per disegnare un triangolo, devi conoscere l'angolo a. Questo angolo, espresso in gradi, è pari a 45+deviazione, dove la deviazione è pari a uno dei numeri interi della serie -delta, -delta+I, ... , delta, scelto a caso. Nella fig. 3.3 i punti necessari sono numerati con i numeri consecutivi 0,1,2,3,4. Le coordinate X0, Y0 del punto O vengono specificate in una chiamata alla funzione. Per calcolare i punti rimanenti consideriamo innanzitutto una situazione più semplice con j = 0, ovvero quando il lato 0 1 del quadrato occupa una posizione orizzontale.

In questa posizione, le coordinate dei punti sono molto facili da determinare. Sono memorizzati negli array xey. Quindi l'intera struttura viene ruotata attorno al punto O dell'angolo j. Il risultato della rotazione viene registrato negli array xx e yy.

/* PYTH_TREE: variante dell'albero pitagorico */

#include "matematica.h"

#include "stdlib.h"

#include "ora.h"

#define pi greco 3.1415927

#include "stdio.h"

struct (float xx; float yy; int ii;) s;

void pfopen())( fp=fopen("scratch", "wb"); )

void pmove(float x,float y)

( s.xx=x; s.yy=y; s.ii=0; /* 0 = penna su */ /* 0 = penna su */

fwrite(&s, sizeof s, 1, fp);

void pdraw(float x,float y)

( s.xx=x; s.yy=y; s.ii=1; /* 1 = penna abbassata */ /* 1 = penna abbassata */

fwrite(&s, sizeof s, 1, fp);

void pfclose())( fclose(fp); )

void quadrato_e_triangolo(int n,float x0,float y0, float a, float phi)

( float x, y, xx, yy, cphi, sphi, c1, c2, b, c,

alfa, calfa, salfa;

int i, deviazione; /* phi e alfa in radianti */

/* delta in gradi */

se(n==0) ritorno; /* angoli phi e alfa in radianti */

/* delta dell'angolo in gradi */

deviazione=rand()%(2*delta+1)-delta;

alfa=(45+deviazione)*pi/180.0;

x=x=x0; x=x=x0+a;

y=y=y0; y=y=y0+a;

calpha=cos(alfa); salfa=peccato(alfa);

c=a*calfa; b=a*alfa;

/* Rotazione attorno a (x0, y0) attraverso l'angolo phi ; */

/* Ruota attorno al punto (x0, y0) dell'angolo phi;*/

cphi=cos(phi); sphi=peccato(phi);

c1=x0-x0*cphi+y0*sphi;

c2=y0-x0*sphi-y0*cphi;

per (i=0; i<5; i++)

( xx[i]=x[i]*cphi-y[i]*sphi+c1;

aa[i]=x[i]*sphi+y[i]*cphi+c2;

per (i=0; i<5; i++) pdraw(xx[i],yy[i]);

quadrato_e_triangolo(n-1, xx, yy, c, phi+alfa);

quadrato_e_triangolo(n-1, xx, yy, b, phi+alfa-0,5*pi);

pfopen(); tempo(&seme); srand((int)seme);

printf(" Imposta l'angolo delta in gradi (0< delta < 45) ");

scanf("%d", &delta);

printf("Imposta profondità di ricorsione n"); scanf("%d", &n);

quadrato_e_triangolo(n, 0.0, 0.0, 1.0, 0.0);

Questo programma genera un file GRAFFIO che deve essere elaborato dal programma G ENPLOT dalla lezione 2. Risultato grafico del programma per delta= 30 e n = 7 è mostrato in Fig. 3.4.

L'albero di Pitagora è un tipo di frattale basato su una figura conosciuta come Pantaloni Pitagorici.

Dimostrando il suo famoso teorema, Pitagora costruì una figura in cui su ciascun lato di un triangolo rettangolo c'erano dei quadrati. Nel tempo, questa figura di Pitagora si trasformò in un intero albero. Il primo a costruire l'albero di Pitagora durante la Seconda Guerra Mondiale fu A. Bosman, utilizzando un normale righello da disegno.

Una delle proprietà principali dell'albero di Pitagora è che quando l'area del primo quadrato è uno, ad ogni livello anche la somma delle aree dei quadrati sarà uguale a uno. L'albero pitagorico classico ha un angolo di 45 gradi, ma è anche possibile costruire un albero pitagorico generalizzato utilizzando altri angoli. Un albero del genere è chiamato l’albero portato dal vento di Pitagora. Se disegni solo i segmenti che in qualche modo collegano alcuni “centri” dei triangoli, otterrai un albero pitagorico nudo.

L'insieme di Mandelbrot è un classico esempio di frattale... Wikipedia

HTML HTML e HTML5 HTML dinamico ... Wikipedia

L'insieme di Mandelbrot è un classico esempio di frattale.Frattale (lat. fractus schiacciato) è un termine che indica una figura geometrica che ha la proprietà di autosimilarità, cioè composta da più parti, ciascuna delle quali è simile all'intero figura... ... Wikipedia

Frattale della curva di prelievo. Proposto dal matematico francese P. Levy. Si scopre se prendi mezzo quadrato della forma /, quindi sostituisci ciascun lato con lo stesso frammento e, ripetendo questa operazione, in ... Wikipedia

Piscine di Newton...Wikipedia

Il grafico di Cayley è un grafico costruito da un gruppo con un sistema distinto di generatori. Prende il nome da Caylee. Definizione Sia dato un gruppo discreto G e un sistema di generatori S. Supponiamo S = S − 1, cioè per ciascuno. Conteggio Cayley del gruppo G secondo il sistema... ... Wikipedia

Un grafico costruito da un gruppo con un sistema dedicato di generatori. Prende il nome da Caylee. Definizione Sia dato un gruppo discreto e un sistema di generatori. Supponiamo, cioè, per ciascuno. Gruppo del conte Cayley ... Wikipedia

Antica religione iraniana nelle fonti antiche. L'articolo contiene una revisione delle informazioni di autori antichi (greco antico, latino e in parte armeno e siriano) del V secolo a.C. e. VI secolo d.C e. sulla religione dei popoli iranici di epoca achemenide, i Parti e il potere... Wikipedia

La cultura dei popoli che l'abitarono nell'antichità, nel IV-I millennio a.C. e., Mesopotamia Mesopotamia Tigri ed Eufrate (il territorio del moderno Iraq), Sumeri e Accadi, Babilonesi e Assiri, che crearono i grandi stati di Sumer, Akkad, Babilonia (Vedi... ... Grande Enciclopedia Sovietica

Libri

• Alla fine dell'estate, Vera Orlovskaya. Il nuovo libro di Vera Orlovskaya ALLA FINE DELL'ESTATE continua a stupire il lettore con la sua varietà di forme e ciò che alcuni titoli suggeriscono: LA FILOSOFIA DI PITAGORO IN NUMERI, L'ALBERO DEL SOGNO, SINFONIA N. 1...
• R-funziona come dispositivo nelle applicazioni della geometria frattale, A. V. Tolok. L'apparato matematico della teoria delle funzioni R viene utilizzato per descrivere oggetti della geometria frattale mediante le funzioni ɷ(x) = 0, x ∈ En, dove ɷ(x) ha la forma di un'unica espressione analitica. Di…

Ciao, amici interessati ai frattali e altro ancora. A partire da questo momento lancio una serie di post in cui spiegherò i principi per costruire i frattali più semplici. È sempre interessante studiare e io ti aiuterò in questo: d'ora in poi conosceremo tanti, tanti frattali. L'attrattore di Lorenz nell'articolo sul caos ne è un esempio. E oggi vi parlerò dell'albero pitagorico.

Quindi, cos'è? L'albero di Pitagora è il frattale più semplice che si possa disegnare su carta. Ma perché questo frattale si chiama albero pitagorico? Il fatto è che qui esiste una connessione con il teorema di Pitagora, uno dei fondamenti della geometria euclidea. La ricordi? Ti ricordo: a2 + b2 = c2 (la somma dei quadrati delle lunghezze dei cateti è uguale al quadrato della lunghezza dell'ipotenusa). Questo teorema è noto fin dall'antichità; attualmente esistono più di 400 dimostrazioni del teorema, e solo Pitagora fu il primo a dimostrarlo geometricamente. Costruì la seguente figura: prese un triangolo rettangolo e disegnò dei quadrati sui suoi lati. Questa figura è anche chiamata “pantaloni pitagorici”:

Se continuiamo questa costruzione ricorsivamente, ci ritroveremo con un albero pitagorico:
1a iterazione (nel nostro albero pitagorico l'angolo è 45 gradi):

Seconda iterazione:

Terza iterazione:

Decima iterazione:

Una proprietà importante dell'albero pitagorico: se l'area del primo quadrato è uguale a uno, allora ad ogni livello anche la somma delle aree dei quadrati sarà uguale a uno.
Se l'angolo viene modificato da 45 gradi, è possibile costruire altri tipi di albero pitagorico.
Ecco, ad esempio, il cosiddetto “albero di Pitagora mosso dal vento”:

Alcuni generatori di grafica frattale implementano una formula per costruire un frattale basato sull'albero di Pitagora. Questa implementazione ricorda molto il sistema IFS, soprattutto se si sostituiscono i quadrati con rettangoli o forme allungate.
Per oggi è tutto, fino ai prossimi incontri, nei quali ci saranno tanti altri frattali interessanti)