Formula per il calcolo dell'errore relativo. Errori di misura assoluti e relativi
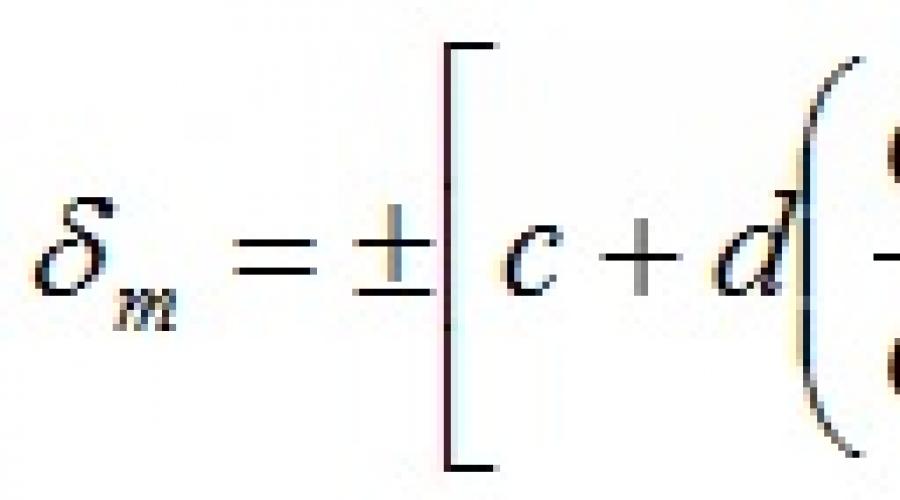
Leggi anche
È quasi impossibile determinare il vero valore di una quantità fisica in modo assolutamente accurato, perché qualsiasi operazione di misurazione è associata a una serie di errori o, in altre parole, imprecisioni. Le ragioni degli errori possono essere molto diverse. Il loro verificarsi può essere associato a imprecisioni nella fabbricazione e nella regolazione del dispositivo di misurazione, a causa delle caratteristiche fisiche dell'oggetto in studio (ad esempio, quando si misura il diametro di un filo di spessore non uniforme, il risultato dipende in modo casuale dal scelta del sito di misurazione), ragioni casuali, ecc.
Il compito dello sperimentatore è ridurre la propria influenza sul risultato e anche indicare quanto il risultato ottenuto è vicino a quello reale.
Esistono concetti di errore assoluto e relativo.
Sotto errore assoluto le misurazioni capiranno la differenza tra il risultato della misurazione e il valore reale della quantità misurata:
∆x i =x i -x e (2)
dove ∆x i è l'errore assoluto della i-esima misurazione, x i _ è il risultato della i-esima misurazione, x ed è il valore vero del valore misurato.
Il risultato di qualsiasi misurazione fisica è solitamente scritto nella forma:
dove è il valore medio aritmetico del valore misurato, più vicino al valore vero (la validità di x e≈ verrà mostrata di seguito), è l'errore di misurazione assoluto.
L'uguaglianza (3) dovrebbe essere intesa in modo tale che il vero valore della quantità misurata si trovi nell'intervallo [ - , + ].
L'errore assoluto è una quantità dimensionale; ha la stessa dimensione della quantità misurata.
L'errore assoluto non caratterizza pienamente l'accuratezza delle misurazioni effettuate. Infatti, se misuriamo segmenti lunghi 1 me 5 mm con lo stesso errore assoluto ± 1 mm, la precisione delle misurazioni sarà incomparabile. Pertanto, insieme all'errore di misurazione assoluto, viene calcolato l'errore relativo.
Errore relativo misurazioni è il rapporto tra l'errore assoluto e il valore misurato stesso:
L'errore relativo è una quantità adimensionale. È espresso in percentuale:
Nell'esempio sopra, gli errori relativi sono 0,1% e 20%. Differiscono notevolmente tra loro, sebbene i valori assoluti siano gli stessi. L'errore relativo fornisce informazioni sulla precisione
Errori di misurazione
In base alla natura della manifestazione e alle ragioni del verificarsi degli errori, questi possono essere suddivisi nelle seguenti classi: strumentali, sistematici, casuali e mancati (errori grossolani).
Gli errori sono causati da un malfunzionamento del dispositivo, o da una violazione della metodologia o delle condizioni sperimentali, oppure sono di natura soggettiva. In pratica, sono definiti come risultati che differiscono nettamente dagli altri. Per eliminare il loro verificarsi, è necessario essere attenti e scrupolosi quando si lavora con i dispositivi. I risultati contenenti errori devono essere esclusi dalla considerazione (scartati).
Errori dello strumento. Se il dispositivo di misurazione è in buone condizioni e regolato, è possibile effettuare misurazioni su di esso con una precisione limitata determinata dal tipo di dispositivo. È consuetudine considerare l'errore strumentale di uno strumento a puntatore pari alla metà della divisione più piccola della sua scala. Negli strumenti con lettura digitale, l'errore dello strumento è equiparato al valore di una cifra più piccola della scala dello strumento.
Gli errori sistematici sono errori la cui grandezza e segno sono costanti per l'intera serie di misurazioni effettuate con lo stesso metodo e utilizzando gli stessi strumenti di misura.
Quando si eseguono misurazioni, è importante non solo tenere conto degli errori sistematici, ma è anche necessario garantirne l'eliminazione.
Gli errori sistematici sono convenzionalmente divisi in quattro gruppi:
1) errori, la cui natura è nota e la cui entità può essere determinata in modo abbastanza accurato. Un tale errore è, ad esempio, una variazione della massa misurata nell'aria, che dipende dalla temperatura, dall'umidità, dalla pressione dell'aria, ecc.;
2) errori di cui è nota la natura, ma non si conosce l'entità dell'errore stesso. Tali errori includono errori causati dal dispositivo di misurazione: un malfunzionamento del dispositivo stesso, una scala che non corrisponde al valore zero o la classe di precisione del dispositivo;
3) errori la cui esistenza può non essere sospettata, ma la cui entità può spesso essere significativa. Tali errori si verificano più spesso in misurazioni complesse. Un semplice esempio di tale errore è la misurazione della densità di un campione contenente una cavità al suo interno;
4) errori causati dalle caratteristiche dell'oggetto di misura stesso. Ad esempio, quando si misura la conduttività elettrica di un metallo, da quest'ultimo viene prelevato un pezzo di filo. Possono verificarsi errori se è presente qualche difetto nel materiale: una crepa, un ispessimento del filo o una disomogeneità che ne modifica la resistenza.
Gli errori casuali sono errori che cambiano casualmente in segno e grandezza in condizioni identiche di misurazioni ripetute della stessa quantità.
Informazioni correlate.
Nessuna misurazione è esente da errori o, più precisamente, la probabilità di una misurazione senza errori si avvicina allo zero. Il tipo e le cause degli errori sono molto diversi e sono influenzati da molti fattori (fig. 1.2).
Le caratteristiche generali dei fattori d'influenza possono essere sistematizzate da vari punti di vista, ad esempio, in base all'influenza dei fattori elencati (Fig. 1.2).
In base ai risultati della misurazione, gli errori possono essere suddivisi in tre tipologie: sistematici, casuali ed errori.
Errori sistematici a loro volta vengono divisi in gruppi in base alla loro occorrenza e alla natura della loro manifestazione. Possono essere eliminati in vari modi, ad esempio introducendo emendamenti.
riso. 1.2
Errori casuali sono causati da un insieme complesso di fattori di cambiamento, solitamente sconosciuti e difficili da analizzare. La loro influenza sul risultato della misurazione può essere ridotta, ad esempio, mediante misurazioni ripetute con ulteriore elaborazione statistica dei risultati ottenuti utilizzando il metodo della teoria della probabilità.
A manca Questi includono errori grossolani che derivano da improvvisi cambiamenti nelle condizioni sperimentali. Anche questi errori sono di natura casuale e, una volta identificati, devono essere eliminati.
L'accuratezza delle misurazioni è valutata dagli errori di misurazione, che sono suddivisi in base alla natura della loro occorrenza in strumentale e metodologico e in base al metodo di calcolo in assoluto, relativo e ridotto.
Strumentale L'errore è caratterizzato dalla classe di precisione del dispositivo di misurazione, che è riportata nel suo passaporto sotto forma di errori principali e aggiuntivi normalizzati.
Metodico l'errore è dovuto all'imperfezione dei metodi e degli strumenti di misurazione.
Assoluto l'errore è la differenza tra i valori G u misurati e i valori G reali di una quantità, determinati dalla formula:
Δ=ΔG=G u -G
Si noti che la quantità ha la dimensione della quantità misurata.
Parente l'errore si trova dall'uguaglianza
δ=±ΔG/G u ·100%
Dato l'errore viene calcolato utilizzando la formula (classe di precisione del dispositivo di misurazione)
δ=±ΔG/G norma ·100%
dove G norme è il valore di normalizzazione della quantità misurata. È considerato uguale a:
a) il valore finale della scala dello strumento, se la tacca di zero è sul bordo o all'esterno della scala;
b) la somma dei valori finali della scala senza tener conto dei segni, se la tacca di zero si trova all'interno della scala;
c) la lunghezza della scala, se la scala non è uniforme.
La classe di precisione di un dispositivo viene stabilita durante i test ed è un errore standardizzato calcolato utilizzando le formule
γ=±ΔG/G norma ·100%, seΔG m =cost

dove ΔG m è il massimo errore assoluto possibile del dispositivo;
G k – valore finale del limite di misurazione del dispositivo; c e d sono coefficienti che tengono conto dei parametri di progettazione e delle proprietà del meccanismo di misurazione del dispositivo.
Ad esempio, per un voltmetro con errore relativo costante, l'uguaglianza vale
δm =±c
Gli errori relativi e ridotti sono legati dalle seguenti dipendenze:
a) per qualsiasi valore dell'errore ridotto
δ=±γ·G norme/G u
b) per l'errore ridotto maggiore
δ=±γ m ·G norme/G u
Da queste relazioni ne consegue che quando si effettuano misurazioni, ad esempio con un voltmetro, in un circuito allo stesso valore di tensione, minore è la tensione misurata, maggiore è l'errore relativo. E se questo voltmetro viene scelto in modo errato, l'errore relativo può essere commisurato al valore Sol n , il che è inaccettabile. Si noti che in conformità con la terminologia dei problemi da risolvere, ad esempio, quando si misura la tensione G = U, quando si misura la corrente C = I, le designazioni delle lettere nelle formule per il calcolo degli errori devono essere sostituite con i simboli corrispondenti.
Esempio 1.1. Un voltmetro con valori γ m = 1,0%, U n = norme G, G k = 450 V, misurare la tensione U u pari a 10 V. Stimiamo gli errori di misura.
Soluzione.

Risposta. L'errore di misurazione è del 45%. Con un tale errore, la tensione misurata non può essere considerata affidabile.
Se le possibilità di scelta di un dispositivo (voltmetro) sono limitate, l'errore metodologico può essere preso in considerazione mediante una modifica calcolata utilizzando la formula

Esempio 1.2. Calcolare l'errore assoluto del voltmetro V7-26 quando si misura la tensione in un circuito CC. La classe di precisione del voltmetro è specificata dall'errore massimo ridotto γ m =±2,5%. Il limite della scala del voltmetro utilizzato nel lavoro è U norma = 30 V.
Soluzione. L'errore assoluto si calcola utilizzando le formule note:
![]()
(poiché l'errore ridotto, per definizione, è espresso dalla formula ![]() , quindi da qui puoi trovare l'errore assoluto:
, quindi da qui puoi trovare l'errore assoluto: ![]()
Risposta.∆U = ±0,75 V.
Passi importanti nel processo di misurazione sono l'elaborazione dei risultati e le regole di arrotondamento. La teoria dei calcoli approssimativi consente, conoscendo il grado di accuratezza dei dati, di valutare il grado di accuratezza dei risultati anche prima di eseguire azioni: selezionare i dati con il grado di accuratezza appropriato, sufficiente a garantire l'accuratezza richiesta del risultato, ma non troppo grande per salvare la calcolatrice da calcoli inutili; razionalizzare il processo di calcolo stesso, liberandolo da quei calcoli che non influenzeranno i numeri e i risultati esatti.
Durante l'elaborazione dei risultati vengono applicate le regole di arrotondamento.
- Regola 1. Se la prima cifra scartata è maggiore di cinque, l'ultima cifra mantenuta viene aumentata di uno.
- Regola 2. Se la prima cifra scartata è inferiore a cinque non viene effettuato alcun incremento.
- Regola 3. Se la cifra scartata è cinque e dietro non ci sono cifre significative, l'arrotondamento viene effettuato al numero pari più vicino, ad es. l'ultima cifra memorizzata rimane la stessa se è pari e aumenta se non è pari.
Se dietro il numero cinque sono presenti cifre significative, l'arrotondamento viene effettuato secondo la regola 2.
Applicando la regola 3 all'arrotondamento di un singolo numero, non aumentiamo la precisione dell'arrotondamento. Ma con molti arrotondamenti, ci saranno numeri in eccesso tanto spesso quanto numeri in difetto. La compensazione reciproca degli errori garantirà la massima precisione del risultato.
Viene chiamato un numero che ovviamente supera l'errore assoluto (o nel peggiore dei casi è uguale ad esso). massimo errore assoluto.
L’entità dell’errore massimo non è del tutto certa. Per ogni numero approssimato è necessario conoscere il suo errore massimo (assoluto o relativo).
Quando non è indicato direttamente, si intende che l'errore massimo assoluto è mezza unità dell'ultima cifra scritta. Pertanto, se viene fornito un numero approssimativo di 4,78 senza indicare l'errore massimo, si presuppone che l'errore assoluto massimo sia 0,005. Come risultato di questo accordo, puoi sempre fare a meno di indicare l'errore massimo di un numero arrotondato secondo le regole 1-3, cioè se il numero approssimativo è indicato con la lettera α, allora
Dove Δn è l'errore massimo assoluto; e δ n è l'errore relativo massimo.
Inoltre, durante l'elaborazione dei risultati, utilizziamo regole per trovare un errore somma, differenza, prodotto e quoziente.
- Regola 1. L'errore massimo assoluto della somma è pari alla somma dei massimi errori assoluti dei singoli termini, ma con un numero significativo di errori dei termini si verifica solitamente una reciproca compensazione degli errori, quindi il vero errore della somma solo in casi eccezionali casi coincide con l’errore massimo o si avvicina ad esso.
- Regola 2. L'errore assoluto massimo della differenza è pari alla somma degli errori assoluti massimi di quello che viene ridotto o sottratto.
L'errore relativo massimo può essere facilmente trovato calcolando l'errore massimo assoluto.
- Regola 3. L'errore relativo massimo della somma (ma non della differenza) si trova tra il più piccolo e il più grande degli errori relativi dei termini.
Se tutti i termini hanno lo stesso errore relativo massimo, allora la somma ha lo stesso errore relativo massimo. In altre parole, in questo caso l'accuratezza della somma (in termini percentuali) non è inferiore all'accuratezza dei termini.
A differenza della somma, la differenza dei numeri approssimati può essere meno precisa del minuendo e del sottraendo. La perdita di precisione è particolarmente grande quando minuendo e sottraendo differiscono poco tra loro.
- Regola 4. L'errore relativo massimo del prodotto è approssimativamente pari alla somma degli errori relativi massimi dei fattori: δ=δ 1 +δ 2, o più precisamente δ=δ 1 +δ 2 +δ 1 δ 2 dove δ è l'errore relativo del prodotto, δ 1 δ 2 - fattori di errori relativi.
Appunti:
1. Se si moltiplicano numeri approssimativi con lo stesso numero di cifre significative, lo stesso numero di cifre significative deve essere mantenuto nel prodotto. L'ultima cifra memorizzata non sarà completamente affidabile.
2. Se alcuni fattori hanno cifre più significative di altri, allora prima di moltiplicare, i primi dovrebbero essere arrotondati, mantenendo in essi tante cifre quanto il fattore meno accurato o uno in più (come riserva), salvare ulteriori cifre è inutile.
3. Se è richiesto che il prodotto di due numeri abbia un numero predeterminato che sia completamente affidabile, allora in ciascuno dei fattori il numero di cifre esatte (ottenute mediante misurazione o calcolo) deve essere uno in più. Se il numero di fattori è superiore a due e inferiore a dieci, in ciascuno dei fattori il numero di cifre esatte per una garanzia completa deve essere due unità in più rispetto al numero di cifre esatte richiesto. In pratica è sufficiente prendere solo una cifra in più.
- Regola 5. L'errore relativo massimo del quoziente è approssimativamente uguale alla somma degli errori relativi massimi del dividendo e del divisore. Il valore esatto dell'errore relativo massimo supera sempre quello approssimato. La percentuale di eccesso è approssimativamente uguale all'errore relativo massimo del divisore.
Esempio 1.3. Trova l'errore assoluto massimo del quoziente 2,81: 0,571.
Soluzione. L'errore relativo massimo del dividendo è 0,005:2,81=0,2%; divisore – 0,005:0,571=0,1%; privato – 0,2% + 0,1% = 0,3%. L'errore assoluto massimo del quoziente sarà circa 2,81: 0,571·0,0030=0,015
Ciò significa che nel quoziente 2,81:0,571=4,92 la terza cifra significativa non è attendibile.
Risposta. 0,015.
Esempio 1.4. Calcola l'errore relativo delle letture di un voltmetro collegato secondo il circuito (Fig. 1.3), che si ottiene se assumiamo che il voltmetro abbia una resistenza infinitamente grande e non introduca distorsioni nel circuito misurato. Classificare l'errore di misurazione per questo problema.

riso. 1.3
Soluzione. Indichiamo le letture di un voltmetro reale con AND e un voltmetro con resistenza infinitamente alta con AND ∞. Errore relativo richiesto ![]()
notare che
allora otteniamo
Poiché R AND >>R e R > r, la frazione al denominatore dell'ultima uguaglianza è molto inferiore a uno. Pertanto, è possibile utilizzare la formula approssimativa ![]() , valido per λ≤1 per qualsiasi α. Supponendo che in questa formula α = -1 e λ= rR (r+R) -1 R And -1, otteniamo δ ≈ rR/(r+R) R And.
, valido per λ≤1 per qualsiasi α. Supponendo che in questa formula α = -1 e λ= rR (r+R) -1 R And -1, otteniamo δ ≈ rR/(r+R) R And.
Maggiore è la resistenza del voltmetro rispetto alla resistenza esterna del circuito, minore è l'errore. Ma la condizione R< Risposta. Errore metodologico sistematico. Esempio 1.5.
Il circuito DC (Fig. 1.4) comprende i seguenti dispositivi: A – amperometro tipo M 330, classe di precisione K A = 1,5 con limite di misurazione I k = 20 A; A 1 - amperometro tipo M 366, classe di precisione K A1 = 1,0 con un limite di misurazione I k1 = 7,5 A. Trova il massimo errore relativo possibile nella misurazione della corrente I 2 e i possibili limiti del suo valore effettivo, se gli strumenti lo hanno mostrato I = 8,0A. e I1 = 6,0A. Classificare la misurazione. riso. 1.4 Soluzione. Determiniamo la corrente I 2 dalle letture del dispositivo (senza tener conto dei loro errori): I 2 =I-I 1 =8,0-6,0=2,0 A. Troviamo i moduli di errore assoluto degli amperometri A e A 1 Per A abbiamo l'uguaglianza Troviamo la somma dei moduli di errore assoluto: Di conseguenza, il valore più grande possibile dello stesso valore, espresso in frazioni di questo valore, è pari a 1. 10 3 – per un dispositivo; 2·10 3 – per un altro dispositivo. Quale di questi dispositivi sarà il più preciso? Soluzione. La precisione del dispositivo è caratterizzata dal reciproco dell'errore (più preciso è il dispositivo, minore è l'errore), cioè per il primo dispositivo questo sarà 1/(1 . 10 3) = 1000, per il secondo – 1/(2 . 10 3) = 500. Si noti che 1000 > 500. Pertanto, il primo dispositivo è due volte più accurato del il secondo. Una conclusione simile può essere raggiunta verificando la coerenza degli errori: 2. 10 3/1. 103 = 2. Risposta. Il primo dispositivo è due volte più preciso del secondo. Esempio 1.6.
Trova la somma delle misure approssimative del dispositivo. Trova il numero di caratteri corretti: 0,0909 + 0,0833 + 0,0769 + 0,0714 + 0,0667 + 0,0625 + 0,0588+ 0,0556 + 0,0526. Soluzione. Sommando tutti i risultati delle misurazioni, otteniamo 0,6187. L'errore massimo massimo della somma è 0,00005·9=0,00045. Ciò significa che nell'ultima quarta cifra della somma è possibile un errore fino a 5 unità. Pertanto, arrotondiamo l'importo alla terza cifra, ad es. millesimi, otteniamo 0,619, un risultato in cui tutti i segni sono corretti. Risposta. 0,619. Il numero di cifre corrette è di tre cifre decimali. Il problema è formulato come segue: lasciamo la quantità desiderata z determinato attraverso altre quantità a, b, c, ... ottenuti da misurazioni dirette z = f (a, b, c,...) (1.11) È necessario trovare il valore medio della funzione e l'errore delle sue misurazioni, ad es. trovare l'intervallo di confidenza con affidabilità a e relativo errore. Per quanto riguarda, si trova sostituendo nella parte destra di (11) invece di a, b, c,...i loro valori medi 3. Stimare la semiampiezza dell'intervallo di confidenza per il risultato delle misurazioni indirette dove i derivati... vengono calcolati 4. Determinare l'errore relativo del risultato 5. Se la dipendenza di z da a, b, c,... ha la forma poi assoluto . 6. Scrivi il risultato finale nel modulo z = ± Dz , ε = …% in a =
… . Nota: Quando si elaborano i risultati delle misurazioni dirette, è necessario seguire la seguente regola: i valori numerici di tutte le quantità calcolate devono contenere una cifra in più rispetto alle quantità originali (determinate sperimentalmente). Per le misurazioni indirette, i calcoli vengono effettuati secondo regole di calcolo approssimativo: Regola 1.
Quando aggiungi e sottrai numeri approssimativi, devi: a) selezionare il termine in cui la cifra dubbia ha la cifra più alta; b) arrotondare tutti gli altri termini alla cifra successiva (viene mantenuta una cifra di riserva); c) eseguire addizioni (sottrazioni); d) scartare di conseguenza l'ultima cifra mediante arrotondamento (la cifra della cifra dubbia del risultato coincide con la più alta delle cifre delle cifre dubbie dei termini). Esempio: 5.4382·10 5 – 2.918·10 3 + 35,8 + 0,064. In questi numeri le ultime cifre significative sono dubbie (quelle errate sono già state scartate). Scriviamoli nella forma 543820 – 2918 + 35,8 + 0,064. Si può vedere che nel primo termine il numero dubbio 2 ha la cifra più alta (le decine). Arrotondando tutti gli altri numeri alla cifra successiva e sommando, otteniamo 543820 – 2918 + 36 + 0 = 540940 = 5,4094 10 5. Regola 2.
Quando moltiplichi (dividi) numeri approssimati devi: a) selezionare il/i numero/i con il minor numero di cifre significative ( SIGNIFICATIVO – numeri diversi dallo zero e zeri tra di loro); b) arrotondare i numeri rimanenti in modo che abbiano una cifra significativa in più (viene mantenuta una cifra di riserva) rispetto a quelle assegnate al passaggio a; c) moltiplicare (dividere) i numeri risultanti; d) lasciare di conseguenza tante cifre significative quante erano nel/i numero/i con meno cifre significative. Esempio: . Regola 3.
Quando elevato a una potenza, quando si estrae una radice, il risultato conserva tante cifre significative quante sono nel numero originale. Esempio: Regola 4.
Quando si trova il logaritmo di un numero, la mantissa del logaritmo deve avere tante cifre significative quante sono il numero originale: Esempio: Nella registrazione finale assoluto gli errori dovrebbero essere lasciati solo una cifra significativa. (Se questa cifra risulta essere 1, dopo di essa viene memorizzata un'altra cifra). Il valore medio viene arrotondato alla stessa cifra dell'errore assoluto. Per esempio: V= (375,21 0,03) cm 3 = (3,7521 0,0003) cm 3. IO= (5,530 0,013) A, UN = Ordine di lavoro
Determinazione del diametro del cilindro.
1. Utilizzando un calibro, misurare il diametro del cilindro 7 volte (in diversi punti e direzioni). Registra i risultati in una tabella. Informazioni correlate: Errori nelle quantità misurate e tabulate determinano gli errori di DH avg del valore determinato indirettamente e il contributo maggiore a DH avg è dato dai valori meno accurati, che hanno l'errore relativo massimo D. Pertanto, per aumentare la precisione delle misurazioni indirette, è necessario raggiungere la stessa precisione delle misurazioni dirette (d A, d B, d C, ...). Regole per trovare errori nelle misurazioni indirette: 1. Trova il logaritmo naturale della funzione data ln(X = f(A,B,C,…)); 2. Trova il differenziale totale (su tutte le variabili) dal logaritmo naturale trovato della funzione data; 3. Sostituire il segno del differenziale d con il segno dell'errore assoluto D; 4. Sostituisci tutti gli "svantaggi" che comportano errori assoluti DA, DB, DC, ... ai "professionisti". Il risultato è la formula per l'errore relativo più grande dx valore misurato indirettamente X: dx = = j (A medio, B medio, C medio, ..., DA medio, DB medio, DC medio, ...).(18) Secondo l'errore relativo trovato dx determinare l'errore assoluto della misurazione indiretta: DX av = dx. X media . (19) Il risultato delle misurazioni indirette è scritto in forma standard e rappresentato sull'asse numerico: X = (X medio ± DХ medio), unità. (20) Esempio:
Trova i valori degli errori relativi e medi di una quantità fisica l, determinato indirettamente dalla formula: Dove π, g, t, k, α, β– grandezze i cui valori sono misurati o presi da tabelle di riferimento e inseriti in una tabella di risultati di misurazione e dati tabulati (simile alla Tabella 1). 1. Calcolare il valore medio Lav, sostituendo i valori medi della tabella nella (21) – π medio, g medio, t medio, k medio, α medio, β medio. 2. Determinare l'errore relativo più grande δL: UN). Formula del logaritmo (21): B). L'espressione risultante (22) è differenziata: c) Sostituisci il segno del differenziale d con Δ e i "meno" davanti agli errori assoluti con "più" e ottieni un'espressione per l'errore relativo più grande. δL: D). Sostituendo i valori medi delle quantità di input e i loro errori dalla tabella dei risultati di misurazione nell'espressione risultante, calcola δL. 3. Quindi calcolare l'errore assoluto ΔL medio: Il risultato viene registrato in forma standard e rappresentato graficamente sull'asse l: STIME ELEMENTARI DELL'ERRORE DI MISURA La misurazione consiste nel trovare sperimentalmente il valore di una quantità fisica con l'aiuto di mezzi tecnici speciali: misure, strumenti di misurazione. Una misura è un mezzo di misura che riproduce una quantità fisica di una determinata dimensione: un'unità di misura, il suo valore multiplo o frazionario. Ad esempio, pesa 1 kg, 5 kg, 10 kg. Un dispositivo di misurazione è uno strumento di misurazione progettato per generare un segnale di misurazione delle informazioni in una forma accessibile alla percezione diretta da parte di un osservatore. Un dispositivo di misurazione consente di confrontare direttamente o indirettamente il valore misurato con le misure. Anche le misurazioni si dividono in dirette e indirette. Nelle misurazioni dirette, il valore desiderato della quantità si trova direttamente dai dati di base (sperimentali). Nelle misurazioni indirette, il valore desiderato di una grandezza si trova in base alla relazione nota tra tale grandezza e le grandezze sottoposte a misurazioni dirette. Il principio di misurazione è un insieme di fenomeni fisici su cui si basano le misurazioni. Un metodo di misurazione è un insieme di tecniche per utilizzare principi e strumenti di misura. Il valore di una grandezza fisica, che idealmente rifletterebbe in termini qualitativi e quantitativi la corrispondente proprietà di un dato oggetto, è il vero valore della grandezza fisica. Il valore di una grandezza fisica trovato misurandola è il risultato della misurazione. La deviazione del risultato della misurazione dal valore reale del valore misurato è l'errore di misurazione. L'errore di misurazione assoluto è l'errore di misurazione, espresso in unità del valore misurato e pari alla differenza tra il risultato e il valore reale del valore misurato. Il rapporto tra l'errore assoluto e il valore reale della quantità misurata è l'errore relativo di misurazione. I contributi all'errore di misurazione includono errori negli strumenti di misurazione (errore strumentale o strumentale), imperfezione del metodo di misurazione, errore nella lettura sulla scala dello strumento, influenze esterne sui mezzi e sugli oggetti di misurazione e ritardo nella reazione umana ai segnali luminosi e sonori . In base alla natura della loro manifestazione, gli errori si dividono in sistematici e casuali. Un evento casuale è un evento che, dato un dato insieme di fattori, può verificarsi o meno. L'errore casuale è una componente dell'errore di misurazione che cambia in modo casuale con misurazioni ripetute della stessa quantità. Una caratteristica degli errori casuali è un cambiamento nell'entità e nel segno dell'errore in condizioni di misurazione costanti. L'errore sistematico è una componente dell'errore di misurazione che rimane costante o cambia naturalmente con misurazioni ripetute della stessa quantità. Gli errori sistematici, in linea di principio, possono essere eliminati attraverso correzioni e l’uso di strumenti e metodi più accurati (anche se nella pratica non è sempre facile individuare errori sistematici). È impossibile escludere errori casuali nelle singole misurazioni; la teoria matematica dei fenomeni casuali (teoria della probabilità) consente solo di stabilire una stima ragionevole della loro entità. Supponiamo che gli errori sistematici siano esclusi e che gli errori nei risultati della misurazione siano solo casuali. Indichiamo con lettere i risultati delle misurazioni di una quantità fisica, il cui vero valore è uguale a Sommando i lati sinistro e destro dell'uguaglianza (1), otteniamo: La teoria degli errori casuali si basa su ipotesi confermate dall’esperienza: gli errori possono assumere una serie continua di valori; con un gran numero di misurazioni, errori casuali della stessa entità, ma di segno diverso, si verificano altrettanto spesso; la probabilità di un errore diminuisce all’aumentare della sua entità. È inoltre necessario che gli errori siano piccoli rispetto al valore misurato e indipendenti. Secondo l'ipotesi (1), con il numero di misurazioni n otteniamo Tuttavia, il numero di dimensioni è sempre finito e Secondo la teoria della probabilità, la media aritmetica di una serie di misurazioni La probabilità che il valore desiderato (il suo vero valore) sia contenuto nell'intervallo (a - a, a + a) sarà chiamata probabilità di confidenza (affidabilità) , e il corrispondente intervallo (a - a, a + a) - intervallo di confidenza; Quanto più piccolo è l'errore a, tanto minore è la probabilità che il valore misurato sia contenuto nell'intervallo definito da questo errore. È vera anche l'affermazione opposta: meno affidabile è il risultato, più stretto è l'intervallo di confidenza del valore desiderato. Per n grande (praticamente per n 100), la semiampiezza dell'intervallo di confidenza per una data affidabilità è uguale a dove K() = 1 in = 0,68; K() = 2 in = 0,95; K() = 3 in = 0,997. Con un numero limitato di misurazioni, che si riscontra più spesso nella pratica di laboratorio degli studenti, il coefficiente K() in (3) dipende non solo da , ma anche dal numero di misurazioni n. Pertanto, in presenza del solo errore casuale, troveremo sempre la semiampiezza dell'intervallo di confidenza utilizzando la formula Nella (4), il coefficiente t n è chiamato coefficiente di Student. Per = 0,95 adottato nel lavoro pratico degli studenti, i valori di t n sono i seguenti: Il valore è chiamato errore quadratico medio della media aritmetica di una serie di misurazioni. L'errore di uno strumento o di una misura è solitamente indicato sul suo passaporto o da un simbolo sulla scala dello strumento. Solitamente per errore strumentale si intende la semiampiezza dell'intervallo entro il quale può essere contenuto il valore misurato con una probabilità di misura pari a 0,997, se l'errore di misura è dovuto solo all'errore strumentale. Come errore generale (totale) del risultato della misurazione, accetteremo con probabilità = 0,95 L'errore assoluto consente di determinare in quale segno del risultato ottenuto è contenuta l'imprecisione. L'errore relativo fornisce informazioni su quale proporzione (percentuale) del valore misurato è l'errore (metà ampiezza dell'intervallo di confidenza). Scriviamo il risultato finale di una serie di misurazioni dirette del valore a 0 nel modulo Per esempio Pertanto, qualsiasi grandezza fisica trovata sperimentalmente deve essere rappresentata: Le dimensioni sono chiamate Dritto, se i valori delle quantità sono determinati direttamente da strumenti (ad esempio, misurare la lunghezza con un righello, determinare il tempo con un cronometro, ecc.). Le dimensioni sono chiamate indiretto, se il valore della grandezza misurata è determinato attraverso misurazioni dirette di altre grandezze associate alla specifica relazione da misurare. Errore assoluto e relativo. Lasciamo che venga eseguito N misurazioni della stessa quantità X in assenza di errore sistematico. I risultati delle misurazioni individuali sono i seguenti: X 1
,X 2
,
…,X N. Il valore medio del valore misurato viene selezionato come il migliore: Errore assoluto di una singola misura è chiamata differenza della forma: Errore assoluto medio N misure unitarie: chiamato errore medio assoluto. Errore relativo Il rapporto tra l'errore medio assoluto e il valore medio della grandezza misurata è chiamato: Se non ci sono istruzioni speciali, l'errore dello strumento è pari alla metà del suo valore di divisione (righello, bicchiere). L'errore degli strumenti dotati di nonio è uguale al valore della divisione del nonio (micrometro - 0,01 mm, calibro - 0,1 mm). L'errore dei valori della tabella è pari a mezza unità dell'ultima cifra (cinque unità dell'ordine successivo all'ultima cifra significativa). L'errore degli strumenti di misura elettrici viene calcolato in base alla classe di precisione CON indicato sulla scala dello strumento: Per esempio: Dove U massimo E IO massimo– limite di misura del dispositivo. L'errore dei dispositivi con display digitale è pari ad una delle ultime cifre del display. Dopo aver valutato gli errori casuali e strumentali, si tiene conto di quello il cui valore è maggiore. La maggior parte delle misurazioni sono indirette. In questo caso il valore desiderato X è funzione di più variabili UN,B,
C…
, i cui valori possono essere trovati mediante misurazioni dirette: X = f( UN,
B,
C…). La media aritmetica del risultato delle misurazioni indirette sarà pari a: X = f( UN, B, C…). Un modo per calcolare l'errore è differenziare il logaritmo naturale della funzione X = f( UN,
B,
C...). Se, ad esempio, il valore desiderato X è determinato dalla relazione X = Il differenziale di questa espressione ha la forma: In relazione al calcolo dei valori approssimativi, si può scrivere per il relativo errore nella forma: =
L'errore assoluto si calcola utilizzando la formula: Х = Х(5) Pertanto, il calcolo degli errori e il calcolo del risultato per le misurazioni indirette vengono eseguiti nel seguente ordine: 1) Misurare tutte le quantità incluse nella formula iniziale per calcolare il risultato finale. 2) Calcolare i valori medi aritmetici di ciascun valore misurato e i relativi errori assoluti. 3) Sostituire i valori medi di tutti i valori misurati nella formula originale e calcolare il valore medio del valore desiderato: X = f( UN, B, C…). 4) Logaritmo della formula originale X = f( UN,
B,
C...) e trascrivere l'espressione del relativo errore sotto forma di formula (4). 5) Calcolare l'errore relativo = 6) Calcolare l'errore assoluto del risultato utilizzando la formula (5). 7) Il risultato finale si scrive come: X = X media X Gli errori assoluti e relativi delle funzioni più semplici sono riportati nella tabella: Assoluto errore Parente errore a+
B a+
B Errori sistematici. Errori sistematici modificano naturalmente i valori della quantità misurata. Gli errori introdotti nelle misurazioni dagli strumenti sono valutabili più facilmente se sono associati alle caratteristiche progettuali degli strumenti stessi. Questi errori sono indicati nei passaporti dei dispositivi. Gli errori di alcuni dispositivi possono essere valutati senza fare riferimento alla scheda tecnica. Per molti strumenti di misura elettrici la classe di precisione è indicata direttamente sulla scala. Classe di precisione dello strumento- questo è il rapporto tra l'errore assoluto del dispositivo e il valore massimo della quantità misurata, che può essere determinato utilizzando questo dispositivo (questo è l'errore relativo sistematico di questo dispositivo, espresso come percentuale del valore della scala). Quindi l'errore assoluto di tale dispositivo è determinato dalla relazione: Per gli strumenti di misura elettrici sono state introdotte 8 classi di precisione: 0,05; 0,1; 0,5; 1,0; 1,5; 2.0; 2,5; 4. Più il valore misurato si avvicina al valore nominale, più accurato sarà il risultato della misurazione. La massima precisione (ovvero il più piccolo errore relativo) che un dato dispositivo può fornire è pari alla classe di precisione. Questa circostanza deve essere presa in considerazione quando si utilizzano strumenti multiscala. La scala deve essere scelta in modo tale che il valore misurato, pur rimanendo all'interno della scala, si avvicini il più possibile al valore nominale. Se la classe di precisione del dispositivo non è specificata, è necessario seguire le seguenti regole: · L'errore assoluto degli strumenti dotati di nonio è pari alla precisione del nonio. · L'errore assoluto degli strumenti con passo della freccia fisso è pari al valore della divisione. · L'errore assoluto dei dispositivi digitali è pari ad una cifra minima. · Per tutti gli altri strumenti si assume che l'errore assoluto sia pari alla metà del valore della divisione. Errori casuali. Questi errori sono di natura statistica e sono descritti dalla teoria della probabilità. È stato stabilito che con un numero molto elevato di misurazioni, la probabilità di ottenere l'uno o l'altro risultato in ogni singola misurazione può essere determinata utilizzando la distribuzione normale gaussiana. Con un numero limitato di misurazioni, la descrizione matematica della probabilità di ottenere l'uno o l'altro risultato della misurazione è chiamata distribuzione di Student (puoi leggere ulteriori informazioni al riguardo nel manuale di I.L. Skvortsova "Errori di misurazione nelle quantità fisiche"). Come valutare il valore reale della quantità misurata? Supponiamo che misurando un certo valore abbiamo ricevuto N risultati: 1). Calcolato media serie di N misure dirette: 2). Calcolato errore casuale assoluto di ciascuna misurazioneè la differenza tra la media aritmetica di una serie di N misurazioni dirette e questa misurazione: 3). Calcolato errore quadratico medio assoluto: 4). Calcolato errore casuale assoluto. Con un piccolo numero di misurazioni, l'errore casuale assoluto può essere calcolato attraverso l'errore quadratico medio e un certo coefficiente chiamato coefficiente di Student: Il coefficiente di Student dipende dal numero di misurazioni N e dal coefficiente di affidabilità (la Tabella 1 mostra la dipendenza del coefficiente di Student dal numero di misurazioni a un valore fisso del coefficiente di affidabilità). Fattore di affidabilitàè la probabilità con cui il valore vero del valore misurato rientra nell'intervallo di confidenza. Intervallo di confidenza Pertanto, il coefficiente di Student è il numero per il quale deve essere moltiplicato l'errore quadratico medio per garantire l'affidabilità specificata del risultato per un dato numero di misurazioni. Maggiore è l'affidabilità richiesta per un dato numero di misurazioni, maggiore è il coefficiente di Student. D'altra parte, maggiore è il numero di misurazioni, minore è il coefficiente di Student per una data affidabilità. Nel lavoro di laboratorio della nostra officina, assumeremo che l'affidabilità sia data e pari a 0,9. I valori numerici dei coefficienti di Student per questa affidabilità per diversi numeri di misurazioni sono riportati nella Tabella 1. Tabella 1 5).Calcolato errore assoluto totale. In ogni misurazione ci sono errori sia casuali che sistematici. Calcolare l'errore di misurazione assoluto totale (totale) non è un compito facile, poiché questi errori sono di natura diversa. Per le misurazioni ingegneristiche, ha senso sommare gli errori assoluti sistematici e casuali Per semplicità di calcolo, è consuetudine stimare l'errore assoluto totale come la somma degli errori casuali assoluti e sistematici (strumentali) assoluti, se gli errori sono dello stesso ordine di grandezza, e trascurare uno degli errori se è più di un ordine di grandezza (10 volte) più piccolo dell'altro. 6). L'errore e il risultato vengono arrotondati. Poiché il risultato della misurazione viene presentato come un intervallo di valori, il cui valore è determinato dall'errore assoluto totale, è importante il corretto arrotondamento del risultato e dell'errore. L'arrotondamento inizia con errore assoluto!!! Il numero di cifre significative che rimangono nel valore dell'errore, in generale, dipende dal coefficiente di affidabilità e dal numero di misurazioni. Tuttavia, anche per misurazioni molto precise (ad esempio astronomiche), in cui è importante il valore esatto dell'errore, non lasciare più di due cifre significative. Un numero maggiore di numeri non ha senso, poiché la stessa definizione di errore ha il proprio errore. La nostra pratica ha un coefficiente di affidabilità relativamente piccolo e un numero limitato di misurazioni. Pertanto, quando si arrotonda (con eccesso), l'errore assoluto totale viene lasciato a una cifra significativa. La cifra significativa dell'errore assoluto determina la cifra della prima cifra dubbia nel valore del risultato. Di conseguenza, il valore del risultato stesso deve essere arrotondato (con correzione) a quella cifra significativa la cui cifra coincide con la cifra significativa dell'errore. La regola formulata dovrebbe essere applicata anche nei casi in cui alcuni numeri sono zeri. Se il risultato ottenuto misurando il peso corporeo è 0,900, è necessario scrivere degli zeri alla fine del numero. La registrazione significherebbe che non si sapeva nulla delle successive cifre significative, mentre le misurazioni mostravano che erano pari a zero. 7). Calcolato errore relativo . Nell'arrotondamento dell'errore relativo è sufficiente lasciare due cifre significative. il risultato di una serie di misurazioni di una determinata quantità fisica è presentato sotto forma di un intervallo di valori, indicando la probabilità che il valore vero rientri in questo intervallo, ovvero il risultato deve essere scritto nella forma: Ecco l'errore assoluto totale, arrotondato alla prima cifra significativa, ed è il valore medio del valore misurato, arrotondato tenendo conto dell'errore già arrotondato. Quando si registra un risultato di misurazione è necessario indicare l'unità di misura del valore. Diamo un'occhiata ad alcuni esempi: 1. Supponiamo che misurando la lunghezza di un segmento, abbiamo ricevuto il seguente risultato: cm e cm Come annotare correttamente il risultato della misurazione della lunghezza di un segmento? Per prima cosa arrotondiamo l'errore assoluto con l'eccesso, lasciando una cifra significativa, vedi. Quindi arrotondiamo il valore medio corretto al centesimo più vicino, cioè alla cifra significativa la cui cifra coincide con la cifra significativa dell'errore 
![]() per amperometro
per amperometro ![]()
 ,
,![]()
![]() , Dove k, l, m‒ qualsiasi numero reale, devi prima trovarlo parente errore
, Dove k, l, m‒ qualsiasi numero reale, devi prima trovarlo parente errore
![]() .
.![]() .
.![]() J.
J.NO. d io, mm
d io-
(d io-
) 2
ciao io, mm E

 , (21)
, (21)![]()
![]() , unità modifica
, unità modificaErrori di misurazioni dirette
![]() . Sono indicati gli errori assoluti dei risultati delle singole misurazioni:
. Sono indicati gli errori assoluti dei risultati delle singole misurazioni: (2)
(2)
 ,
,![]() rimane sconosciuto. Ma ai fini pratici è sufficiente trovare sperimentalmente il valore di una grandezza fisica così vicina a quella vera che
rimane sconosciuto. Ma ai fini pratici è sufficiente trovare sperimentalmente il valore di una grandezza fisica così vicina a quella vera che  può essere utilizzato invece di true. La domanda è: come valutare il grado di questa approssimazione?
può essere utilizzato invece di true. La domanda è: come valutare il grado di questa approssimazione? più affidabile dei risultati delle singole misurazioni, perché sono ugualmente probabili deviazioni casuali dal valore reale in direzioni diverse. La probabilità della comparsa di un valore ai in un intervallo di larghezza 2a i è intesa come la frequenza relativa di occorrenza dei valori di a i che rientrano nell'intervallo 2a i rispetto al numero di tutti i valori che compaiono di a i con il numero di esperimenti (misure) tendente all'infinito. Ovviamente la probabilità di un evento affidabile è pari a uno, la probabilità di un evento impossibile è pari a zero, cioè 0 100%.
più affidabile dei risultati delle singole misurazioni, perché sono ugualmente probabili deviazioni casuali dal valore reale in direzioni diverse. La probabilità della comparsa di un valore ai in un intervallo di larghezza 2a i è intesa come la frequenza relativa di occorrenza dei valori di a i che rientrano nell'intervallo 2a i rispetto al numero di tutti i valori che compaiono di a i con il numero di esperimenti (misure) tendente all'infinito. Ovviamente la probabilità di un evento affidabile è pari a uno, la probabilità di un evento impossibile è pari a zero, cioè 0 100%. ,
(3)
,
(3) (4)
(4)
 .
. (6)
(6)
Errori casuali nelle misurazioni dirette
 .
. (2)
(2) .
(3)
.
(3)Errori strumentali nelle misure dirette
 E
E  ,
,Calcolo degli errori nelle misure indirette
 , quindi dopo il logaritmo otteniamo: lnX = ln UN+ln B+ln( C+
D).
, quindi dopo il logaritmo otteniamo: lnX = ln UN+ln B+ln( C+
D). .
. .
(4)
.
(4) .
.


![]() .
.![]() . La media aritmetica di una serie di misurazioni è più vicina al valore reale della quantità misurata rispetto alla maggior parte delle misurazioni individuali. Per ottenere il risultato della misurazione di un determinato valore, viene utilizzato il seguente algoritmo.
. La media aritmetica di una serie di misurazioni è più vicina al valore reale della quantità misurata rispetto alla maggior parte delle misurazioni individuali. Per ottenere il risultato della misurazione di un determinato valore, viene utilizzato il seguente algoritmo.![]() .
. .
.![]() ,
,![]() è un intervallo numerico nel quale rientra con una certa probabilità il vero valore della grandezza misurata.
è un intervallo numerico nel quale rientra con una certa probabilità il vero valore della grandezza misurata.![]() .
.![]() vedere Calcolare l'errore relativo
vedere Calcolare l'errore relativo