בעזרת שיעור וידאו זה, כל אחד יוכל להכיר באופן עצמאי את הנושא "הרעיון של פולידרון. פּרִיזמָה. שטח פנים של מנסרה ". במהלך השיעור, המורה ידבר על מהן צורות גיאומטריות כמו פולידרונים ומנסרות, ייתן הגדרות מתאימות ויסביר את מהותן בעזרת דוגמאות ספציפיות.

בעזרת שיעור זה, כל אחד יוכל להכיר באופן עצמאי את הנושא "הקונספט של פולידרון. פּרִיזמָה. שטח פנים של מנסרה ".

הַגדָרָה... משטח המורכב מצולעים ותוחם גוף כלשהו גיאומטרי ייקרא משטח רב קדיר או פולידרון.

שקול את הדוגמאות הבאות של פולידרה:

1. טטרהדרון א ב ג דהוא משטח המורכב מארבעה משולשים: א ב ג, ADB, BDCו ADC(איור 1).

אורז. אחד

2. במקביל ABCDA 1 B 1 C 1 D 1הוא משטח המורכב משישה מקביליות (איור 2).

אורז. 2

המרכיבים העיקריים של פולידרון הם פנים, קצוות וקודקודים.

פנים הם מצולעים המרכיבים פולידרון.

הקצוות הם צדי הפנים.

הקודקודים הם קצות הצלעות.

שקול טטרהדרון א ב ג ד(איור 1). בואו נציין את המרכיבים העיקריים שלה.

פנים: משולשים ABC, ADB, BDC, ADC.

צלעות: AB, AC, BC, DC, מוֹדָעָה, BD.

חולצות: א ב ג ד.

שקול מקבילה ABCDA 1 B 1 C 1 D 1(איור 2).

פנים: מקביליות AA 1 D 1 D, D 1 DСС 1, BB 1 C 1 C, AA 1 B 1 B, ABCD, A 1 B 1 C 1 D 1.

צלעות: AA 1 , BB 1 , SS 1 , DD 1, AD, A 1 D 1, B 1 C 1, BC, AB, A 1 B 1, D 1 C 1, DC.

חולצות: A, B, C, D, A 1, B 1, C 1, D 1.

מקרה מיוחד וחשוב של פולידרון הוא מנסרה.

ABCA 1 B 1 C 1(איור 3).

אורז. 3

משולשים שווים א ב גו A 1 B 1 C 1ממוקמים במישורים מקבילים α ו- β כך שהקצוות AA 1, BB 1, CC 1הם מקבילים.

כְּלוֹמַר ABCA 1 B 1 C 1- מנסרה משולשת אם:

1) משולשים א ב גו A 1 B 1 C 1שווים.

2) משולשים א ב גו A 1 B 1 C 1ממוקמים במישורים מקבילים α ו- β: א ב ג║A 1 B 1 C (α ║ β).

3) צלעות AA 1, BB 1, CC 1הם מקבילים.

א ב גו A 1 B 1 C 1- בסיסי המנסרה.

AA 1, BB 1, CC 1- קצוות רוחביים של המנסרה.

אם מנקודה שרירותית H 1מטוס אחד (למשל, β), הורד את הניצב NN 1במישור α, אז בניצב זה נקרא גובה המנסרה.

הַגדָרָה... אם הקצוות לרוחב בניצב לבסיסים, אז המנסרה נקראת ישרה, אחרת - נוטה.

שקול מנסרה משולשת ABCA 1 B 1 C 1(איור 4). המנסרה הזו היא ישרה. כלומר, הקצוות לרוחבו בניצב לבסיסים.

למשל קצה AA 1בניצב למישור א ב ג... קָצֶה AA 1הוא גובה המנסרה הזו.

אורז. 4

שים לב שהפנים הצדדיות AA 1 B 1 Bבניצב לבסיסים א ב גו A 1 B 1 C 1מכיוון שהוא עובר במאונך AA 1לשטח.

עכשיו שקלו מנסרה אלכסונית ABCA 1 B 1 C 1(איור 5). כאן, הצלע הרוחבית אינה מאונכת למישור הבסיס. אם נשמיט מהנקודה א 1אֲנָכִי A 1 Hעל א ב ג, אז בניצב זה יהיה גובה המנסרה. שימו לב שהקטע ANהיא ההקרנה של הקטע AA 1על המטוס א ב ג.

ואז הזווית בין הקו הישר AA 1ומטוס א ב גזוהי הזווית בין הקו הישר AA 1והיא ANהקרנה על מטוס, כלומר הזווית A 1 AN.

אורז. חָמֵשׁ

שקול מנסרה מרובעת ABCDA 1 B 1 C 1 D 1(איור 6). בואו נראה איך זה יוצא.

1) מרובע א ב ג דשווה לריבוע A 1 B 1 C 1 D 1: ABCD = A 1 B 1 C 1 D 1.

2) מרובעים א ב ג דו A 1 B 1 C 1 D 1 א ב ג║A 1 B 1 C (α ║ β).

3) מרובעים א ב ג דו A 1 B 1 C 1 D 1מסודרים כך שצלעות הצד יהיו מקבילות, כלומר: AA 1 ║В 1 ║СС 1 ║DD 1.

הַגדָרָה... אלכסון מנסרה הוא קטע קו המחבר בין שני קודקודים של פריזמה שאינם שייכים לאותם פנים.

לדוגמה, AC 1- אלכסון של מנסרה מרובעת ABCDA 1 B 1 C 1 D 1.

הַגדָרָה... אם הצלע הצדדית AA 1בניצב למישור הבסיס, אז מנסרה כזו נקראת קו ישר.

אורז. 6

מקרה מסוים של מנסרה מרובעת הוא המקביל האפיפי. מַקבִּילוֹן ABCDA 1 B 1 C 1 D 1מוצג באיור. 7.

בואו נראה איך זה עובד:

1) דמויות שוות מונחות בבסיסים. במקרה זה מקבילות שוות א ב ג דו A 1 B 1 C 1 D 1: א ב ג ד = A 1 B 1 C 1 D 1.

2) מקביליות א ב ג דו A 1 B 1 C 1 D 1שוכבים במישורים מקבילים α ו- β: א ב ג║A 1 B 1 C 1 (α ║ β).

3) מקביליות א ב ג דו A 1 B 1 C 1 D 1מסודרים בצורה כזו שצלעות הצד מקבילות זו לזו: AA 1 ║В 1 ║СС 1 ║DD 1.

אורז. 7

מנקודה א 1להשמיט את הניצב ANעל המטוס א ב ג... קטע קו A 1 Hהוא הגובה.

הבה נבחן כיצד מסודרת המנסרה המשושה (איור 8).

1) משושים שווים מונחים בבסיס א ב ג ד ה וו A 1 B 1 C 1 D 1 E 1 F 1: א ב ג ד ה ו= A 1 B 1 C 1 D 1 E 1 F 1.

2) מטוסים של משושים א ב ג ד ה וו A 1 B 1 C 1 D 1 E 1 F 1הם מקבילים, כלומר הבסיסים מונחים במישורים מקבילים: א ב ג║A 1 B 1 C (α ║ β).

3) משושים א ב ג ד ה וו A 1 B 1 C 1 D 1 E 1 F 1מסודרים כך שכל קצוות הצד מקבילים זה לזה: AA 1 ВВ 1 ... ║FF 1.

אורז. שמונה

הַגדָרָה... אם כל קצה לרוחב ניצב למישור הבסיס, אז מנסרה משושה כזו נקראת קו ישר.

הַגדָרָה... מנסרה ישרה נקראת רגילה אם הבסיסים שלה הם מצולעים רגילים.

שקול מנסרה משולשת רגילה ABCA 1 B 1 C 1.

אורז. תֵשַׁע

מנסרה משולשת ABCA 1 B 1 C 1- נכון, זה אומר שמשולשים רגילים מונחים בבסיסים, כלומר, כל הצדדים של המשולשים האלה שווים. כמו כן, המנסרה הזו היא ישרה. המשמעות היא שקצה הצד ניצב למישור הבסיס. המשמעות היא שכל פנים הצד הם מלבנים שווים.

אז, אם מנסרה משולשת ABCA 1 B 1 C 1- נכון, אם כן:

1) הצלע לרוחב היא בניצב למישור הבסיס, כלומר הגובה: AA 1 ⊥ א ב ג.

2) משולש שווה צלעות מונח בבסיס: ∆ א ב ג- נכון.

הַגדָרָה... שטח הפנים הכולל של המנסרה הוא סכום השטחים של כל פניו. מסומן S מלא.

הַגדָרָה... שטח הפנים לרוחב הוא סכום השטחים של כל הפנים לרוחב. מסומן צד S.

לפריזמה שני בסיסים. אז שטח הפנים הכולל של המנסרה הוא:

S מלא = S צד + 2S ראשי.

שטח המשטח הרוחבי של פריזמה ישרה שווה לתוצר של היקף הבסיס וגובה המנסרה.

ההוכחה תתבצע באמצעות הדוגמה של מנסרה משולשת.

נָתוּן: ABCA 1 B 1 C 1- מנסרה ישרה, כלומר AA 1 ⊥ א ב ג.

AA 1 = h.

לְהוֹכִיחַ: צד S = עיקרי P ∙ ח.

אורז. 10

הוכחה.

מנסרה משולשת ABCA 1 B 1 C 1- ישר, אז AA 1 B 1 B, AA 1 C 1 C, BB 1 C 1 C -מלבנים.

מצא את שטח המשטח הרוחבי כסכום שטחי המלבנים AA 1 B 1 B, AA 1 C 1 C, BB 1 C 1 C:

צד S = AB ∙ h + BC ∙ h + CA ∙ h = (AB + BC + CA) ∙ h = P הראשי ∙ h.

אנחנו מקבלים צד S = P ראשי ∙ h, Q.E.D.

הכרנו את הפולידרה, הפריזמה, זניה. הוכיח את המשפט על פני השטח לרוחב של מנסרה. בשיעור הבא נפתור בעיות באמצעות מנסרה.

1. גֵאוֹמֶטרִיָה. כיתה י'-יא ': ספר לימוד לתלמידי מוסדות חינוך (רמות בסיסיות ופרופיל) / I. M. Smirnova, V. A. Smirnov. - מהדורה חמישית, מתוקנת ומשלימה - ז ': מנמוסינה, 2008. - 288 עמ'. : חולה.
2. גֵאוֹמֶטרִיָה. כיתה י' -י ': ספר לימוד למוסדות חינוך כלליים / שריגין א.פ. - מ': בוסארד, 1999. - 208 עמ ': אי.
3. גֵאוֹמֶטרִיָה. כיתה י ': ספר לימוד למוסדות חינוך עם לימוד מעמיק ומתמחה במתמטיקה / ה. V. Potoskuev, L. I. Zvalich. - מהדורה 6, סטריאוטיפ. - מ ': בוסר, 008.- 233 עמ'. : חולה.

1. יאקלס ().
2. Shkolo.ru ().
3. בית ספר ישן ().
4. WikiHow ().

1. מהו מספר הפנים המינימלי לפריזמה? כמה קודקודים, קצוות יש למנסרה כזו?
2. האם יש מנסרה בעלת 100 קצוות בדיוק?
3. הצלע לרוחב נוטה למישור הבסיס בזווית של 60 °. מצא את גובה המנסרה אם קצה הצד הוא 6 ס"מ.
4. במנסרה משולשת ישרה, כל הקצוות שווים. שטח הפנים הרוחבי שלה הוא 27 ס"מ. מצא את שטח הפנים הכולל של המנסרה.

מנסרות שונות אינן דומות. יחד עם זאת, יש להם הרבה במשותף. כדי למצוא את שטח בסיס המנסרה, עליך להבין איזה סוג יש לה.

תיאוריה כללית

פריזמה היא כל פולידרון שדפנותיו בצורת מקבילית. יתר על כן, כל פולידרון יכול להיות בבסיסו - ממשולש ל- n -gon. יתר על כן, בסיסי המנסרה תמיד שווים זה לזה. זה לא חל על הצדדים הצדדיים - הם יכולים להשתנות במידה ניכרת בגודלם.

בעת פתרון בעיות, לא רק השטח של בסיס המנסרה נתקל. ייתכן שיהיה צורך בידע על המשטח הרוחבי, כלומר כל הפנים שאינן בסיסים. המשטח המלא כבר יהיה האיחוד של כל הפנים המרכיבות את המנסרה.

לפעמים המשימות כוללות גובה. הוא ניצב לבסיסים. האלכסון של פולידרון הוא קטע המחבר בזוגות כל שני קודקודים שאינם שייכים לאותו פנים.

יש לציין כי שטח הבסיס של מנסרה ישרה או נוטה אינו תלוי בזווית בינם לבין פנים הצד. אם יש להם אותן צורות בקצוות העליונים והתחתונים, אזוריהם יהיו שווים.

מנסרה משולשת

יש לו בבסיסו דמות עם שלושה קודקודים, כלומר משולש. ידוע שהוא שונה. אם אז מספיק לזכור ששטחו נקבע על ידי מחצית התוצר של הרגליים.

הסימון המתמטי נראה כך: S = ½ av.

כדי לברר את שטח הבסיס בצורה כללית, הנוסחאות שימושיות: אנפה וזה שבו חצי הצד נלקח לגובה הנמשך אליו.

יש לכתוב את הנוסחה הראשונה כך: S = √ (p (p-a) (p-c) (p-c)). ברשומה זו, יש היקף למחצה (p), כלומר סכום שלושת הצדדים המחולקים לשניים.

שנית: S = ½ n a * a.

אם אתה רוצה לדעת את שטח הבסיס של מנסרה משולשת, שהיא קבועה, אז המשולש מתברר כדו -צדדי. יש נוסחה לזה: S = ¼ a 2 * √3.

מנסרה מרובעת

הבסיס שלו הוא כל אחד מרובעים הידועים. זה יכול להיות מלבן או ריבוע, מקביל או מעוין. בכל מקרה, על מנת לחשב את שטח בסיס המנסרה, יהיה צורך בנוסחה אחרת.

אם הבסיס הוא מלבן, אז שטחו נקבע כך: S = ab, כאשר a, b הם צדי המלבן.

כשמדובר במנסרה מרובעת, שטח הבסיס של מנסרה רגילה מחושב באמצעות הנוסחה לריבוע. כי זה שמתברר שהוא בתחתית. S = 2.

במקרה בו הבסיס הוא מקביל פיפ, יהיה צורך בשוויון הבא: S = a * na. זה קורה כי הצד של המקבילepiped ואחת הפינות ניתנים. לאחר מכן, כדי לחשב את הגובה, יהיה עליך להשתמש בנוסחה נוספת: n a = b * sin A. יתר על כן, הזווית A צמודה לצד "b", והגובה הוא n הפוך לזווית זו.

אם יש מעוין בבסיס המנסרה, אז יהיה צורך באותה נוסחה כדי לקבוע את שטחה כמו במקבילית (מכיוון שזה המקרה המיוחד שלה). אבל אתה יכול גם להשתמש בזה: S = ½ d 1 d 2. כאן d 1 ו- d 2 הם שני אלכסונים של המעוין.

מנסרה מחומשת רגילה

מקרה זה כולל חלוקת המצולע למשולשים, שקל יותר לגלות את אזוריהם. למרות שזה קורה שהנתונים יכולים להיות עם מספר קודקודים אחר.

מכיוון שבסיס המנסרה הוא מחומש רגיל, ניתן לחלק אותו לחמישה משולשים שווה צלעות. אז שטח בסיס המנסרה שווה לשטח של משולש אחד כזה (ניתן לראות את הנוסחה למעלה), מוכפל בחמש.

פריזמה משושה רגילה

על פי העיקרון המתואר לפריזמה מחומשת, ניתן לחלק את משושה הבסיס ל -6 משולשים דו -צדדיים. הנוסחה לאזור הבסיס של מנסרה כזו דומה לזו הקודמת. רק בו יש להכפיל בשישה.

הנוסחה תיראה כך: S = 3/2 ו 2 * √3.

משימות

№ 1. בהינתן קו ישר נכון. האלכסון שלה הוא 22 ס"מ, גובה הפולידרון הוא 14 ס"מ. חשב את שטח בסיס המנסרה והמשטח כולו.

פִּתָרוֹן.בסיס המנסרה הוא ריבוע, אך צדו אינו ידוע. ניתן למצוא את ערכו באלכסון הריבוע (x), הקשור לאלכסון המנסרה (ד) וגובהו (ח). x 2 = d 2 - n 2. מצד שני, קטע זה "x" הוא היפנוטוס במשולש, שרגליו שוות לצד הריבוע. כלומר, x 2 = 2 + a 2. לפיכך, מתברר כי 2 = (d 2 - n 2) / 2.

תחליף 22 במקום d, והחליף את "n" בערך שלו - 14, ואז מתברר שצד הריבוע הוא 12 ס"מ. עכשיו רק גלה את שטח הבסיס: 12 * 12 = 144 ס"מ 2 .

כדי לברר את שטח המשטח כולו, עליך להוסיף את שטח הבסיס פעמיים ולהכפיל את הצד. את האחרון ניתן למצוא בקלות באמצעות הנוסחה למלבן: הכפל את גובה הפולידרון וצד הבסיס. כלומר, 14 ו -12, מספר זה יהיה שווה ל 168 ס"מ 2. שטח הפנים הכולל של המנסרה הוא 960 ס"מ 2.

תשובה.שטח הבסיס של המנסרה הוא 144 ס"מ 2. המשטח כולו 960 ס"מ 2.

Dan 2. דנה בבסיס מונח משולש בעל צלע של 6 ס"מ. במקרה זה, האלכסון של הצד הצדדי הוא 10 ס"מ. חשב את האזורים: בסיס ומשטח צד.

פִּתָרוֹן.מכיוון שהפריזמה קבועה, הבסיס שלה הוא משולש שווה צלעות. לכן שטחו שווה ל 6 בריבוע, כפול ¼ והשורש הריבועי של 3. חישוב פשוט מוביל לתוצאה: 9√3 ס"מ 2. זהו השטח של בסיס אחד של המנסרה.

כל פנים הצד זהים והם מלבנים עם צלעות של 6 ו -10 ס"מ. לחישוב שטחיהם מספיק להכפיל את המספרים הללו. לאחר מכן הכפל אותם בשלוש, כי יש בדיוק כל כך הרבה צדדים בצד של המנסרה. ואז מתברר כי שטח הפנים לרוחב הוא פצע של 180 ס"מ.

תשובה.שטחים: בסיס - 9√3 ס"מ 2, משטח רוחבי של המנסרה - 180 ס"מ 2.

הַגדָרָה.

זהו משושה, שבסיסיו שני ריבועים שווים, ופני הצד הם מלבנים שווים.

צלע צדדיתהוא הצד המשותף של שני פנים צד סמוכים

גובה המנסרההוא קטע בניצב לבסיסי המנסרה

מנסרה אלכסונית- קטע המחבר בין שני קודקודים של הבסיסים שאינם שייכים לאותו פנים

מישור אלכסוני- מישור שעובר באלכסון המנסרה ובקצוות הצדדים שלה

קטע אלכסוני- גבולות צומת המנסרה והמישור האלכסוני. החלק האלכסוני של מנסרה רגילה מרובעת הוא מלבן

קטע מאונך (קטע אורתוגונלי)הוא חיתוך של פריזמה ומישור שצויר בניצב לקצוות הצדדיים שלה

אלמנטים של מנסרה רגילה מרובעת

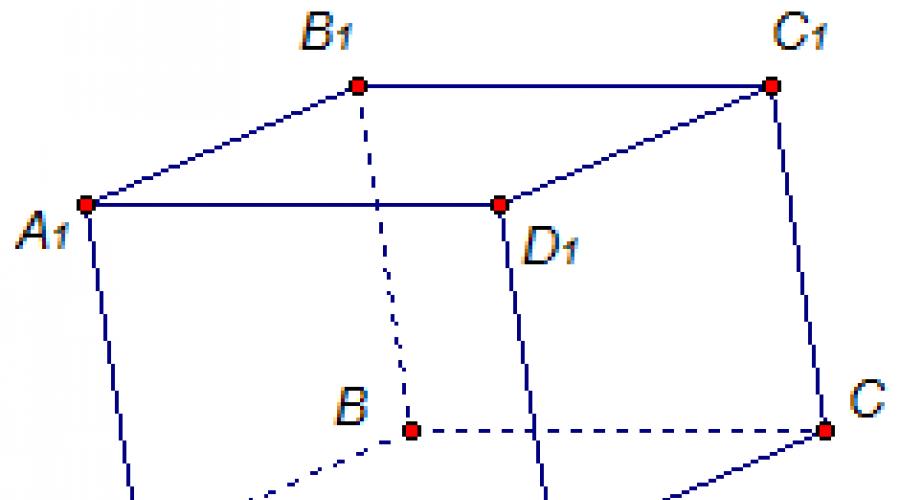
האיור מציג שתי מנסרות מרובעות רגילות, המסומנות באותיות המתאימות:

• בסיסים ABCD ו- A 1 B 1 C 1 D 1 שווים ומקבילים זה לזה
• צדי צד AA 1 D 1 D, AA 1 B 1 B, BB 1 C 1 C ו- CC 1 D 1 D, שכל אחד מהם הוא מלבן.
• משטח צד - סכום השטחים של כל צדי הצד של המנסרה
• משטח מלא - סכום השטחים של כל הבסיסים ופני הצד (סכום השטח של משטח הצד ובסיסים)
• צלעות צד AA 1, BB 1, CC 1 ו- DD 1.
• אלכסוני B 1 D
• בסיס אלכסוני בסיסי
• חתך אלכסוני BB 1 D 1 D
• קטע ניצב A 2 B 2 C 2 D 2.

תכונות של מנסרה רגילה מרובעת

• הבסיסים הם שני ריבועים שווים
• הבסיסים מקבילים זה לזה
• הפנים הצדדיות הן מלבנים
• צדדים שווים זה לזה
• צדי צד ניצבים לבסיסים
• צלעות הצד מקבילות ושוות
• קטע ניצב בניצב לכל קצוות הצד ומקביל לבסיסים
• פינות הקטע הניצב ישרות
• החלק האלכסוני של מנסרה רגילה מרובעת הוא מלבן
• בניצב (חתך אורתוגונלי) במקביל לבסיסים

נוסחאות לפריזמה רגילה מרובעת

הוראות לפתרון בעיות

מנסרה נכונה- מנסרה שבבסיסו מצולע מצולע רגיל, וקצוות הצד בניצב למישור הבסיס. כלומר, מנסרה רגילה מרובעת מכילה בבסיסה כיכר... (ראה מאפיינים לעיל של מנסרה רגילה מרובעת) הערה... זהו חלק מהשיעור עם בעיות גיאומטריה (סטריאומטריה של קטע - פריזמה). להלן המשימות הגורמות לקשיים בפתרון. אם אתה צריך לפתור בעיה בגיאומטריה שאינה כאן, כתוב עליה בפורום. לציון הפעולה של חילוץ שורש ריבועי בפתרונות בעיה, הסמל√ .

משימה.

האלכסון של מנסרה רגילה יוצר משולש זוויתי עם אלכסון הבסיס וגובה המנסרה. בהתאם לכך, על פי משפט פיתגורס, האלכסון של מנסרה רגילה מרובעת נתונה יהיה שווה ל:
√ ((12√2) 2 + 14 2) = 22 ס"מ

תשובה: 22 ס"מ

משימה

פִּתָרוֹן.
מכיוון שיש ריבוע בבסיס מנסרה מרובעת רגילה, נמצא את צלע הבסיס (מסומן כ-) לפי משפט פיתגורס:

A 2 + a 2 = 5 2
2a 2 = 25
א = √12.5

גובה הפנים הצדדי (מסומן כ- h) יהיה אז שווה ל:

H 2 + 12.5 = 4 2
h 2 + 12.5 = 16
h 2 = 3.5
h = √3.5

שטח הפנים הכולל יהיה שווה לסכום שטח הפנים לרוחב וכפול משטח הבסיס

S = 2a 2 + 4ah
S = 25 + 4√12.5 * √3.5
S = 25 + 4√43.75
S = 25 + 4√ (175/4)
S = 25 + 4√ (7 * 25/4)
S = 25 + 10√7 ≈ 51.46 ס"מ 2.

תשובה: 25 + 10√7 ≈ 51.46 ס"מ 2.

הסטריאומטריה היא חלק חשוב בקורס הגיאומטריה הכללית, הבוחן את המאפיינים של דמויות מרחביות. נתון אחד כזה הוא מנסרה מרובעת. במאמר זה נחשוף בפירוט רב יותר את השאלה כיצד לחשב את נפח מנסרה מרובעת.

מהי מנסרה מרובעת?

מן הסתם, לפני מתן הנוסחה לנפח מנסרה מרובעת, יש לתת הגדרה ברורה של דמות גיאומטרית זו. מנסרה כזו מובנת כפולידרון תלת מימדי, המתוחם בשני מרובעים זהים שרירותיים המונחים במישורים מקבילים וארבעה מקבילים.

המרובעים המקבילים המסומנים נקראים בסיסי הדמות, וארבעת המקביליות הן הצדדים. יש להבהיר כאן כי מקביליות הן גם מרובעים, אך לא תמיד הבסיסים הם מקבילים. דוגמה למרובע לא סדיר, שיכול בהחלט להוות בסיס לפריזמה, מוצגת באיור שלהלן.

לכל מנסרה מרובעת יש 6 צדדים, 8 קודקודים ו -12 קצוות. ישנם סוגים שונים של מנסרות מרובעות. לדוגמה, דמות יכולה להיות אלכסונית או ישרה, לא סדירה ונכונה. בהמשך המאמר נראה כיצד ניתן לחשב את נפח מנסרה מרובעת, תוך התחשבות בסוג שלה.

מנסרה אלכסונית עם בסיס לא נכון

זהו הסוג האסימטרי ביותר של מנסרה מרובעת, ולכן חישוב נפחו יהיה קשה יחסית. הביטוי הבא מאפשר לך לקבוע את נפח הדמות:

הסמל So מציין את שטח הבסיס. אם בסיס זה הוא מעוין, מקבילית או מלבן, אז לא קשה לחשב את הערך של So. אז, עבור מעוין ומקבילית, הנוסחה הבאה תקפה:

כאשר a הוא צד הבסיס, הא הוא אורך הגובה שנפל לצד זה מהחלק העליון של הבסיס.

אם הבסיס הוא מצולע לא סדיר (ראה לעיל), אז יש לחלק את שטחו לצורות פשוטות יותר (למשל משולשים), לחשב את שטחיהם ולמצוא את סכומם.

בנוסחת הנפח, h מייצג את גובה המנסרה. זהו אורך הקו הניצב בין שני בסיסים. מכיוון שהפריזמה נוטה, יש לבצע את חישוב הגובה h באמצעות אורך קצה הצד b וזוויות הדיהדרל בין פנים הצד לבסיס.

הדמות הנכונה והנפח שלה

אם הבסיס של מנסרה מרובעת היא ריבוע, והדמות עצמה ישרה, אז היא נקראת רגילה. יש להבהיר כי מנסרה ישרה נקראת כאשר כל צלעותיה לרוחב הם מלבנים וכל אחד מהם בניצב לבסיסים. הנתון הנכון מוצג להלן.

ניתן לחשב את נפחה של מנסרה רגילה מרובעת באמצעות אותה נוסחה כמו נפח דמות לא סדירה. מכיוון שהבסיס הוא ריבוע, שטחו מחושב בפשטות:

גובה המנסרה h שווה לאורכה של הצלע הרוחבית b (צד המלבן). לאחר מכן ניתן לחשב את נפח מנסרה רגילה מרובעת באמצעות הנוסחה הבאה:

מנסרה רגילה עם בסיס מרובע נקראת מקבילה מלבנית. מקבילה זו, במקרה של שוויון הצדדים a ו- b, הופכת לקובייה. נפחו של האחרון מחושב כדלקמן:

הנוסחאות הכתובות לכרך V מצביעות על כך שככל שהסימטריה של הדמות גבוהה יותר, כך נדרשים פחות פרמטרים ליניאריים לחישוב ערך זה. לכן, במקרה של מנסרה נכונה, מספר הפרמטרים הנדרש הוא שניים, ובמקרה של קובייה, אחד.

הבעיה עם הנתון הנכון

לאחר ששקלנו את שאלת מציאת נפח המנסרה המרובעת מנקודת המבט של התאוריה, ניישם את הידע הנצבר בפועל.

זה ידוע שלמקביל רגיל יש אורך אלכסוני בסיסי של 12 ס"מ. אורך האלכסון של הצד הרוחבי שלו הוא 20 ס"מ. יש צורך לחשב את נפח המקביל.

הבה נציין את האלכסון של הבסיס בסמל da, ואת האלכסון של צד הצד באמצעות הסמל db. עבור da האלכסוני, הביטויים הבאים תקפים:

באשר לערך db, הוא האלכסון של מלבן עם הצדדים a ו- b. בשביל זה אתה יכול לכתוב את השוויון הבא:

db2 = a2 + b2 =>

b = √ (db2 - a2)

מחליפים את הביטוי שנמצא לשוויון אחרון, אנו מקבלים:

b = √ (db2 - da2 / 2)

כעת תוכל להחליף את הנוסחאות המתקבלות בביטוי בנפח של דמות רגילה:

V = a2 * b = da2 / 2 * √ (db2 - da2 / 2)

מחליפים את da ו- db במספרים מהצהרת הבעיה, מגיעים לתשובה: V ≈ 1304 cm3.