Как составить аналитическую модель линейной функции. Исследование линейной функции. Защита персональной информации
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Обобщить и систематизировать знания по теме “Линейная функция”:
- закрепить умение читать и строить графики функций, заданных формулами y = kx+b, y = kx;
- закрепить умение определять взаимное расположение графиков линейных функций;
- развивать навыки работы с графиками линейных функций.
Развивать умение анализировать, сравнивать, делать выводы. Развитие познавательного интереса к математике, грамотной устной математической речи, аккуратности и точности при построении.
Воспитание внимательности, самостоятельности в работе, умения работать в паре.
Оборудование: линейка, карандаш, карточки с заданиями, цветные карандаши.
Тип урока: урок закрепления изученного материала.
План урока:
- Организационный момент.
- Устная работа. Математический диктант с самопроверкой и самооценкой. Исторический экскурс.
- Тренировочные упражнения.
- Самостоятельная работа.
- Итог урока.
- Домашнее задание.
Ход урока
1. Сообщение цели урока.
Цель урока – обобщить и систематизировать знания по теме “Линейная функция”.
2. Начнем с проверки ваших теоретических знаний.
– Дайте определение функции. Что такое независимая переменная? Зависимая переменная?
– Дайте определение графика функции.
– Сформулируйте определение линейной функции.
– Что является графиком линейной функции?
– Как построить график линейной функции?
– Сформулируйте определение прямой пропорциональности. Что является графиком? Как построить график? Как расположен в координатной плоскости график функции y = kx при k > 0 и при k < 0?
Математический диктант с самопроверкой и самооценкой.
Рассмотрите рисунки и ответьте на вопросы.
1) График какой функции лишний?
2) На каком рисунке изображен график прямой пропорциональности?
3) На каком рисунке у графика линейной функции отрицательный угловой коэффициент?
4) Определите знак числа b. (Ответ записать в виде неравенства)
Проверка работы. Выставление оценки.
Работа в парах.
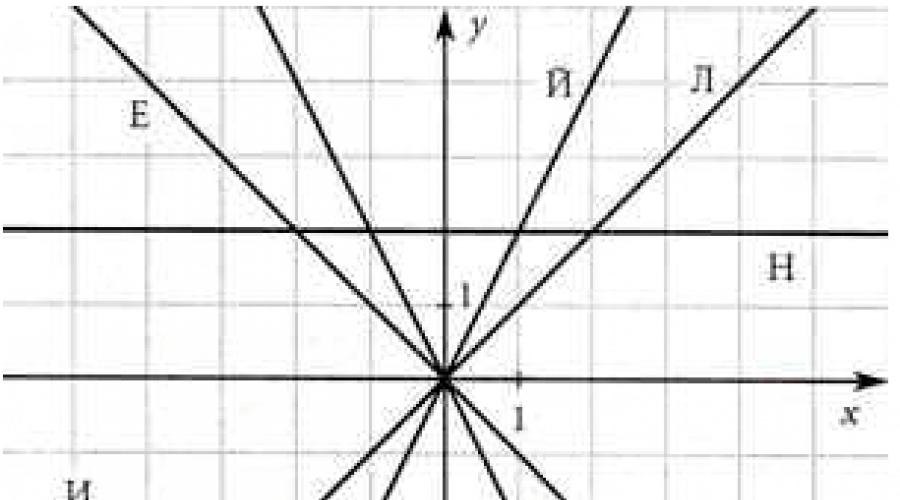
Расшифруйте фамилию математика, который впервые использовал термин функция. Для этого в квадратиках впишите букву, соответствующую графику заданной функции. В оставшийся квадратик впишите букву Ц. Дополните чертеж графиком соответствующей этой букве функции.

Рисунок 1

Рисунок 2

Рисунок 3
Готфрид Вильгельм Лейбниц, 1646-1716 , немецкий философ, математик, физик и языковед. Он и английский ученый И. Ньютон создали (независимо друг от друга) основы важного раздела математики – математического анализа. Лейбниц ввел многие понятия и символы, употребляемые в математике и сейчас.
3. 1. Даны функции, заданные формулами: y = x-5; y = 0,5x; y = – 2x; y = 4.
Назовите функции. Укажите, графики, каких из данных функций пройдут через точку М (8;4). Схематично покажите, каким будет чертеж, если на нем изобразить графики функций, проходящих через точку М.

2. График прямой пропорциональности проходит через точку С (2;1). Составьте формулу, которой задается прямая пропорциональность. При каком значении m график пройдет через точку В (-4;m).
3. Постройте график функции, заданный формулой y=1/2X. Как из графика данной функции можно получить график функции, заданной формулой y=1/2X – 4 и y = 1/2X+3. Проанализируйте полученные графики.
4. Функции заданы формулами:
1) у= 4х+9 и у= 6х-5;
2) у=1/2х-3 и у= 0,5х+2;
3) у= х и у= -5х+2,4;
4) у= 3х+6 и у= -2,5х+6.
Каково взаимное расположение графиков функций? Не выполняя построения, найдите координаты точки пересечения первой пары графиков. (Самопроверка)
4. Самостоятельная работа в парах. (выполняют на мл. бумаге). Межпредметная связь.
Необходимо построить графики функций и выделить ту ее часть, для точек которой выполняется соответствующее неравенство:
у = х + 6, 4 < х < 6; у = -х + 6, -6 < х < -4; у = – 1/3 х + 10, -6 < х < -3; у = 1/3 х +10, 3 < х < 6; у = -х + 14, 0 < х < 3; у = х + 14, -3 < х < 0; у = 9х – 18, 2 < х < 4; у = – 9х – 18 -4 < х < -2; у = 0, -2 < х < 2.
Какой рисунок получился? (Тюльпан .)

Немного о тюльпанах:
Известно около 120 видов тюльпанов, распространенных, главным образом в Средней, Восточной и Южной Азии и Южной Европе. Ботаники считают, что культура тюльпанов возникла в Турции в ХII столетии Мировую славу растение обрело вдали от своей родины, в Голландии, по праву названной Страной тюльпанов.
Вот легенда о тюльпане. В золотистом бутоне желтого тюльпана было заключено счастье. До этого счастья никто не мог добраться, ибо не было такой силы, которая смогла бы открыть его бутон. Но однажды по лугу шла женщина с ребенком. Мальчик вырвался из рук матери, со звонким смехом подбежал к цветку, и золотистый бутон раскрылся. Беззаботный детский смех совершил то, чего не смогла сделать никакая сила. С тех пор и повелось дарить тюльпаны только тем, кто испытывает счастье.
Творческое домашнее задание. Создать рисунок в прямоугольной системе координат, состоящий из отрезков и составить его аналитическую модель.
6. Самостоятельная работа. Дифференцированное задание (в двух вариантах)
I вариант:
Изобразите схематично графики функций:

II вариант:
Изобразите схематично графики функций, для которых выполнены условия:

7. Итог урока
Анализ проделанной работы. Выставление оценок.
Инструкция
Чтобы найти координаты точки, принадлежащей прямой, выберите ее на линии и опустите перпендикулярные линии на оси координат. Определите, какому числу соответствует точка пересечения, пересечение с осью ох – это значение абсциссы, то есть х1, пересечение с осью оу - это ордината, у1.
Постарайтесь выбрать точку, координаты которой можно определить без дробных значений, для удобства и точности расчетов. Для построения уравнения вам нужно как минимум две точки. Найдите координаты еще одной точки, принадлежащей данной прямой (х2, у2).
Подставьте значения координат в уравнение прямой, имеющей общий вид у=kx+b. У вас получится система из двух уравнений у1=kx1+b и y2=kx2+b. Решите эту систему, например, следующим способом.
Выразите b из первого уравнения и подставьте во второе, найдите k, подставьте в любое уравнение и найдите b. Например, решение системы 1=2k+b и 3=5k+b будет выглядеть так: b=1-2k, 3=5k+(1-2k); 3k=2, k=1.5, b=1-2*1,5=-2. Таким образом, уравнение прямой имеет вид y=1,5х-2.
Зная две точки, принадлежащие прямой, попробуйте воспользоваться каноническим уравнением прямой, оно выглядит таким образом: (х - х1)/(х2 - х1)=(у - у1)/(у2 - у1). Подставьте значения (х1;у1) и (х2;у2), упростите. Например, точки (2;3) и (-1;5) принадлежат прямой (х-2)/(-1-2)=(у-3)/(5-3); -3(х-2)=2(у-3); -3х+6=2у-6; 2у=12-3х или у=6-1,5х.
Чтобы найти уравнение функции, имеющей нелинейный график, действуйте так. Просмотрите все стандартные графики y=x^2, y=x^3, y=√x, y=sinx, y=cosx, y=tgx и т.д. Если один из них напоминает вам ваш график, возьмите его за основу.
Начертите на той же оси координат стандартный график функции-основы и найдите его от своего графика. Если график перенесен на несколько единиц вверх или вниз – значит к функции добавлено это число (например, у=sinx+4). Если график перенесен вправо или влево, значит, число добавлено к аргументу (например, у=sin (х+П/2).
Вытянутый график в высоту график говорит о том, что функция аргумента умножена на какое-то число (например, у=2sinx). Если график, напротив, уменьшен в высоту, значит, число перед функцией меньше 1.
Сравните график функции-основы и вашей функции по ширине. Если он более узкий, значит перед х стоит число больше 1, широкий – число меньше 1 (например, у=sin0.5х).
Обратите внимание
Возможно, график соответствует найденному уравнению лишь на определенном отрезке. В таком случае укажите, для каких значений х выполняется полученное равенство.
Прямая - алгебраическая линия первого порядка. В декартовой системе координат на плоскости уравнение прямой задается уравнением первой степени.
Вам понадобится
- Знания по аналитической геометрии. Базовые знания по алгебре.
Инструкция
Уравнение задается двух на , которые эта прямая должна пройти. Составим соотношение координат этих точек. Пусть первая точка имеет координаты (x1,y1), а вторая (x2,y2), тогда уравнение прямой запишется следующим образом: (x-x1)/(x2-x1) = (y-y1)(y2-y1).
Преобразуем полученное уравнение прямой и выразим явно y через x. После этой операции уравнение прямой примет окончательный вид: y=(x-x1)/((x2-x1)*(y2-y1))+y1.
Видео по теме
Обратите внимание
Если одно из чисел в знаменателе равно нулю значит, что прямая параллельна одной из осей координат.
Полезный совет
После того как вы составили уравнение прямой, проверьте его правильность. Для этого подставьте координаты точек вместо соответствующих координат и убедитесь, что выполняется равенство.
Часто известно, что y зависит от x линейно, и дан график этой зависимости. В этом случае возможно узнать уравнение прямой. Сначала нужно выбрать на прямой две точки.

Инструкция
Найдите выбранных точек. Для этого опустите перпендикуляры от точек на оси координат и запишите цифры со шкалы. Так для точки B из нашего примера координата x равна -2, а координата y - 0. Аналогичным образом для точки А координаты будут (2;3).
Известно, что прямой имеет вид y = kx + b. Подставляем в уравнение в общем виде координаты выбранных точек, тогда для точки A получим такое уравнение: 3 = 2k +b. Для точки B получим другое уравнение: 0 = -2k + b. Очевидно, что у нас система из двух уравнений с двумя неизвестными: k и b.
Дальше решаем систему любым удобным способом. В нашем случае можно сложить уравнения системы, так как неизвестная k входит в оба уравнения с коэффициентами, которые одинаковы по модулю, но противоположны по знаку. Тогда получим 3 + 0 = 2k - 2k + b + b, или, что то же: 3 = 2b. Таким образом b = 3/2. Подставим найденное значение b в любое из уравнений, чтобы найти k. Тогда 0 = -2k + 3/2, k = 3/4.
Подставим найденные k и b в уравнение общего вида и получим искомое уравнение прямой: y = 3x/4 + 3/2.
Видео по теме
Обратите внимание
Коэффициент k называется угловым коэффициентом прямой и равен тангенсу угла между прямой и осью x.
Прямую линию можно построить по двум точкам. Координаты этих точек «спрятаны» в уравнении прямой. Уравнение расскажет о линии все секреты: как повернута, в какой стороне координатной плоскости располагается и т.д.

Инструкция
Чаще требуется строить в плоскости. У каждой точки будет две координаты: х, y. Обратите внимание на уравнение , оно подчиняется общему виду: y=k*x ±b, где k, b - свободные числа, а y, х – те самые координаты всех точек прямой.Из уравнения общего вида , что для нахождения координаты y надо знать координату х. Самое интересное, что значение координаты х можно выбрать любое: из всей бесконечности известных чисел. Далее подставьте х в уравнение и, решив его, найдите у. Пример. Пусть дано уравнение: у=4х-3. Придумайте два любых значения для координат двух точек. К примеру, х1 = 1, х2 = 5.Подставьте эти значения в уравнения для нахождения координат у. у1 = 4*1 – 3 = 1. у2 = 4*5 – 3 = 17. Получились две точки А и В, А (1; 1) и В (5; 17).
Следует построить найденные точки в координатной оси, соединить их и увидеть ту самую прямую, которая была описана уравнением. Для построения прямой необходимо работать в декартовой системе координат. Начертите оси Х и У. В точке пересечения поставьте значение «ноль». Нанесите числа на оси.
В построенной системе отметьте две найденные в 1-м шаге точки. Принцип выставления указанных точек: точка А имеет координаты х1 = 1, у1 = 1; на оси Х выберите число 1, на оси У – число 1. В этой точке и находится точка А.Точка В задана значениями х2 = 5, у2 = 17. По аналогии найдите точку В на графике. Соедините А и В, чтобы получилась прямая.
Видео по теме
Термин решения функции как таковой в математике не используется. Под данной формулировкой следует понимать выполнение некоторых действий над заданной функцией с целью нахождения какой-то определенной характеристики, а также выяснение необходимых данных для построения графика функции.

Инструкция
Можно рассмотреть примерную схему, по которой целесообразно поведение функции и строить ее график.
Найдите область определения функции. Определите, является ли функция четной и нечетной. В случае нахождения нужного ответа, продолжите только на требуемой полуоси. Определите, является ли функция периодической. В случае положительного ответа продолжите исследование только на одном периоде. Найдите точки и определите ее поведение в окрестности этих точек.
Найдите точки пересечения графика функции с осями координат. Найдите , если они есть. Исследуйте с помощью первой производной функцию на экстремумы и интервалы монотонности. Также проведите исследование с помощью второй производной на выпуклость, вогнутость и точки перегиба. Выберите точки для уточнения функции и вычислите в них значения функции. Постройте график функции, учитывая полученные результаты по всем проведенным исследованиям.
На оси 0Х следует выделить характерные точки: точки разрыва, х=0 , нули функции, точки экстремума, точки перегиба. В этих асимптот, и даст эскиз графика функции.
Так, на конкретном примере функции y=((x^2)+1)/(x-1) проведите исследование с помощью первой производной. Перепишите функцию в виде y=x+1+2/(x-1). Первая производная будет равна y’=1-2/((x-1)^2).
Найдите критические точки первого рода: y’=0, (x-1)^2=2, в результате получатся две точки: x1=1-sqrt2, x2=1+sqrt2. Отметьте полученные значения на области определения функции (рис. 1).
Определите знак производной на каждом из интервалов. На основе правила чередования знаков от «+» к «-» и от «-» к «+», получите, что точка максимума функции x1=1-sqrt2, а точка минимума x2=1+sqrt2. Этот же вывод можно сделать и по знаку второй производной.
Класс: 7
Функция занимает одно из ведущих мест в школьном курсе алгебры и имеет многочисленные приложения в других науках. В начале изучения, с целью мотивации, актуализации вопроса сообщаю, что ни одно явление, ни один процесс в природе не могут быть изучены, никакая машина не может быть сконструирована, а затем действовать без полного математического описания. Одним из инструментом для этого является функция. Её изучение начинается в 7-м классе, как правило, дети не вникают в определение. Особенно труднодоступными понятиями являются такие как область определения и область значения. Используя, известные связи между величинами в задачах на движение, стоимости перекладываю их на язык функции, удерживая связь с её определением. Таким образом, у учащихся понятие функции формируется на осознанном уровне. На этом же этапе ведётся кропотливая работа над новыми понятиями: область определения, область значения, аргумент, значение функции. Использую опережающее обучение: ввожу обозначения D(у), Е(у), знакомлю с понятием нуля функции (аналитически и графически), при решении упражнений с участками знакопостоянства. Чем раньше и чаще учащиеся встречаются с трудными понятиями, тем лучше их осознают на уровне долговременной памяти. При изучении линейной функции целесообразно показать связь с решением линейных уравнений и систем, а позднее с решением линейных неравенств и их систем. На лекции учащиеся получают большой блок (модуль) новой информации, поэтому в конце лекции материал " отжимается" и составляется конспект, который учащиеся должны знать. Практические навыки отрабатываются в процессе выполнения упражнений с применением различных методов, в основе которых индивидуальная и самостоятельная работа.
1. Некоторые сведения о линейной функции.
Линейная функция очень часто встречается в практической деятельности. Длина стержня является линейной функцией температуры. Длина рельсов, мостов также является линейной функцией температуры. Расстояние, пройденное пешеходом, поездом, автомашиной при постоянной скорости движения, – линейные функции времени движения.
Линейная функция описывает ряд физических зависимостей и законов. Рассмотрим некоторые из них.
1) l = l о (1+at) – линейное расширение твёрдых тел.
2) v = v о (1+bt) – объёмное расширение твёрдых тел.
3) p=p о (1+at) – зависимость удельного сопротивления твёрдых проводников от температуры.
4) v = v о + at – скорость равноускоренного движения.
5) x= x о + vt – координата равномерного движения.
Задача 1. Определите линейную функцию по табличным данным:
| х | 1 | 3 |
| у | -1 | 3 |
Решение. у= kx+b, задача сводится к решению системы уравнений: 1=k 1+b и 3=k 3 + b
Ответ: у = 2х – 3.
Задача 2. Двигаясь равномерно и прямолинейно, тело прошло за первые 8с 14м, а ещё за 4с – 12 м. Составьте по этим данным уравнение движения.
Решение. По условию задачи имеем два уравнения: 14= х о +8 v о и 26=х о +12 v о, решая систему уравнений, получаем v=3, х о =-10.
Ответ: х = -10 + 3t.
Задача 3. Из города вышел автомобиль, движущийся со скоростью 80км/ч. Через 1,5 ч вдогонку ему выехал мотоцикл, скорость которого 100 км/ч. Через сколько времени мотоцикл его догонит? На каком расстоянии от города это произойдёт?
Ответ: 7,5ч, 600км.
Задача 4. Расстояние между двумя точками в начальный момент 300м. Точки движутся навстречу друг другу со скоростями 1,5 м/с и 3,5м/с. Когда они встретятся? Где это произойдёт?
Ответ: 60 с, 90 м.
Задача 5. Медная линейка при 0 о С имеет длину 1м. Найдите увеличение её длины при повышении её температуры на 35 о, на 1000 о С (температура плавления меди 1083 о С)
Ответ:0,6мм.
2. Прямая пропорциональность.
Многие законы физики выражаются через прямую пропорциональность. В большинстве случаев для записи этих законов используется модель
в отдельных случаях –
Приведём несклько примеров.
1. S = v t (v – const)
2. v = a t (a – const, a – ускорение).
3. F = kx (закон Гука:F – сила, к– жёсткость(const), х– удлинение).
4. Е= F/q (Е– напряженность в данной точке электрического поля, Е – const, F– сила, действующая на заряд, q – величина заряда).
В качестве математической модели прямой пропорциональности можно использовать подобие треугольников или пропорциональность отрезков (теорема Фалеса).
Задача 1. Поезд проехал мимо светофора за 5 с, а мимо платформы длиной 150 м, за 15 с. Каковы длина поезда и его скорость?
Решение. Пусть х – длина поезда, х+150 – суммарная длина поезда и платформы. В данной задаче скорость постоянна, а время пропорционально длине.
Имеем пропорцию: (х+150) :15 = х: 5.
Откуда х = 75, v = 15.
Ответ. 75 м, 15 м/с.
Задача 2. Катер прошел по течению 90 км за некоторое время. За то же время он прошел бы против течения 70 км. Какое расстояние за это время проплывет плот?
Ответ. 10 км.
Задача 3. Какова была первоначальная температура воздуха, если при нагревании на 3 градуса его обьём увеличился на 1% от первоначального.
Ответ. 300 К (Кельвин) или 27 0 С.
Лекция по теме "Линейная функция".
Алгебра, 7 класс
1. Рассмотрим примеры задач с применением известных формул:
S = v·t (формула пути), (1)
С = ц·к (формула стоимости). (2)
Задача 1. Автомобиль отъехав от пункта А на расстояние 20км продолжил свой путь со скоростью 62 км/ч. На каком расстояние от пункта А будет находиться автомобиль через t часов? Составьте выражение к задаче, обозначив расстояние S, найдите его при t = 1ч, 2,5 ч, 4ч.
1) Используя формулу (1) найдём путь, пройденный
автомобилем со скоростью 62 км/ч за время t, S 1
= 62t;
2) Тогда от пункта А через t часов автомобиль
будет находиться на расстояние S = S 1 + 20
или S = 62t + 20, найдём значение S:
при t = 1, S = 62*1 + 20,
S = 82;
при t = 2,5, S = 62*2,5 + 20, S = 175;
при t = 4, S = 62*4+
20, S = 268.
Замечаем, что при нахождении S меняется только значение t и S, т.е. t и S – переменные, причём S зависит от t, каждому значению t соответствует единственное значение S. Обозначив, переменную S за Y, а t за x, получим формулу для решения данной задачи:
Y= 62х + 20. (3)
Задача 2. В магаине купили учебник за 150 рублей и 15 тетрадей по n рублей. Сколько денег уплатили за покупку? Составьте выражение к задаче, обозначив стоимость С, найдите его при n = 5,8,16.
1) Используя формулу (2) найдём стоимость
тетрадей С 1 = 15n;
2) Тогда стоимость всей покупки С= С 1 +150
или С= 15n+150, найдём значение C:
при n = 5, С = 15 5 + 150,
С= 225;
при n = 8, С = 15 8 + 150,
С= 270;
при n = 16, С = 15 16+
150, С= 390.
Аналогично, замечаем, что С и n переменные, для каждого значения n соответствует единственное значение С. Обозначив, переменную С за Y, а n за x, получим формулу для решения задачи 2:
Y= 15х + 150. (4)
Сравнивая формулы (3) и (4) убеждаемся, что переменная Y находится через переменную х по одному алгоритму. Мы рассмотрели лишь две разные задачи, описывающие окружающие нас явления каждый день. На самом деле процессов, изменяющих по полученным законам – множество, поэтому такая зависимость между переменными заслуживает изучение.
Решения задач показывают, что значения переменной х выбраны произвольно, удовлетворяющие условиям задач (положительные в задаче 1 и натуральные в задаче 2), т. е. х – независимая переменная (её называют аргументом), а Y – зависимая переменная и между ними однозначное соответствие, а по определению такая зависимость является функцией. Следовательно, обозначив коэффициент при х буквой k, а свободный член буквой b, получим формулу
Y= kx + b.
Определение.Функция вида y= kx + b , где k, b – некоторые числа, х - аргумент, y– значение функции, называется линейной функцией.
Для изучения свойств линейной функции введём определения.
Определение 1. Множество допустимых значений независимой переменной, называется областью определения функции (допустимые – это значит те числовые значения х при которых выполняются вычисления y) и обозначается D(у).
Определение 2. Множество значений зависимой переменной, называется областью значения функции (это те числовые значения, которые принимает y) и обозначается Е(у).
Определение 3. Графиком функции называется множество точек координатной плоскости, координаты которых обращают формулу в верное равенство.
Определение 4. Коэффициент k при х называется угловым коэффициентом.
Рассмотрим свойства линейной функции.
1. D(у) – все числа (умножение определено на
множестве всех чисел).
2. Е(у) – все числа.
3. Если y = 0, то х = -b/k, точка (-b/k;0) – точка
пересечения с осью Ох, называется нулём функции.
4. Если х= 0, то y= b, точка (0;b) – точка
пересечения с осью Оу.
5. Выясним, в какую линию выстроит точки
линейная функция на координатной плоскости, т.е.
что является графиком функции. Для этого
рассмотрим функции
1) y= 2x + 3, 2) y= -3x – 2.
Для каждой функции составим таблицу значений. Зададим произвольные значения переменной х, и вычислим соответствующие значения переменной Y.
| х | -1,5 | -2 | 0 | 1 | 2 |
| Y | 0 | -1 | 3 | 5 | 7 |

Построив полученные пары (х;y) на координатной плоскости и соединяя их для каждой функции отдельно (мы взяли значения х с шагом 1, если уменьшить шаг, то точки выстроятся чаще, а если шаг будет близок к нулю, то точки сольются в сплошную линию), замечаем, что точки выстраиваются в прямую линию в случае 1) и в случае 2). В силу того, что функции выбраны произвольно (постройте самостоятельно графики y= 0,5x – 4, y= x + 5), сделаем вывод, что графиком линейной функции является прямая . Используя свойство прямой: через две точки проходит единственная прямая, достаточно для построения прямой взять две точки.
6.Из геометрии известно, что прямые могут либо пересекаться, либо быть параллельными. Исследуем взаимное расположение графиков нескольких функций.
1) y= -x + 5, y= -x + 3, y= -x – 4; 2) y= 2x + 2, y= x + 2, y= -0,5x + 2.
Построим группы графиков 1) и 2) и сделаем выводы.
|
 |
Графики функций 1) расположились параллельно, исследуя формулы, замечаем, что все функции имеют одинаковые коэффициенты при х.
Графики функций 2) пересеклись в одной точке (0;2). Исследуя формулы, замечаем, что коэффициенты различны, а число b = 2.
Кроме этого, нетрудно заметить, что прямые, заданные линейными функциями с k › 0 образуют с положительным направлением оси Ох – острый угол, с k ‹ 0 тупой угол. Поэтому коэффициент k называется угловым коэффициентом.
7. Рассмотрим частные случаи линейной функции, в зависимости от коэффициентов.
1) Если b=0, то функция принимает вид y= kx, тогда k = y/х (отношение показывает, во сколько раз отличается или какую часть составляет y от х).
Функцию вида Y= kx, называют прямой пропорциональностью. Эта функция обладает всеми свойствами линейной функции, её особенностью является то, что при х=0 y=0. График прямой пропорциональности проходит через начало координат точку (0;0).
2) Если k = 0, то функция принимает вид y = b, что означает, при любых значениях х функция принимает одно и то же значение.
Функцию вида y = b, называют постоянной. Графиком функции является прямая проходящая через точку (0;b) параллельно оси Ох, при b=0 график постоянной функции совпадает с осью абсцисс.
Конспект
1. Определение Функция видаY= kx + b, где k, b – некоторые числа, х -аргумент, Y– значение функции, называется линейной функцией.
D(у) – все числа.
Е(у) – все числа.
Графиком линейной функции является прямая, проходящая через точку (0;b).
2. Если b=0,то функция принимает вид y= kx, называется прямой пропорциональностью. График прямой пропорциональности проходит через начало координат.
3. Если k = 0, то функция принимает вид y= b, называется постоянной. График постоянной функции проходит через точку (0;b), параллельно оси абсцисс.
4. Взаимное расположение графиков линейных функций.
Даны функции y= k 1 x + b 1 и y= k 2 x + b 2.
Если k 1 = k 2 , то графики параллельны;
Если k 1 и k 2 не равны, то графики пересекаются.
5. Примеры графиков линейных функций см. выше.
Литература.
- Учебник Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и другие. “Алгебра, 8”.
- Дидактические материалы по алгебре для 8 класса / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. – М.: Просвещение, 2006. – 144 с.
- Приложение к газете 1 сентября “Математика”, 2001 г., №2, №4.
Маслова Ангелина
Исследовательская работа по математике. Ангелина составила компьютерную модель линейной функции, с помощью которой проводила исследование.
Скачать:
Предварительный просмотр:
Муниципальное автономное образовательное учреждение средняя школа №8 городского округа г.Бор Нижегородской области
Исследовательская работа по информатике и математике
Выполнила ученица 7А класса, Маслова Ангелина
Руководитель: учитель информатики, Воронина Анна Алексеевна.
Городской округ г.Бор – 2015г.
Введение
- Исследование линейной функции в электронных таблицах
Заключение
Список литературы
Введение
В этом году на уроках алгебры мы познакомились с линейной функцией. Мы учились строить график линейной функции, определяли, как должен вести себя график функции в зависимости от ее коэффициентов. Чуть позже, на уроке информатики мы узнали, что эти действия можно считать математическим моделированием. Я решила проверить, можно ли исследовать линейную функцию с помощью электронных таблиц.
Цель работы: исследовать линейную функцию в электронных таблицах
Задачи исследования:
- найти и изучить информацию о линейной функции;
- построить математическую модель линейной функции в электронной таблице;
- исследовать линейную функцию с помощью построенной модели.
Объект исследования: математическое моделирование.
Предмет исследования: математическая модель линейной функции.
Моделирование как метод познания
Человек познает мир почти с самого своего рождения. Для этого человек использует модели, которые могут быть самыми разнообразными.
Модель – это новый объект, который отражает некоторые существенные свойства реального объекта.
Модели реальных объектов используются в самых разных ситуациях:
- Когда объект очень большой (например Земля – модель: глобус или карта) или,наоборот, слишком маленький (биологическая клетка).
- Когда объект очень сложен по своему строению (автомобиль – модель: детская машинка).
- Когда объект опасен для изучения (вулкан).
- Когда объект находится очень далеко.
Моделирование – это процесс создания и изучения модели.
Мы сами создаем и используем модели, даже порой не задумываясь об этом. Например, мы делаем фотографии какого-нибудь события в нашей жизни, а потом показываем их своим друзьям.
По типу информации все модели можно разделить на несколько групп:
- Словесные модели. Эти модели могут существовать в устной или письменной форме. Это может быть просто словесное описание какого-нибудь предмета или стихотворение, а может быть статья в газете или сочинение – все это словесные модели.
- Графические модели. Это наши рисунки, фотографии, схемы и графики.
- Знаковые модели. Это модели, записанные на каком-либо знаковом языке: ноты, математические, физические или химические формулы.
Линейная функция и ее свойства
Линейной функцией называется функция вида
Графиком линейной функции является прямая линия.
1 . Чтобы построить график функции , нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.
Например, чтобы построить график функции , удобно взять и , тогда ординаты этих точек будут равны и .
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции :

2 . В уравнении функции y=kx+b коэффициент k отвечает за наклон графика функции:
Коэффициент b отвечает за сдвиг графика вдоль оси OY:
На рисунке ниже изображены графики функций ; ;

Заметим, что во всех этих функциях коэффициент больше нуля вправо . Причем, чем больше значение , тем круче идет прямая.
Во всех функциях – и мы видим, что все графики пересекают ось OY в точке (0;3)
Теперь рассмотрим графики функций ; ;

На этот раз во всех функциях коэффициент меньше нуля , и все графики функций наклонены влево . Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)
Рассмотрим графики функций ; ;

Теперь во всех уравнениях функций коэффициенты равны. И мы получили три параллельные прямые.
Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции (b=3) пересекает ось OY в точке (0;3)
График функции (b=0) пересекает ось OY в точке (0;0) - начале координат.
График функции (b=-2) пересекает ось OY в точке (0;-2)
Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции .
Если k 0 , то график функции имеет вид:

Если k>0 и b>0 , то график функции имеет вид:

Если k>0 и b , то график функции имеет вид:

Если k, то график функции имеет вид:

Если k=0 , то функция превращается в функцию и ее график имеет вид:

Ординаты всех точек графика функции равны
Если b=0 , то график функции проходит через начало координат:

4. Условие параллельности двух прямых:
График функции параллелен графику функции , если
5. Условие перпендикулярности двух прямых:
График функции перпендикулярен графику функции , если или
6 . Точки пересечения графика функции с осями координат.
С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда . То есть точка пересечения с осью OX имеет координаты (;0):

Исследование линейной функции в электронных таблицах
Для исследования линейной функции в среде электронных таблиц я составила следующий алгоритм:
- Построить математическую модель Линейной функции в электронной таблице.
- Заполнить трассировочную таблицу значений аргумента и функции.
- Построить график Линейной функции с помощью мастера диаграмм.
- Исследовать Линейную функцию в зависимость от значений коэффициентов.
Для исследования линейной функции я воспользовалась программой Mikсrosoft Office Excel 2007. Для составления таблиц значений аргументов и функций я использовала формулы. У меня получилась следующая таблица значений:
На такой математической модели, можно легко проследить за изменениям графика линейной функции, меняя значения коэффициентов в таблице.
Также с помощью электронных таблиц, я решила проследить за тем, как меняется взаимное расположение графиков двух линейных функций. Построив новую математическую модель в электронной таблице, я получила следующий результат:
Меняя коэффициенты двух линейных функций я наглядно убедилась в справедливости изученной информации о свойствах линейных функций.
Заключение
Линейная функция в алгебре считается самой простой. Но при этом она имеет много свойств, которые не сразу становятся понятны. Построив математическую модель линейной функции в электронных таблицах, и исследовав ее, мне стали более понятны свойства линейной функции. Я наглядно смогла убедиться в том, как меняется график при изменении коэффициентов функции.
Я думаю, что построенная мной математическая модель поможет ученикам седьмых классов самостоятельно исследовать линейную функцию и лучше ее понять.
Список литературы
- Учебник алгебры для 7 класса.
- Учебник информатики для 7 класса
- Wikipedia.org
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Объект исследования: линейная функция. Предмет исследования: математическая модель линейной функции.
Цель работы: исследовать линейную функцию в электронных таблицах Задачи исследования: найти и изучить информацию о линейной функции; построить математическую модель линейной функции в электронной таблице; исследовать линейную функцию с помощью построенной модели.
Линейной функцией называется функция вида y= k x+ b , где х является аргументом, а k и b – некоторые числа (коэффициенты) Графиком линейной функции является прямая линия.
Рассмотрим функцию y=kx+b такую, что k 0 , b=0 . Вид: y=kx В одной системе координат построим графики данных функций: y=3x y=x y=-7x Каждый график строим соответствующим цветом х 0 1 у 0 3 х 0 1 у 0 1 х 0 1 у 0 7
График линейной функции вида у= k х проходит через начало координат. y=x y=3x y=-7x у х
Вывод: График линейной функции вида y = kx + b пересекает ось О Y в точке (0; b).
Рассмотрим функцию y=kx+b , где k=0. Вид: y=b В одной системе координат построить графики функций: y=4 y=-3 y=0 Каждый график строим соответствующим цветом
График линейной функции вида y = b проходит параллельно оси ОХ и пересекает ось О Y в точке (0; b). y=4 y=-3 y=0 у х
В одной системе координат построить графики функций: Y=2x Y=2x+ 3 Y=2x-4 Каждый график строим соответствующим цветом х 0 1 у 0 2 х 0 1 у 3 5 х 0 1 у -4 -2
Графики линейных функций вида y=kx+b параллельны, если коэффициенты при х одинаковы. у =2x+ 3 у =2x у =2x-4 у х
В одной системе координат построим графики функций: y=3x+4 Y= - 2x+4 Графики строим соответствующим цветом х 0 1 у 4 7 х 0 1 у 4 2
Графики двух линейных функций вида y=kx+b пересекаются, если коэффициенты при х – различны. у х
В одной системе координат построим графики функций: y=0 , 5x-2 y=-2x-4 y= 4 x-1 y=- 0, 2 5 x- 3 х 0 4 у х 0 -2 у -4 0 х 0 4 у -2 0 х 0 1 у -1 3 х 0 - 4 у -3 -2
y=0 , 5x-2 y=-2x-4 y= 4 x-1 y=- 0, 2 5 x- 3 Графики двух линейных функций вида y=kx+b взаимно перпендикулярны, если произведение коэффициентов при х равно « -1» .
Поэтому коэффициент k называют угловым коэффициентом прямой – графика функции y=kx+ b . Если k 0 , то угол наклона графика к оси О X острый. Функция возрастает. у х у х
Электронная таблица
Электронная таблица
Линейные уравнения Алгебраическое условие Геометрический вывод y = к 1 х+ b 1 к 1 = к 2 , b 1 ≠ b 2 y = к 2 х+ b 2 к 1 = к 2, b 1 = b 2 к 1 ≠ к 2 к 1 * к 2 = -1 Прямые параллельны Прямые совпадают Прямые перпендикулярны Прямые пересекаются
построенная мной математическая модель поможет ученикам седьмых классов самостоятельно исследовать линейную функцию и лучше ее понять.

