Upotreba procesa čiste reprodukcije. Proces čiste reprodukcije. Procesi uzgoja i smrti
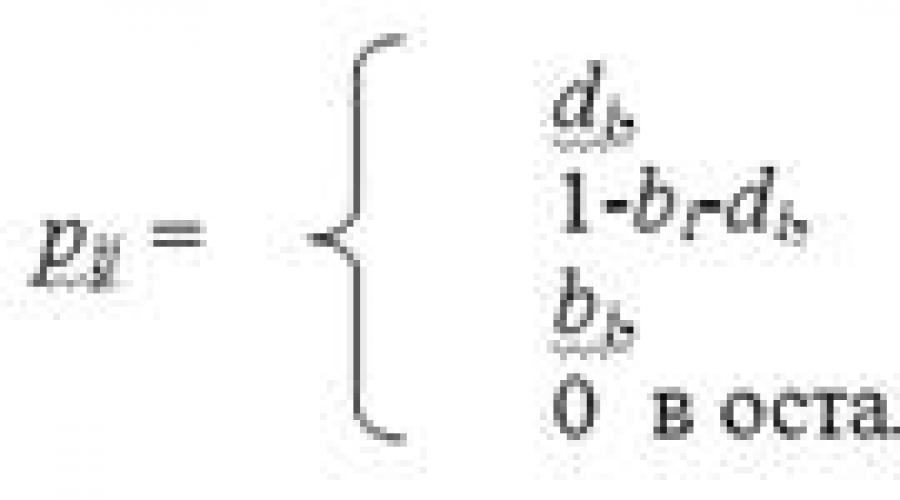
Uvođenje
U ovom radu, shema kontinuiranih Markovskog lanca razmatrat će se - takozvani "dijagram smrti i reprodukcije"
Proces reprodukcije i smrti je slučajni proces sa brojevima (konačnim ili beskonačnim) setom država koji teče u diskretnom ili neprekidnom vremenu. To je da neki sistem nasumičnim trenucima vremena prolazi iz jedne države u drugu, a prelazi između država nastaju sa skokom kada se događaju neki događaji. U pravilu su ovi događaji dvije vrste: jedan od njih uvjetno se naziva rođenje nekih predmeta, a druga je smrt ovog objekta.
Ova je tema izuzetno relevantna zbog velike važnosti Markovskog procesa u istraživanju ekonomskih, ekoloških i bioloških procesa, osim Markovskog procesa na srcu teorije masovne usluge, koji se trenutno aktivno koristi u različitim ekonomskim područjima, uključujući upravljanje procesima u preduzeću.
Markov procesi smrti i reprodukcije široko se koriste u objašnjavanju različitih procesa koji se javljaju u fizici, biosferi, ekosustavu itd. Treba napomenuti da je ova vrsta Markov procesa precizno primila svoje ime zbog široko rasprostranjene upotrebe u biologiji, posebno kada modeliranje smrti i reprodukcije pojedinca raznih populacija.
Ovaj rad će biti zadatak, čija je svrha definirati matematička očekivanja za neke procese uzgoja i smrti. Primjeri proračuna prosječnog broja prijava u sustavu u stacionarnom režimu i procjene vrše se za različite slučajeve uzgoja i procesa smrti.
Procesi uzgoja i smrti
Procesi reprodukcije i smrti posebni su slučaj Markov slučajnih procesa, koji se, ipak, vrlo široko koriste u proučavanju diskretnih sistema sa stohastičnom prirodom funkcioniranja. Proces reprodukcije i smrti je Markov nasumični proces u kojem su prelazi iz države E dozvoljena samo u susjednim stanjima e ja - 1, e i i i + 1. Proces uzgoja i smrti je adekvatan model za opisivanje promjena koje se događaju u količini biološkog stanovništva. Nakon ovog modela, kaže se da je proces u državi i ja, ako je obim stanovništva jednak članovima. U ovom slučaju, tranzicija iz države i I ja i + 1 odgovara rođenju, a prijelaz iz i i I-1 - smrt, pretpostavlja se da količina stanovništva može varirati ne više od jedan; To znači da višestruki istovremeno rođeni i / ili smrt nije dozvoljen za uzgoj procesa i smrti.
Diskretni reproduktivni procesi i smrt su manje zanimljivi od kontinuiranih, tako da se u budućnosti ne smatraju detaljno i fokusiraju se na kontinuirane procese. Međutim, treba napomenuti da gotovo paralelni izračuni prelaze za diskretne procese. Prijelaz procesa reprodukcije i smrti iz države i vraćam se na stanje e ja predstavljam neposredno interesovanje samo za diskretne lance Markov; U kontinuiranom slučaju, intenzitet kojim se proces vraća u trenutno stanje jednak je beskonačnoj beskonačnosti, a ova beskonačnost je isključena i definirana je na sljedeći način:
U slučaju procesa reprodukcije i smrti s diskretnim vremenom vjerojatnosti prijelaza između država

Ovdje je vjerovatnost da će u sljedećem koraku (u smislu biološkog stanovništva) postojala jedna smrt koja smanjuje količinu stanovništva prije nego što je volumen stanovništva jednak ovom koraku. Slično tome, B ja sam vjerojatnost rođenja u sljedećem koraku koji vodi do povećanja obima populacije u; Vjerojatnost je da se nijedan od tih događaja neće dogoditi i u sljedećem koraku se količina stanovništva neće promijeniti. Dozvoljene su samo ove tri mogućnosti. Jasno je da, jer smrt ne može doći, ako neka vrsta umiranja.
Međutim, u protutežnom intuiciji je dopušteno da, što odgovara mogućnošću rođenja, kada u populaciji nije niti jedan član. Iako se to može smatrati spontanim rođenjem ili božanskom kreiranjem, ali u teoriji diskretnih sustava takav je model potpuno smislena pretpostavka. Naime, model je takav: Stanovništvo je protok potraživanja u sistemu, smrt znači brigu o zahtjevu sistema, a rođenje odgovara novoj potražnji sustavu. Jasno je da je u takvom modelu sasvim moguće ući u novi zahtjev (rođen) u slobodnom sistemu. Matrica verovatnoće prelaska za opšti proces uzgoja i smrti ima sledeći obrazac:

Ako je Markov lanac konačan, tada je posljednja linija matrice napisana u obliku; To odgovara činjenici da nije dozvoljena reprodukcija nakon što stanovništvo dostigne maksimalni volumen n. Matrica T sadrži nulte članove samo na glavnoj dijagonalnoj i dva dijagonala najbliže njemu. Zbog takve određene vrste matrice t, prirodno je očekivati \u200b\u200bda analiza procesa uzgoja i smrti ne bi trebalo uzrokovati poteškoće. Zatim ćemo razmotriti samo kontinuirane procese reprodukcije i smrti, u kojim su prelazima iz države e mogući samo u susjednim državama i i-1 (smrt) i i i + 1 (rođenje). Označite ja intenzitet reprodukcije; Opisuje brzinu s kojom se pojavljuje reprodukcija u količini i populaciji. Slično tome, kroz I, označavamo intenzitet smrti, specificirajući brzinu s kojom se smrt javlja u količini jačine I. Imajte na umu da uvedeni intenzitet uzgoja i smrt ne ovise o vremenu i ovise o državi E ja, dakle, dobivamo kontinuirani homogen lanac Markovskog uzgoja i smrti. Ove posebne oznake uvode se jer direktno dovode do notacije usvojene u teoriji diskretnih sistema. Ovisno o prethodno unesenim oznakama, imamo:
i \u003d q i, i + 1 i i \u003d q i, i-1.
Zahtjev za prihvatljive prijelaze samo u najbližim susjednim državama znači da se na osnovu činjenice
dobijamo Q II \u003d - (i + i). Dakle, matrica intenziteta prijelaza općeg homogenog procesa uzgoja i smrti uzima oblik:

Imajte na umu da s izuzetkom glavne dijagonale i njenog susjednog i odozgo, svi su elementi matrice nula. Odgovarajući grafikon intenziteta tranzicije predstavljen je na odgovarajućoj slici (2.1):
Slika 2.1 - Broj intenziteta tranzicije za proces uzgoja i smrti
Preciznija određivanje kontinuiranog procesa uzgoja i smrti je sljedeći: Neki proces je proces uzgoja i smrti, ako je to homogeni lanac Markov sa mnogim državama (E 0, E 1, E 2, ... ), ako su rođenje i smrt neovisni događaji (ovo slijedi direktno iz imovine Markov) i ako su zadovoljni sljedeći uvjeti:
(tačno 1 rođenje u vremenskom intervalu (T, T + DT), zapremina stanovništva je jednak I);
(tačno 1 smrt u vremenskom intervalu (T, T + DT) | Zapremina populacije jednak je I);
\u003d (tačno 0 rođenja u vremenskom intervalu (T, T + DT) | Količina stanovništva je jednaka I);
\u003d (tačno 0 smrtnih slučajeva u vremenskom intervalu (T, T + DT) | Količina stanovništva je jednaka I).
Stoga ,? t tačnost da postoji vjerovatnoća rođenja novog pojedinca u populaciji N pojedinca, a vjerojatnost smrti pojedinaca u ovom stanovništvu tokom vremena.
Verovatnoće tranzicije zadovoljavaju suprotne jednadžbe Kolmogorova. Stoga je verovatnoća da je kontinuirani proces reprodukcije i smrti u vremenu t u stanju i (svezak stanovništvu jednak I) određuje se u obrascu (2.1):

Da bi se riješio dobijeni sustav diferencijalnih jednadžbi u zastupljenom slučaju, kada su vjerojatnosti PI (T), i \u003d 0,1,2, ..., ovise o vremenu, potrebno je odrediti distribuciju početnih vjerojatnosti PI (0), i \u003d 0,1,2, ..., na t \u003d 0. Pored toga, stanje normalizacije treba biti zadovoljeno.
Sada smatramo najjednostavniji proces čiste reprodukcije, koji je definiran kao proces za koji sam i \u003d 0 za sve I. Pored toga, za još veće pojednostavljenje problema, pretpostavimo da sam i \u003d za sve i \u003d 0,1,2, .... Zamjena ovih vrijednosti u jednadžbi (2.1) dobivamo (2.2):

Za jednostavnost pretpostavljamo da proces započinje u nulti trenutku na nula članova, odnosno:
Odavde za P 0 (T) Dobivamo rješenje:
Zamjena ovog rješenja na jednadžbu (2.2) na I \u003d 1 stižemo u jednadžbu:
Otopina ove diferencijalne jednake očito ima obrazac:
Ovo je poznata raspodjela Poissona. Dakle, proces čiste reprodukcije stalnim intenzitetom dovodi do niza rođenja koji formiraju poissonski protok.
Najveće interesovanje za praktične izraze predstavljaju vjerojatnosti stanja uzgoja i smrti u stalnom režimu. Pod pretpostavkom da proces ima ergodic nekretninu, odnosno postoje ograničenja
okrećemo se na definiciju graničnih vjerojatnosti p i. Jednadžbe za određivanje vjerojatnosti stacionarnog režima mogu se dobiti izravno od (2.1), s obzirom na to da DP I (t) / DT \u003d 0 sa:
Rezultirajući sustav jednadžbi rješava se u pogledu stanja normalizacije (2.4):
Sistem jednadžbi (2.3) za utvrđeni način procesa reprodukcije i smrti može se izravno izvršiti grafikom intenziteta prijelaza na slici 2.1, primjenjujući princip jednakosti vjerojatnosti u zasebnom stanju procesa. Na primjer, ako smatrate da ste u stalnom režimu, tada:
intenzitet toka vjerojatnosti u i
intenzitet protoka verovatnoće od.
U ravnotežnom stanju ta dva toka moraju biti jednaka, pa se samim tim dobijamo direktno:
Ali to je upravo prva jednakost u sistemu (2.3). Slično tome, možete dobiti drugu ravnopravnost sistema. Isti obrazloženje o očuvanju protoka, koje je prethodno prikazano, može se primijeniti na tok vjerojatnosti kroz bilo koju zatvorenu obrub. Na primjer, umjesto da istakne svako stanje i napravite jednadžbu za njega, možete odabrati niz kontura, prvo pokriva državu E 0, drugi je država E 0 i E 1, uključujući i 1, uključujući i 1, uključujući i 1, uključujući Sljedeća država svaki put u novoj granici. Zatim za I-TH Contour (surroundment e 0, E 1, ..., E I-1), očuvanje protoka vjerojatnosti može se napisati u sljedećem jednostavnom obliku:
Jednakost (2.5) može se formulisati u pravilu: Za najjednostavniji sistem reprodukcije i smrti u bolničkom režimu, važni su potoci između bilo koje dvije susjedne države jednake.
Rezultirajući sustav jednadžbi ekvivalentan je smanjenim ranijim. Za sastavljanje posljednjeg sistema jednadžbi potrebno je izvršiti vertikalnu liniju koja odvaja susjedne države i izjednačavaju struju kroz rezultirajuću granicu.
Rješenje sistema (2.5) može se naći matematičkom indukcijom.
U i \u003d 1 imamo
Vrsta dobijenog jednakosti pokazuje da je ukupno rješenje sustava jednadžbi (2.5) obrazac:
ili, s obzirom na to, po definiciji, rad na praznom setu je jedan:
Stoga su sve vjerojatnosti p i za stalni režim izraženi samo putem jedinog nepoznatog konstante P 0. Ravnopravnost (2.4) daje dodatno stanje za određivanje P 0. Zatim, zbrojevši sve ja, za p 0 dobivamo (2.7):

Okrenimo se na pitanje postojanja stacionarne vjerojatnosti p i. Da bi se izrazi navedeni vjerovatno, uslov se obično naziva tako da je P 0\u003e 0. To očigledno nameće ograničenje koeficijenata reprodukcije i smrt u odgovarajućim jednadžbama. U osnovi je potrebno da sustav ponekad bude prazan; Ova stabilnost čini se vrlo razumnim ako se okrenete primjerima stvarnog života. Ako prebrzo raste u usporedbi, može se pokazati da će sa pozitivnom verovatnoćom na kraju vremena T, proces napustiti fazni prostor (0,1, ...) u "beskonačno udaljenom poanta?" (Pojedinci u populaciji bit će previše). Drugim riječima, proces neće biti redovan, a zatim će jednakost (2.4) biti prekinuta. Definiramo sljedeće dvije količine:

Za regularnost procesa reprodukcije i smrti potrebno je i dovoljno za S 2 \u003d.
Za postojanje svoje stacionarne distribucije potrebno je i dovoljno za 1< .
Da bi se sve države e I I procesa postupka u pitanju i smrti bile ergodiće, te dovoljna konvergencija serije S 1< , при этом ряд должен расходиться S 2 = . Только эргодический случай приводит к установившимся вероятностям P i , i = 0, 1, 2, …, и именно этот случай представляет интерес. Заметим, что условия эргодичности выполняются, например, когда, начиная с некоторого i, все члены последовательности {} ограничены единицей, т. е. тогда, когда существует некоторое i 0 (и некоторое С<1) такое, что для всех ii 0 выполняется неравенство:
Ova nejednakost može se dati jednostavno tumačenje: počevši od neke države i i za sve naredne države, intenzitet potoka reprodukcije mora biti manji od intenziteta protoka smrti.
Ponekad u praksi postoje procesi "čiste" reprodukcije. Proces "čiste" reprodukcije je takav proces smrti i reprodukcije, u kojem su intenzitet svih smrtnih tokova nula. Grafikon država takvog procesa bez ograničavanja broja država prikazan je na slici (2.2):

Slika 2.2 - grafikon intenziteta tranzicije za proces "čiste" reprodukcije
Slično tome, uvodi se koncept "čiste" smrti. Proces "čiste" smrti naziva se takav proces smrti i reprodukcije, u kojem su intenzitet svih reprodukcijskih tokova nula. Grafikon država takvog procesa bez ograničavanja broja država prikazan je na slici:

Slika 2.3 - Broj intenziteta tranzicije za proces "čiste" smrti
Kolmogorov sistem jednadžbi za takve procese može se dobiti iz sistema jednadžbi (2.1) u kojem je potrebno staviti sve intenzitet protočnog procesa teče jednake nuli :.
Najjednostavnija generalizacija Poissonovog procesa dobiva se pod pretpostavkom da vjerojatnosti skokova mogu ovisiti o trenutnoj stanju sustava. To nas vodi na sledeće zahteve.
Postulati. (i) Direktan prijelaz iz države moguće je samo državi. (ii) ako je sistem u trenutku u stanju, zatim (uslovno) vjerojatnost jednog skoka u narednom kratkog vremenskog intervala između i jeste Tada je (uslovno) vjerojatnost više od jednog skoka u ovom intervalu.
Izrazito obilježje ove pretpostavke je da vrijeme koje sistem provodi u bilo kojem određenom stanju ne igra nikakvu ulogu; Moguće su iznenadne promjene države, međutim, dok je sustav u jednoj državi, ne stare.
Neka je vjerovatno da je u trenutku vremena sustav u stanju. Ove funkcije zadovoljavaju sistem diferencijalnih jednadžbi, koji se mogu izvesti pomoću razloga prethodnog stavka sa samo promjenom koja (5) u prethodnom stavku zamjenjuju
Dakle, dobivamo glavni sistem diferencijalnih jednadžbi
 (2)
(2)
U Poissonovom procesu bilo je prirodno pretpostaviti da u trenutku vremena 0, sustav izlazi iz početnog stanja. Sada možemo priznati općenitiji slučaj kada sistem izlazi iz proizvoljnog početnog stanja. Onda to shvatamo
Ovi početni uvjeti pojedinačni definiraju rješenje sustava (2). (Posebno,). Izričito formule za nezavisno prikazane od strane mnogih autora, ali za nas ne predstavljaju interes.
Primjer. Radioaktivni propadanje. Kao rezultat emisije čestica ili - radijusa, radioaktivnog atoma, kažu uranijum, može pretvoriti u atom druge vrste. Svaki pogled je moguće stanje, a kada se proces nastavlja, dobijamo niz prijelaza. Prema usvojenim fizičkim teorijama, verovatnoća tranzicije ostaje nepromijenjena sve dok atom ne bude u stanju, a ova hipoteza pronalazi izraz u našoj početnoj pretpostavci. Stoga je ovaj proces opisan diferencijalnim jednadžbama (2) (činjenica, poznati fizičari). Ako je - konačno stanje, iz koje nijedna druga prijelaza ne mogu biti nemoguća, tada je sistem (2) na razbijen. (Kad automatski dobijemo).
Ministarstvo prosvete Republike Bjelorusije
Osnivanje obrazovanja
"Državni univerzitet Gomel
nazvan po Francisu Skorini "
Matematički fakultet
Odjel za ekonomsku teoriju kibernetike i vjerojatnosti
Projekt predmeta
Stacionarne karakteristike procesa uzgoja i smrti
Izvršitelj:
Bukhovets Victoria
Alexandrovna
Naučni savetnik:
Šef odjela,
Malinkovsky Yuri.
Vladimirovich
Gomel 2011.
Uvođenje
Procesi uzgoja i smrti
Primjeri uzgoja i smrtnih procesa u slučaju jednostavnih sistema za održavanje masovnih održavanja
3 Definicija matematičkog očekivanja za sistem za održavanje masovnog održavanja m / m / n
4 Definicija matematičkog očekivanja za sistem za održavanje masovnog održavanja m / m / n / n
Definicija matematičkog očekivanja za neke procese uzgoja i smrti
2 Proces uzgoja i smrti s linearno rastućim intenzitetom rođenja i kvadratno rastući intenzitet smrti
4 Dodatni protok i beskonačni broj instrumenata
5 Sistem sa ograničenjem za vreme boravka aplikacije
6 Sistem sa ograničenjem za vrijeme boravka aplikacije, dodatni potok i beskonačan broj instrumenata
Zaključak
masovno održavanje matematičkog očekivanja
Uvođenje
U ovom radu, shema kontinuiranih Markovskog lanca razmatrat će se - takozvani "dijagram smrti i reprodukcije"
Proces reprodukcije i smrti je slučajni proces sa brojevima (konačnim ili beskonačnim) setom država koji teče u diskretnom ili neprekidnom vremenu. To je da neki sistem nasumičnim trenucima vremena prolazi iz jedne države u drugu, a prelazi između država nastaju sa skokom kada se događaju neki događaji. U pravilu su ovi događaji dvije vrste: jedan od njih uvjetno se naziva rođenje nekih predmeta, a druga je smrt ovog objekta.
Ova je tema izuzetno relevantna zbog velike važnosti Markovskog procesa u istraživanju ekonomskih, ekoloških i bioloških procesa, osim Markovskog procesa na srcu teorije masovne usluge, koji se trenutno aktivno koristi u različitim ekonomskim područjima, uključujući upravljanje procesima u preduzeću.
Markov procesi smrti i reprodukcije široko se koriste u objašnjavanju različitih procesa koji se javljaju u fizici, biosferi, ekosustavu itd. Treba napomenuti da je ova vrsta Markov procesa precizno primila svoje ime zbog široko rasprostranjene upotrebe u biologiji, posebno kada modeliranje smrti i reprodukcije pojedinca raznih populacija.
Ovaj rad će biti zadatak, čija je svrha definirati matematička očekivanja za neke procese uzgoja i smrti. Primjeri proračuna prosječnog broja prijava u sustavu u stacionarnom režimu i procjene vrše se za različite slučajeve uzgoja i procesa smrti.
1. Procesi uzgoja i smrti
Procesi reprodukcije i smrti posebni su slučaj Markov slučajnih procesa, koji se, ipak, vrlo široko koriste u proučavanju diskretnih sistema sa stohastičnom prirodom funkcioniranja. Proces reprodukcije i smrti je Markov nasumični proces u kojem prelazi iz države e i. Dozvoljeno samo u susjednim državama e i-1. E. i. i E. i + 1. . Proces uzgoja i smrti je adekvatan model za opisivanje promjena koje se događaju u količini biološkog stanovništva. Nakon ovog modela kažu da je proces u državi e i. Ako je volumen stanovništva jednak članovima. U ovom slučaju, tranzicija iz države E i. Da se navodi E. i + 1. odgovara rođenju i prelazu iz e i. u E. i-1. - Smrt, pretpostavlja se da se količina stanovništva može varirati ne više od jednog; To znači da višestruki istovremeno rođeni i / ili smrt nije dozvoljen za uzgoj procesa i smrti.
Diskretni reproduktivni procesi i smrt su manje zanimljivi od kontinuiranih, tako da se u budućnosti ne smatraju detaljno i fokusiraju se na kontinuirane procese. Međutim, treba napomenuti da gotovo paralelni izračuni prelaze za diskretne procese. Tranzicijski proces uzgoja i smrti iz države E i. natrag na državu e i. Predstavlja direktan interes samo za diskretne lance Markov; U kontinuiranom slučaju, intenzitet kojim se proces vraća u trenutno stanje jednak je beskonačnoj beskonačnosti, a ova beskonačnost je isključena i definirana je na sljedeći način:
U slučaju procesa reprodukcije i smrti s diskretnim vremenom vjerojatnosti prijelaza između država
Ovdje je Vjerovatnost da će u sljedećem koraku (u smislu biološkog stanovništva) postojati jedna smrt koja smanjuje količinu stanovništva, pre nego što je volumen stanovništva jednak ovom koraku. Slično tome, BI je vjerojatnost rođenja u sljedećem koraku, što dovodi do povećanja količine stanovništva u; Vjerojatnost je da se nijedan od tih događaja neće dogoditi i u sljedećem koraku se količina stanovništva neće promijeniti. Dozvoljene su samo ove tri mogućnosti. Jasno je da, jer smrt ne može doći, ako neka vrsta umiranja.
Međutim, u protutežnom intuiciji je dopušteno da, što odgovara mogućnošću rođenja, kada u populaciji nije niti jedan član. Iako se to može smatrati spontanim rođenjem ili božanskom kreiranjem, ali u teoriji diskretnih sustava takav je model potpuno smislena pretpostavka. Naime, model je takav: Stanovništvo je protok potraživanja u sistemu, smrt znači brigu o zahtjevu sistema, a rođenje odgovara novoj potražnji sustavu. Jasno je da je u takvom modelu sasvim moguće ući u novi zahtjev (rođen) u slobodnom sistemu. Matrica verovatnoće prelaska za opšti proces uzgoja i smrti ima sledeći obrazac:
Ako je Markov lanac konačan, tada je posljednja linija matrice napisana u obliku; To odgovara činjenici da nije dozvoljena reprodukcija nakon što stanovništvo dostigne maksimalni volumen n. Matrica T sadrži nulte članove samo na glavnoj dijagonalnoj i dva dijagonala najbliže njemu. Zbog takve određene vrste matrice t, prirodno je očekivati \u200b\u200bda analiza procesa uzgoja i smrti ne bi trebalo uzrokovati poteškoće. Zatim ćemo razmotriti samo kontinuirane procese reprodukcije i smrti, u kojim su prelazima iz EI stanja moguća samo u susjednim državama EI-1 (smrt) i EI + 1 (rođenje). Označavaju li intenzitet reprodukcije; Opisuje brzinu s kojom se pojavljuje reprodukcija u količini i populaciji. Slično tome, kroz MI, označavamo intenzitet smrti, specificirajući brzinu s kojom se smrt javlja u količini jačine I. Imajte na umu da uvedeni uzgojni intenzitet i smrt ne ovise o vremenu i ovise o državi EI, stoga dobijamo kontinuirani homogen lanac Markovskog uzgoja i smrti. Ove posebne oznake uvode se jer direktno dovode do notacije usvojene u teoriji diskretnih sistema. Ovisno o prethodno unesenim oznakama, imamo:
li \u003d qi, i + 1 i mi \u003d qi, i-1.
Zahtjev za prihvatljive prijelaze samo u najbližim susjednim državama znači da se na osnovu činjenice
dobijamo Qii \u003d - (MI + LI). Dakle, matrica intenziteta prijelaza općeg homogenog procesa uzgoja i smrti uzima oblik:
Imajte na umu da s izuzetkom glavne dijagonale i njenog susjednog i odozgo, svi su elementi matrice nula. Odgovarajući grafikon intenziteta tranzicije predstavljen je na odgovarajućoj slici (2.1):
Slika 2.1 - Broj intenziteta tranzicije za proces uzgoja i smrti
Precizniji određivanje kontinuiranog procesa uzgoja i smrti je sljedeći: neki proces je proces uzgoja i smrti, ako je to homogeni lanac Markov sa više država (E0, E1, E2, ...), ako Rođenje i smrt su neovisni događaji (slijedi direktno iz imovine Markov) i ako su sigurni uslovi zadovoljni:
1) (tačno 1 rođenje u vremenskom intervalu (T, T +? T), zapremina stanovništva je jednak I);
2) (tačno 1 smrt u vremenskom intervalu (T, T +? T) | Količina stanovništva je jednaka I);
3) \u003d (tačno 0 rođenja u vremenskom intervalu (T, T +? T) | Količina stanovništva je jednaka I);
4) \u003d (tačno 0 smrtnih slučajeva u vremenskom intervalu (T, T +? T) | Količina stanovništva je jednaka I).
Stoga ,? t tačnost da postoji vjerovatnoća rođenja novog pojedinca u populaciji N pojedinca, a vjerojatnost smrti pojedinaca u ovom stanovništvu tokom vremena.
Verovatnoće tranzicije zadovoljavaju suprotne jednadžbe Kolmogorova. Dakle, vjerojatnost da je kontinuirani proces reprodukcije i smrti u vrijeme T u državi EI (obim stanovništva je jednak I) određuje se u obrascu (2.1):
Da bi se rešio rezultirajuće sustav diferencijalnih jednadžbi u zaintalationalnom slučaju, kada su vjerojatnosti PI (T), i \u003d 0,1,2, ..., ovise o vremenu, potrebno je postaviti distribuciju početnih vjerojatnih vjerojatnosti PI (0), i \u003d 0,1,2, ..., na t \u003d 0. Pored toga, stanje normalizacije treba biti zadovoljeno.
Razmotrite sada najjednostavniji proces čiste reprodukcije, koji je definiran kao proces za koji mi \u003d 0 za sve I. Pored toga, za još veće pojednostavljenje problema, pretpostavimo da li \u003d l za sve i \u003d 0,1,2, .... Zamjena ovih vrijednosti u jednadžbi (2.1) dobivamo (2.2):
Za jednostavnost pretpostavljamo da proces započinje u nulti trenutku na nula članova, odnosno:
Dakle, za P0 (T) Dobili smo rješenje:
Zamjena ovog rješenja na jednadžbu (2.2) na I \u003d 1 stižemo u jednadžbu:
Otopina ove diferencijalne jednake očito ima obrazac:
Ovo je poznata raspodjela Poissona. Dakle, proces čiste reprodukcije stalnim intenzitetom ja vodi do niza rođenja koji formiraju poissonski protok.
Najveće interesovanje za praktične izraze predstavljaju vjerojatnosti stanja uzgoja i smrti u stalnom režimu. Pod pretpostavkom da proces ima ergodic nekretninu, odnosno postoje ograničenja
okrenite se definiciji graničnih vjerojatnosti PI. Jednadžbe za određivanje vjerojatnosti stacionarnog načina mogu se dobiti izravno od (2.1), s obzirom na taj DPI (t) / dt \u003d 0 sa:
Rezultirajući sustav jednadžbi rješava se u pogledu stanja normalizacije (2.4):
Sistem jednadžbi (2.3) za utvrđeni način procesa reprodukcije i smrti može se izravno izvršiti grafikom intenziteta prijelaza na slici 2.1, primjenjujući princip jednakosti vjerojatnosti u zasebnom stanju procesa. Na primjer, ako smatrate da je status EI u stalnom režimu:
intenzitet toka vjerojatnosti u i
intenzitet protoka verovatnoće od.
U ravnotežnom stanju ta dva toka moraju biti jednaka, pa se samim tim dobijamo direktno:
Ali to je upravo prva jednakost u sistemu (2.3). Slično tome, možete dobiti drugu ravnopravnost sistema. Isti obrazloženje o očuvanju protoka, koje je prethodno prikazano, može se primijeniti na tok vjerojatnosti kroz bilo koju zatvorenu obrub. Na primjer, umjesto da razlikuje svako stanje i izvršite jednadžbu za njega, možete odabrati niz kontura, prvo pokriva državu E0, drugu državu E0 i E1, i tako dalje, uključujući svaki put kada je sljedeća država još jedna država. Zatim za I-TH Contour (surround e0, E1, ..., EI-1), tok vjerojatnosti može se napisati u sljedećem jednostavnom obliku:
Jednakost (2.5) može se formulisati u pravilu: Za najjednostavniji sistem reprodukcije i smrti u bolničkom režimu, važni su potoci između bilo koje dvije susjedne države jednake.
Rezultirajući sustav jednadžbi ekvivalentan je smanjenim ranijim. Za sastavljanje posljednjeg sistema jednadžbi potrebno je izvršiti vertikalnu liniju koja odvaja susjedne države i izjednačavaju struju kroz rezultirajuću granicu.
Rješenje sistema (2.5) može se naći matematičkom indukcijom.
U i \u003d 1 imamo
Vrsta dobijenog jednakosti pokazuje da je ukupno rješenje sustava jednadžbi (2.5) obrazac:
ili, s obzirom na to, po definiciji, rad na praznom setu je jedan:
Dakle, sve vjerojatnosti PI za stalni način izražene su samo samo nepoznatom konstantom P0. Ravnopravnost (2.4) daje dodatno stanje koje vam omogućava da odredite P0. Zatim, sažetim na sve ja, za P0 koji dobijamo (2,7):
Okrenimo se na pitanje postojanja stacionarne vjerojatnosti PI. Da bi se izrazi dobiveni za definiranje vjerojatnosti, zahtjev se obično naziva P0\u003e 0. To očigledno nameće ograničenje koeficijenata reprodukcije i smrt u odgovarajućim jednadžbama. U osnovi je potrebno da sustav ponekad bude prazan; Ova stabilnost čini se vrlo razumnim ako se okrenete primjerima stvarnog života. Ako prebrzo raste u usporedbi, može se pokazati da će sa pozitivnom verovatnoćom na kraju vremena T, proces napustiti fazni prostor (0,1, ...) u "beskonačno udaljenom poanta?" (Pojedinci u populaciji bit će previše). Drugim riječima, proces neće biti redovan, a zatim će jednakost (2.4) biti prekinuta. Definiramo sljedeće dvije količine:
Za pravilnost procesa reprodukcije i smrti, potrebno je i dovoljno za S2 \u003d.
Za postojanje svoje stacionarne distribucije potrebno je i dovoljno za S1< .
Da bi se sve države EI procesa reprodukcije i smrti razmatrale, potrebno je i dovoljno za konvergenciju serije S1< , при этом ряд должен расходиться S2 = . Только эргодический случай приводит к установившимся вероятностям Pi, i = 0, 1, 2, …, и именно этот случай представляет интерес. Заметим, что условия эргодичности выполняются, например, когда, начиная с некоторого i, все члены последовательности {} ограничены единицей, т. е. тогда, когда существует некоторое i0 (и некоторое С<1) такое, что для всех ii0 выполняется неравенство:
Ova nejednakost može se dati jednostavna interpretacija: počevši od neke države EI i za sve naredne države, intenzitet potoka reprodukcije mora biti manji od intenziteta protoka smrti.
Ponekad u praksi postoje procesi "čiste" reprodukcije. Proces "čiste" reprodukcije je takav proces smrti i reprodukcije, u kojem su intenzitet svih smrtnih tokova nula. Grafikon država takvog procesa bez ograničavanja broja država prikazan je na slici (2.2):
Slika 2.2 - grafikon intenziteta tranzicije za proces "čiste" reprodukcije
Slično tome, uvodi se koncept "čiste" smrti. Proces "čiste" smrti naziva se takav proces smrti i reprodukcije, u kojem su intenzitet svih reprodukcijskih tokova nula. Grafikon država takvog procesa bez ograničavanja broja država prikazan je na slici:
Slika 2.3 - Broj intenziteta tranzicije za proces "čiste" smrti
Kolmogorov sistem jednadžbi za takve procese može se dobiti iz sistema jednadžbi (2.1) u kojem je potrebno staviti sve intenzitet protočnog procesa teče jednake nuli :.
2. Primjeri oštećenja smrti u slučaju jednostavnih sistema za održavanje masovnih održavanja
1 Definicija matematičkog očekivanja za sistem za održavanje masovnog održavanja m / m / 1
Sistem masovnog održavanja koji se razmatra proces reprodukcije i smrti sa sljedećim grafom tranzicije (slika 3.1):
Slika 3.1 - Grovni intenzitet tranzicije za sistem M / M / 1
Od stanja ergodišnja za proces smrti i reprodukcije, slijedi da ako postoji jedna nepomična distribucija koja se podudara s ergodilom naziva se omjer mrežnog opterećenja. Ravnotežna jednadžba ima oblik u kojem ćemo to pronaći:
Vjerovatnoća se može naći korištenjem stanja normalizacije (2.4), odakle slijedi to i samim tim
i.E. Broj prijava u takvom sistemu masovnog održavanja u stacionarnom režimu ima geometrijsku distribuciju.
Jednostavno pronalazak produktivne funkcije ove distribucije:
Odavde dobijamo izraz za prosječni broj aplikacija u sistemu u stacionarnom režimu:
Očito, red u masovnom sustavu raste neograničen.
2 Definicija matematičkog očekivanja za sistem za održavanje masovnog održavanja m / m / n / 0
Ovo je sistem za gubitak bez čekanja. Ako aplikacija uđe u sistem u vrijeme kada je usluga zauzeta svim n linijama, izgubi se. Takav sistem je uveo danskog inženjera Erlang početkom prošlog vijeka i primijenjen je kao model obrade poziva koji unose telefonsku razmjenu. Grafikon prijelaza za takav sistem za održavanje masovnog održavanja ima obrazac (slika 3.2):
Slika 3.2 - Intenziti intenziteta brojanja za M / M / N / 0 sistem
Budući da je broj stanja sustava, a Markov lanac je nepovratan, jedina stacionarna distribucija koja se podudara s ergodiškom, uvijek postoji s bilo kojim parametrima.
Odavde imamo:
Verovatnoća, kao i uvek, može se naći iz uvjeti normalizacije (2.4), lokacija:
Tako imamo:
Prosječni broj aplikacija u sustavu određuje se odnosom:
Sa velikim n, možete koristiti asimptotiku.
2.3 Definicija matematičkog očekivanja za sistem za održavanje masovnog održavanja m / m / n
Ovo je višebolni sistem sa očekivanjem. Ako su sve n linije zauzeti servisnim aplikacijama, tada je intenzitet usluge jednak. Grafikon tranzicije za ovaj sistem ima pogled (slika 3.3):
Slika 3.3 - Brojite intenzitet prelaza za M / M / N sistem
Stacionarna distribucija postoji ako
Jednadžbe ravnoteže su sljedeće:
gde, slično prethodnom slučaju, dohvati
Uvjeti normalizacije u ovom slučaju poduzet će obrazac:
odakle to slijedi
Prosječan broj aplikacija u bolničkom režimu je jednak
2.4 Definicija matematičkog očekivanja za sistem za održavanje masovnog održavanja m / m / n / n
Ovo je višestrani sistem sa ograničenim brojem mjesta. Razlikuje se od prethodnog sistema masovnog održavanja činjenicom da u njemu postoje samo n mjesta. Stoga grafikon prijelaza u ovom slučaju ima obrazac (slika 3.4):
Slika 3.4 - Brojite intenzitet prelaza za M / M / N / N sistem
Budući da je broj stanja sustava, naravno, jedina stacionarna distribucija uvijek postoji s bilo kojim parametrima. Ravnotežne jednadžbe uzimaju obrazac:
Tamo gdje slijedi tu bolničke vjerojatnosti, imaju isti oblik kao i za prethodni sistem masovnog sustava, sa jeme razlikama za koju su definirani. Na ovaj način
Verovatnoća se utvrđuje iz uvjeti normalizacije (2.4):
odakle ti:
Prosječni broj aplikacija u sustavu određuje se odnosom:
3. Definicija matematičkog očekivanja za neke procese uzgoja i smrti
1 proces uzgoja i smrti sa linearno rastućim intenzitetom rođenja i smrti
Slika 1 - Grafikon intenziteta tranzicije za prvi slučaj procesa uzgoja i smrti
Napišemo jednadžbe ravnotežom za stacionarne vjerojatnosti država:
Da bismo odredili matematičko očekivanje, koristimo sljedeću formulu:
gde se određuje formulom.
Dakle, prosječni broj aplikacija u sistemu u fiksnom režimu je:
3.2 Proces uzgoja i smrti sa linearno rastućim intenzitetom rođenja i kvadratno rastući intenzitet smrti
Neka brzina LI, sa kojom reprodukcija u populaciji glasnoće i intenziteta smrti MI, specificirajući brzinu na kojoj se smrt javlja u količini I i stanovništva, određeni su sljedećim pravilom:
Grafikon intenziteta tranzicije za ovaj proces uzgoja i smrti ima oblik:
Slika 2 - Grafikon tranzicijskih intenziteta za drugi slučaj procesa uzgoja i smrti
Napišemo jednadžbe ravnotežom za stacionarne vjerojatnosti država:
3 Proces uzgoja i smrti sa linearno rastućim intenzitetom rođenja i kvadratno rastući intenzitet smrti
Neka brzina LI, sa kojom reprodukcija u populaciji glasnoće i intenziteta smrti MI, specificirajući brzinu na kojoj se smrt javlja u količini I i stanovništva, određeni su sljedećim pravilom:
Grafikon tranzicijskih intenziteta za ovaj proces uzgoja i smrti ima oblik
Slika 3 - Broj intenziteta tranzicije za treći slučaj procesa uzgoja i smrti
Napišemo jednadžbe ravnotežom za stacionarne vjerojatnosti država:
Da bismo pronašli matematičko očekivanje, koristimo formulu. Dobijamo da je prosječni broj prijava u stacionarnom režimu:
3.4 Dodatni tok i beskonačni broj instrumenata
Neka brzina LI, sa kojom reprodukcija u populaciji glasnoće i intenziteta smrti MI, specificirajući brzinu na kojoj se smrt javlja u količini I i stanovništva, određeni su sljedećim pravilom:
Grafikon intenziteta tranzicije za ovaj proces uzgoja i smrti ima oblik:
Slika 4 - grafikon intenziteta tranzicije za četvrti slučaj procesa uzgoja i smrti
Napišemo jednadžbe ravnotežom za stacionarne vjerojatnosti država:
Da bismo pronašli matematičko očekivanje, koristimo formulu. Dobijamo da je prosječni broj prijava u stacionarnom režimu:
Napravite procjenu odozgo:
na ovaj način:
3.5 Sistem sa ograničenjem za vrijeme boravka aplikacije
Neka brzina LI, sa kojom reprodukcija u populaciji glasnoće i intenziteta smrti MI, specificirajući brzinu na kojoj se smrt javlja u količini I i stanovništva, određeni su sljedećim pravilom:
Grafikon intenziteta tranzicije za ovaj proces uzgoja i smrti ima oblik:
Slika 5 - Grafikon intenziteta tranzicije za peti slučaj procesa uzgoja i smrti
Napišemo jednadžbe ravnotežom za stacionarne vjerojatnosti država:
Da bismo pronašli matematičko očekivanje, koristimo formulu. Dobijamo da je prosječni broj prijava u stacionarnom režimu:
Napravite procjenu odozgo:
na ovaj način:
Dobijamo sljedeću ocjenu za prosječni broj aplikacija u sistemu u stacionarnom režimu:
3.6 Sistem sa ograničenjem za vreme boravka aplikacije, dodatni stream i beskonačni broj instrumenata
Neka brzina, s kojom se širenje glasnoće I stanovništva i intenzitet smrti MI, specificirajuća brzina s kojom se navodi smrt u populaciji glasnoće, odlučuju se u pravilu predavanja:
Grafikon intenziteta tranzicije za ovaj proces uzgoja i smrti ima oblik:
Slika 6 - Broj intenziteta tranzicije za šesti slučaj procesa uzgoja i smrti
Napišemo jednadžbe ravnotežom za stacionarne vjerojatnosti država:
Da bismo pronašli matematičko očekivanje, koristimo formulu. Dobijamo da je prosječni broj prijava u stacionarnom režimu:
Napravite procjenu odozgo:
na ovaj način:
Dobijamo sljedeću ocjenu za prosječni broj aplikacija u sistemu u stacionarnom režimu:
Zaključak
Dakle, pogledali smo suštinu i matematički model procesa uzgoja i smrti i na njenu osnovu - modeli četiri osnovne vrste sustava masovnih usluga: sa gubicima i očekivanjima. Utvrdio da se Markov proces uzgoja i smrti sa neprekidnim vremenom naziva takav slučajni proces koji može poduzeti onoliko negativnih vrijednosti; Od čijih promjena mogu se pojaviti u bilo kojem trenutku t, dok u bilo kojem trenutku može ili povećati jedan ili smanjiti jedan ili ostati nepromijenjen.
Također u ovom radu predstavljeni su teorijski certifikat i primjeri utvrđivanja matematičkih očekivanja za različite procese uzgoja i smrti, riješeni su praktični zadaci.
Dakle, uz pomoć uzgoja i smrtnih procesa, matematički modeli kontrole različitih procesa, kao i modele mnogih pojava u biologiji, fizici i drugim područjima. Takođe, procesi smrti i reprodukcije široko se koriste u inženjerskoj praksi u proučavanju različitih tehničkih sistema, imaju direktan odnos s mnogim procesima koji se javljaju u okolišu. Markov procesi u osnovi teorije masovne usluge, koji je zauzvrat neophodan u ekonomiji, posebno kada se u njemu upravljaju preduzećima i raznim procesima.
U ovom radu razmatrani su procesi reprodukcije i smrti i formule za izračunavanje graničnih vjerojatnosti, koje se koriste za opisivanje sistema masovnih održavanja sa gubicima i očekivanjima na temelju najjednostavnijih protoka aplikacija. Formule se dobivaju za neke karakteristike.
Lista korištenih izvora
Ventcel, E.S. Teorija slučajnih procesa i njegovih inženjerskih aplikacija: Studentski vodič / E.S. Ventcel, L.A. Ovčov - 2. ed. - M.: "Viša škola", 2000. - 384 str.
Malinkovsky, yu.v. Predavanja o teoriji masovne usluge: Tutorial za univerzitete / yu.v. Malinkovsky. - Gomel: Gsu ih. F. Skirina, - 184 str. (elektronska varijanta)
Barucha Reed, A.T. Elementi teorije Markovskog procesa i njihovih aplikacija / a.t. Barucha_rid - m.: Nauka, 1969. - 512 str.
Sevastyanov, B.A. Na nekim vrstama Markovskog procesa / B.a. Sevastyanov - t. 4, vol. 4 - umn, 1949. - str. 194.
Kolmogorov, A.n. Uvod u teoriju vjerojatnosti: studije. Za univerzitete / I.G. Zhurbenko, A.V. Prokhorov - m.: Nauka, 1982. - 160 s.
Podučavanje
Trebate pomoć za proučavanje koje jezičke teme?
Naši stručnjaci će savjetovati ili imati podučavajuće usluge za predmet interesa.
Pošaljite zahtjev Sa temom upravo sada, naučiti o mogućnosti primitka savjetovanja.
U ovom teorijskom radu razmatrat će se shema kontinuiranih lanaca Markov - takozvani "shema zaduženja i reprodukcije"
Ova je tema izuzetno relevantna zbog velike važnosti Markovskog procesa u istraživanju ekonomskih, ekoloških i bioloških procesa, osim Markovskog procesa na srcu teorije masovne usluge, koji se trenutno aktivno koristi u različitim ekonomskim područjima, uključujući upravljanje procesima u preduzeću.
Markov procesi smrti i reprodukciju široko se koriste u objašnjavanju različitih procesa koji se javljaju u biosferu, ekosustavu itd. Treba napomenuti da je ova vrsta Markovskog procesa precizno primila ime zbog široko rasprostranjene upotrebe u biologiji, posebno simulirajući smrt i reprodukciju pojedinačnih populacija.
U ovom radu, procesi smrti i reprodukcije koristit će se u rješavanju problema, čija je svrha pronaći približni iznos pčela u zasebnom stanovništvu.
Teorijski deo
Kao dio teorijskog dijela bit će napisane algebarske jednadžbe za granične vjerojatnosti. Očito, ako dva kontinuirana lanca Markov imaju iste državne grafike i razlikuju se samo u vrijednostima intenziteta,
možete odmah pronaći granične vjerojatnosti država za svaki od grafova zasebno, dovoljno je sastaviti i riješiti u slovu jednadžbe za jedan od njih, a zatim zamijeniti umjesto odgovarajuće vrijednosti. Za mnoge zajedničke brojke grafikona, linearne jednadžbe lako se rješavaju u pismu.
U ovom radu će se opisati shema neprekidnih lanaca Markov - takozvani "dijagram smrti i reprodukcije".
Kontinuirani lanac Markov naziva se "proces smrti i reprodukcije", ako je njegov grafikon država izgled predstavljen na slici. 1.1, tj. Sve države mogu se izvući u jedan lanac u kojem je svaka srednja stanja (S 2, ..., S N-1) povezana s direktnim i povratnim informacijama sa svakom od susjednih stanja, te ekstremnim stanjima ( S 1, s n) - samo sa jednom susjednom državom.
Za snimanje algebarske jednadžbe za granične verovatnoće država, uzmi nekakav zadatak.
Primjer. Tehnički se uređaj sastoji od tri identična čvorova; Svaki od njih može propasti (odbiti); Odbijeni čvor se odmah počinje oporaviti. Broj stanja sistema po broju neispravnih čvorova:
S 0 - Sva tri čvora su dobra;
S 1 - Jedan čvor je odbio (obnovljen), dva su dobra;
S 2 - dva čvora obnavljaju se, jedan radi;
S 3 - Sva tri čvora obnavljaju se.
Države brojeva prikazane su na slici. 1.2. Iz grafa je jasno da je proces koji teče u sistemu proces "smrti i reprodukcije".
![]()
Shema smrti i reprodukcije vrlo se često nalazi u širokom rasponu praktičnih zadataka; Stoga, to ima smisla u obzir ovu shemu općenito i riješiti odgovarajući sustav algebarske jednadžbe tako da se ubuduće sastanku sa specifičnim procesima pojavljuju u skladu s takvom shemom, ne riješi problem svaki put kada se ponovo ne riješi svaki put, ali za upotrebu gotova rešenje.
Dakle, razmotrite slučajni proces smrti i reprodukcije grafikonom država prikazanih na Sl. 1.3

Pišet ćemo algebarske jednadžbe za vjerojatnosti država. Za prvu državu 1 imamo:
Za drugo stanje S 2, iznosi članova koji odgovaraju dolaznim i odlaznim strelicama jednaki su:
Ali, na osnovu (1.2), možete rezati desno i lijevo jednako jedni drugima članovima i dobiti:
U rečju, za shemu smrti i reprodukcije, članovi koji odgovaraju strelici koji se međusobno stoje jednaki su jednaki:
gde k. uzima sve vrijednosti od 2 do n.
Dakle, ograničenja verovatnoća država r k P 2\u003e ..., r P in Bilo koji dijagram smrti i reprodukcije zadovoljava jednadžbe:
 (1.4)
(1.4)
i stanje normalizacije:
![]() (1.5)
(1.5)
Ovaj sistem ćemo riješiti na sljedeći način: iz prve jednadžbe (1.4) Express p 2:
od drugog uzimajući u obzir (1.6), dobivamo
 (1.7)
(1.7)
od trećeg uzimanja u obzir (1.7):

 (1.8)
(1.8)
Ova formula važi za bilo koji k. od 2 do p.
Obratite pažnju na njegovu strukturu. U brojevniku se nalazi proizvod svih gustoća vjerojatnosti prijelaza (intenziteta) koji stoje po strelicama usmjerenim s lijeva na desno, od početka i do onog koji ulazi u državu S K. ; U nazivniku - rad svih intenziteta , Stojeći uz strijere koje ide na desno ulijevo, opet, od početka i do strelice odlasku iz države S K. . Za k \u003d N. Broj intenziteta stajat će u brojevniku , Stojeći sa svim strelicama odlazak u lijevo desno, a u nazivniku - sve strelice koje idu na desno lijevo.
Dakle, sve su vjerojatnosti izražene kroz jedan od njih :. Zamjena ovih izraza u stanju normalizacije: ![]() . Dobijamo:
. Dobijamo:
Preostale vjerojatnosti izražene su kroz
 (1.10)
(1.10)
Dakle, zadatak "smrti i reprodukcije" rješava se općenitom obliku: Nalaze se ograničenja vjerojatnosti država.
Praktični dio
Markov procesi, posebno smrt i reprodukciju, koriste se za opisivanje radova i analize široke klase sistema sa ograničenim brojem država koji se javljaju ponovljenim prijelazima iz jedne države u drugu pod utjecajem bilo kakvih razloga. U takvim sustavima se javljaju nasumično, skočili su tokom proizvoljnog trenutka vremena kada se pojave neki događaji (teče događaja). U pravilu su dvije vrste: jedan od njih se konvencionalno naziva rođenje objekta, a druga je njegova smrt.
Prirodna reprodukcija pčelinjih porodica - Sa stajališta procesa koji teče u sistemu u trenutnom trenutku moguće je razmotriti vjerojatni proces kada se porodica u određenom trenutku može premjestiti iz radnog stanja u rooh . Ovisno o različitim faktorima, i kontroliranim tehnološkim i slabo kontroliranim biološkim i klimatskim, može se završiti ili vratiti porodicu u radno stanje. Istovremeno, porodica se može više puta preći na jednu stvar, a zatim u drugu državu. Dakle, za opisivanje matematičkog modela procesa, dozvoljeno je primjenjivati \u200b\u200bteoriju homogenih Markovskog procesa.
Intenzitet prelaska porodice pčele u državu rooh je reprodukcija - u velikoj mjeri određeno stopom nakupljanja mladog pčela bez nedostataka. Intenzitet obrnutog tranzicije je "smrt" - povratak porodice u radno stanje, koji, zauzvrat, ovisi o stvarnom razdoblju, odabiru kvara i pčela (formiranje glasnika), količinu nektara sakupljeno, itd.
Verovatnoća prelaska pčele porodice u državu rooth prvo će biti određena intenzitetom procesa koji donose u njemu vodeći do μ, a anti-testere μ koji ovise o tehnologijama koje se koriste za smanjenje tehnologija koje se koriste za smanjenje Put porodica. Slijedom toga, da bi se utjecalo na procese raspravljane, potrebno je promijeniti intenzitet i smjer tokova λ i μ (Sl. 1).

Pojedini modeliranje izbora dijela pčela (povećanje njihove "smrti") pokazala je da je vjerojatnost pojave radne države logaritantna, a vjerojatnost ružičastog je logaritantalno smanjena. U anti-odvijanju - odabir iz porodice od 5-7 hiljada pčela (dva ili tri standardna okvira) - vjerovatnoća rozima bit će 0,05, a vjerojatnost radnog stanja je 0,8; Izbor više od tri okvira sa pčelama smanjuje vjerojatnost vrlo malog iznosa.
Rijeći ćemo praktični zadatak koji se odnosi na proces lopata u pčelama.
Za početak, grafikoli su grafiko na slici 1, s intenzitetima prijelaza na stanje ili drugo.
| |
|
