ओपन लाइब्रेरी - शैक्षिक जानकारी का एक खुला पुस्तकालय। उजागर हवा में उड़ा हुआ पाइथागोरस का पेड़ पाइथागोरस के पेड़ की आकृति बनाने के लिए पुनरावर्ती प्रक्रिया का उपयोग करना

पायथागॉरियन पेड़ एक प्रकार का फ्रैक्टल है जो पायथागॉरियन पैंट्स नामक आकृति पर आधारित है।

अपने प्रसिद्ध प्रमेय को सिद्ध करते हुए, पाइथागोरस ने एक आकृति बनाई जिसमें एक समकोण त्रिभुज के प्रत्येक तरफ वर्ग थे। समय के साथ पाइथागोरस की यह आकृति एक पूरे पेड़ में बदल गई। द्वितीय विश्व युद्ध के दौरान पाइथागोरस वृक्ष का निर्माण करने वाले पहले व्यक्ति ए. बोसमैन थे, जिन्होंने एक साधारण ड्राइंग रूलर का उपयोग किया था।

पायथागॉरियन वृक्ष का एक मुख्य गुण यह है कि जब पहले वर्ग का क्षेत्रफल एक होता है, तो प्रत्येक स्तर पर वर्गों के क्षेत्रफलों का योग भी एक के बराबर होगा। क्लासिक पायथागॉरियन पेड़ का कोण 45 डिग्री होता है, लेकिन अन्य कोणों का उपयोग करके सामान्यीकृत पायथागॉरियन पेड़ का निर्माण करना भी संभव है। ऐसे पेड़ को पाइथागोरस का हवा से उड़ने वाला पेड़ कहा जाता है। यदि आप केवल वे खंड बनाते हैं जो किसी तरह त्रिभुजों के कुछ "केंद्रों" को जोड़ते हैं, तो आपको एक नग्न पायथागॉरियन पेड़ मिलता है।

एक अन्य उदाहरण प्रसिद्ध "पायथागॉरियन वृक्ष" होगा। इसे अक्सर चित्र में दिखाए अनुसार दर्शाया जाता है। 3.2. इस पेड़ के प्रत्येक समकोण त्रिभुज का आंतरिक कोण 45° है।

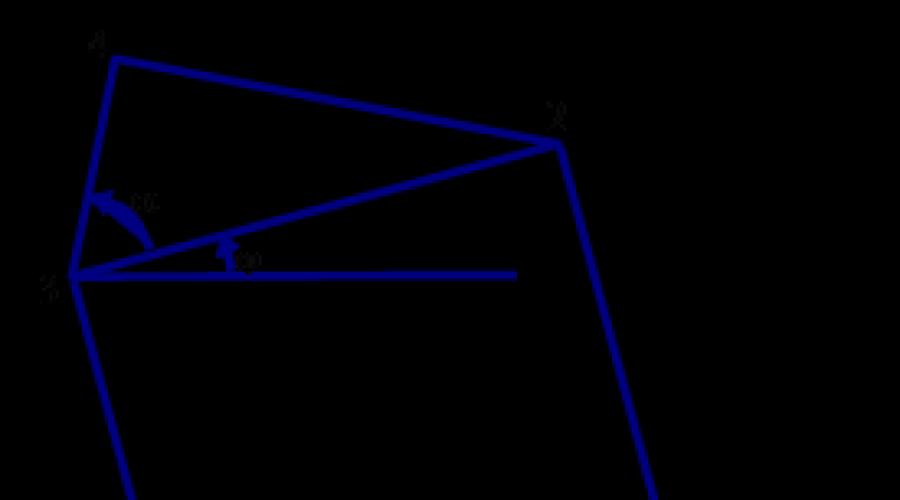
फिर, हम एक अधिक सामान्य प्रोग्राम बनाने के लिए एक यादृच्छिक संख्या जनरेटर का उपयोग करेंगे जो न केवल चावल उत्पन्न कर सकता है। 3.2, लेकिन कम नियमित पेड़ भी पैदा करते हैं। चित्र के लिए कोणों को 45° पर सेट किया गया है। 3.2, सामान्य तौर पर, (45 - के बीच की सीमा के भीतर यादृच्छिक रूप से सेट किया जाएगा) डेल्टा)° और (45+ डेल्टा)° , मूल्य कहां है डेल्टापैरामीटर n के साथ एक इनपुट पैरामीटर के रूप में दिया गया है, जो रिकर्सन गहराई निर्धारित करता है। चित्र में दिखाया गया नियमित संस्करण। 3.2, निर्दिष्ट करके प्राप्त किया गया डेल्टा= 0 और n = 7. चित्र में, पैरामीटर पीपेड़ की जड़ से पत्तियों तक के पथ पर त्रिभुजों की संख्या निर्धारित करता है। कार्यक्रम का मूल पैरामीटर n के साथ पुनरावर्ती फ़ंक्शन sq_and_triangle ("वर्ग और त्रिकोण") होगा, जो पहले तर्क के रूप में पुनरावर्तन की गहराई निर्धारित करता है। यदि पैरामीटर n का मान शून्य से अधिक है, तो वर्ग_और_त्रिकोण का फ़ंक्शन, जैसा कि इसके नाम से पता चलता है, इसके ऊपर एक वर्ग और एक त्रिकोण खींचेगा, और फिर संबंधित नए तर्कों के साथ खुद को दो बार कॉल करेगा, जिनमें से पहला है n-1 पर सेट करें. वर्ग का आकार और स्थिति पूरी तरह से चार मापदंडों द्वारा निर्धारित की जाती है: X0, Y0, a और j (चित्र 3.3 देखें)। एक त्रिभुज बनाने के लिए, आपको कोण a जानना आवश्यक है। डिग्री में व्यक्त यह कोण, 45+विचलन के बराबर है, जहां विचलन यादृच्छिक रूप से चुने गए श्रृंखला के पूर्णांक -डेल्टा, -डेल्टा+आई, ..., डेल्टा में से एक के बराबर है। चित्र में. 3.3 आवश्यक बिंदुओं को क्रमागत संख्या 0,1,2,3,4 अंकित किया गया है। फ़ंक्शन के कॉल में बिंदु O के निर्देशांक X0, Y0 निर्दिष्ट हैं। शेष बिंदुओं की गणना करने के लिए, हम पहले j = 0 के साथ एक सरल स्थिति पर विचार करते हैं, अर्थात, जब वर्ग की भुजा 0 1 क्षैतिज स्थिति में होती है।

इस स्थिति में, बिंदुओं के निर्देशांक निर्धारित करना बहुत आसान है। वे x और y सरणियों में संग्रहीत हैं। फिर पूरी संरचना को कोण j द्वारा बिंदु O के चारों ओर घुमाया जाता है। रोटेशन का परिणाम xx और yy सरणियों में दर्ज किया गया है।

/* PYTH_TREE: पायथागॉरियन पेड़ का एक प्रकार */

#शामिल करें "गणित.h"

#शामिल करें "stdlib.h"

#"समय.एच" शामिल करें

#पीआई 3.1415927 को परिभाषित करें

#शामिल है "stdio.h"

संरचना (फ्लोट xx; फ्लोट yy; int ii;) s;

शून्य pfopen())( fp=fopen("स्क्रैच", "wb"); )

शून्य चाल (फ्लोट x, फ्लोट y)

( s.xx=x; s.yy=y; s.ii=0; /* 0 = पेन अप */ /* 0 = पेन अप */

fwrite(&s, sizeof s, 1, fp);

शून्य पीड्रा (फ्लोट एक्स, फ्लोट वाई)

( s.xx=x; s.yy=y; s.ii=1; /* 1 = पेन डाउन */ /* 1 = पेन डाउन */

fwrite(&s, sizeof s, 1, fp);

शून्य pfclose())( fclose(fp); )

शून्य वर्ग_और_त्रिकोण(int n, फ्लोट x0, फ्लोट y0, फ्लोट a, फ्लोट phi)

(फ्लोट x, y, xx, yy, cphi, sphi, c1, c2, b, c,

अल्फा, कैल्फा, सल्फा;

पूर्णांक मैं, विचलन; /* फाई और अल्फा रेडियन में */

/*डिग्री में डेल्टा*/

यदि(n==0) वापसी; /* कोण फाई और अल्फा रेडियन में */

/* कोण डेल्टा डिग्री में */

विचलन=रैंड()%(2*डेल्टा+1)-डेल्टा;

अल्फ़ा=(45+विचलन)*pi/180.0;

x=x=x0; x=x=x0+a;

य=य=य0; y=y=y0+a;

कैल्फा=कॉस(अल्फा); सल्फा=पाप(अल्फा);

सी=ए*कैल्फा; बी=ए*सल्फा;

/* कोण phi के माध्यम से (x0, y0) के बारे में घूर्णन; */

/* बिंदु (x0, y0) के चारों ओर phi कोण द्वारा घुमाएँ;*/

cphi=cos(phi); स्फी=पाप(फी);

c1=x0-x0*cphi+y0*sphi;

c2=y0-x0*sphi-y0*cphi;

(i=0 के लिए; i<5; i++)

( xx[i]=x[i]*cphi-y[i]*sphi+c1;

yy[i]=x[i]*sphi+y[i]*cphi+c2;

(i=0 के लिए; i<5; i++) pdraw(xx[i],yy[i]);

वर्ग_और_त्रिकोण(n-1, xx, yy, c, phi+alpha);

वर्ग_और_त्रिकोण(n-1, xx, yy, b, phi+alpha-0.5*pi);

pfopen(); समय(&बीज); सरंड((int)बीज);

प्रिंटफ ("डेल्टा कोण को डिग्री (0) में सेट करें< delta < 45) ");

स्कैनफ़ ("%d", &डेल्टा);

प्रिंटफ ("रिकर्सन डेप्थ एन सेट करें"); स्कैनफ़ ("%d", &n);

वर्ग_और_त्रिभुज(n, 0.0, 0.0, 1.0, 0.0);

यह प्रोग्राम एक फ़ाइल बनाता है खरोंचनाजिसे जी प्रोग्राम द्वारा संसाधित किया जाना चाहिए एनप्लॉटव्याख्यान से 2. कार्यक्रम का चित्रमय परिणाम डेल्टा= 30 और एन =चित्र 7 में दिखाया गया है। 3.4.

पायथागॉरियन पेड़ एक प्रकार का फ्रैक्टल है जो पायथागॉरियन पैंट्स नामक आकृति पर आधारित है।

अपने प्रसिद्ध प्रमेय को सिद्ध करते हुए, पाइथागोरस ने एक आकृति बनाई जिसमें एक समकोण त्रिभुज के प्रत्येक तरफ वर्ग थे। समय के साथ पाइथागोरस की यह आकृति एक पूरे पेड़ में बदल गई। द्वितीय विश्व युद्ध के दौरान पाइथागोरस वृक्ष का निर्माण करने वाले पहले व्यक्ति ए. बोसमैन थे, जिन्होंने एक साधारण ड्राइंग रूलर का उपयोग किया था।

पायथागॉरियन वृक्ष का एक मुख्य गुण यह है कि जब पहले वर्ग का क्षेत्रफल एक होता है, तो प्रत्येक स्तर पर वर्गों के क्षेत्रफलों का योग भी एक के बराबर होगा। क्लासिक पायथागॉरियन पेड़ का कोण 45 डिग्री होता है, लेकिन अन्य कोणों का उपयोग करके सामान्यीकृत पायथागॉरियन पेड़ का निर्माण करना भी संभव है। ऐसे पेड़ को पाइथागोरस का हवा से उड़ने वाला पेड़ कहा जाता है। यदि आप केवल वे खंड बनाते हैं जो किसी तरह त्रिभुजों के कुछ "केंद्रों" को जोड़ते हैं, तो आपको एक नग्न पायथागॉरियन पेड़ मिलता है।

मैंडेलब्रॉट सेट फ्रैक्टल का एक उत्कृष्ट उदाहरण है... विकिपीडिया

HTML HTML और HTML5 डायनामिक HTML ... विकिपीडिया

मैंडेलब्रॉट सेट फ्रैक्टल का एक उत्कृष्ट उदाहरण है। फ्रैक्टल (अव्य। फ्रैक्टस क्रश्ड) एक शब्द है जिसका अर्थ है एक ज्यामितीय आकृति जिसमें आत्म-समानता का गुण होता है, अर्थात, कई भागों से बना होता है, जिनमें से प्रत्येक संपूर्ण के समान होता है चित्र... ...विकिपीडिया

लेवी वक्र भग्न. फ्रांसीसी गणितज्ञ पी. लेवी द्वारा प्रस्तावित। यह पता चलता है कि यदि आप / के रूप का आधा वर्ग लेते हैं, और फिर प्रत्येक पक्ष को एक ही टुकड़े से बदल देते हैं, और, इस ऑपरेशन को दोहराते हुए, ... विकिपीडिया में

न्यूटन पूल...विकिपीडिया

केली ग्राफ़ एक ग्राफ़ है जो जनरेटर की एक विशिष्ट प्रणाली वाले समूह से बनाया गया है। केली के नाम पर रखा गया। परिभाषा मान लीजिए कि एक अलग समूह G और जनरेटर S की एक प्रणाली दी गई है। मान लीजिए S = S - 1, यानी प्रत्येक के लिए। प्रणाली के अनुसार समूह जी की केली गणना... ...विकिपीडिया

एक ग्राफ़ जो जेनरेटर की एक समर्पित प्रणाली वाले समूह से बनाया गया है। केली के नाम पर रखा गया। परिभाषा मान लीजिए कि एक अलग समूह और जनरेटर की एक प्रणाली दी गई है। आइए मान लें, अर्थात्, प्रत्येक के लिए। काउंट केली ग्रुप...विकिपीडिया

प्राचीन स्रोतों में प्राचीन ईरानी धर्म। लेख में 5वीं शताब्दी ईसा पूर्व के प्राचीन लेखकों (प्राचीन ग्रीक, लैटिन और आंशिक रूप से अर्मेनियाई और सीरियाई) की जानकारी की समीक्षा शामिल है। इ। छठी शताब्दी ई.पू इ। अचमेनिद युग के ईरानी लोगों के धर्म, पार्थियन और शक्ति के बारे में ... विकिपीडिया

प्राचीन काल में, चौथी, पहली सहस्राब्दी ईसा पूर्व में, यहां रहने वाले लोगों की संस्कृति। ई., मेसोपोटामिया मेसोपोटामिया टाइग्रिस और यूफ्रेट्स (आधुनिक इराक का क्षेत्र), सुमेरियन और अक्कादियन, बेबीलोनियाई और असीरियन, जिन्होंने सुमेर, अक्कड़, बेबीलोनिया के बड़े राज्य बनाए (देखें... ... महान सोवियत विश्वकोश

पुस्तकें

• गर्मियों के अंत में, वेरा ओर्लोव्स्काया। वेरा ओर्लोव्स्काया की नई किताब एट द एंड ऑफ समर अपने विभिन्न रूपों और कुछ शीर्षकों से जो पता चलता है, उससे पाठक को आश्चर्यचकित करती रहती है: पाइथागोरस की फिलॉसफी इन नंबर्स, द ट्री ऑफ ड्रीम, सिम्फनी नंबर 1...
• आर-फ्रैक्टल ज्यामिति के अनुप्रयोगों में एक उपकरण के रूप में कार्य करता है, ए. वी. टोलोक। आर-फ़ंक्शन के सिद्धांत के गणितीय उपकरण का उपयोग फ़ंक्शंस ɷ(x) = 0, x ∈ En द्वारा फ्रैक्टल ज्यामिति की वस्तुओं का वर्णन करने के लिए किया जाता है, जहां ɷ(x) में एकल विश्लेषणात्मक अभिव्यक्ति का रूप होता है। द्वारा…

नमस्ते, फ्रैक्टल और अन्य चीज़ों में रुचि रखने वाले दोस्तों। इस क्षण से, मैं पोस्टों की एक श्रृंखला शुरू कर रहा हूं जिसमें मैं सबसे सरल फ्रैक्टल के निर्माण के सिद्धांतों को समझाऊंगा। अध्ययन करना हमेशा दिलचस्प होता है और मैं इसमें आपकी मदद करूंगा: अब से हम कई, कई फ्रैक्टल जानेंगे। अराजकता के बारे में लेख में लोरेन्ज़ अट्रैक्टर इसका एक उदाहरण था। और आज मैं आपको पायथागॉरियन पेड़ के बारे में बताऊंगा।

तो यह क्या है? पायथागॉरियन पेड़ सबसे सरल फ्रैक्टल है जिसे कागज पर खींचा जा सकता है। लेकिन इस फ्रैक्टल को पाइथागोरस वृक्ष क्यों कहा जाता है? तथ्य यह है कि यहां पाइथागोरस प्रमेय के साथ एक संबंध है - यूक्लिडियन ज्यामिति की नींव में से एक। उसे याद है? मैं आपको याद दिला दूं: a2 + b2 = c2 (पैरों की लंबाई के वर्गों का योग कर्ण की लंबाई के वर्ग के बराबर है)। यह प्रमेय प्राचीन काल से ज्ञात है; वर्तमान में प्रमेय के 400 से अधिक प्रमाण हैं, और केवल पाइथागोरस ही इसे ज्यामितीय रूप से सिद्ध करने वाले पहले व्यक्ति थे। उसने निम्नलिखित आकृति बनाई: उसने एक समकोण त्रिभुज लिया और उसकी भुजाओं पर वर्ग बनाए। इस आकृति को "पायथागॉरियन पैंट" भी कहा जाता है:

यदि हम इस निर्माण को पुनरावर्ती रूप से जारी रखते हैं, तो हम एक पायथागॉरियन पेड़ के साथ समाप्त होते हैं:
पहला पुनरावृत्ति (हमारे पायथागॉरियन पेड़ में कोण 45 डिग्री है):

दूसरा पुनरावृत्ति:

तीसरा पुनरावृत्ति:

दसवाँ पुनरावृत्ति:

पाइथागोरस वृक्ष का एक महत्वपूर्ण गुण: यदि पहले वर्ग का क्षेत्रफल एक के बराबर है, तो प्रत्येक स्तर पर वर्गों के क्षेत्रफलों का योग भी एक के बराबर होगा।
यदि कोण को 45 डिग्री से बदल दिया जाए तो अन्य प्रकार के पाइथागोरस वृक्ष का निर्माण किया जा सकता है।
उदाहरण के लिए, यहाँ तथाकथित "पाइथागोरस का हवा से उड़ने वाला पेड़" है:

कुछ फ्रैक्टल ग्राफ़िक्स जेनरेटर पाइथागोरसियन पेड़ के आधार पर फ्रैक्टल के निर्माण के लिए एक सूत्र लागू करते हैं। यह कार्यान्वयन IFS प्रणाली की बहुत याद दिलाता है, खासकर यदि आप वर्गों को आयतों या लम्बी आकृतियों से बदलते हैं।
आज के लिए बस इतना ही, अगली बैठकों तक, जिसमें कई अन्य दिलचस्प बातें होंगी)