ספרייה פתוחה - ספרייה פתוחה של מידע חינוכי. עץ פיתגורס מרוח חשוף באמצעות הליך רקורסיבי לבניית דמותו של עץ פיתגורס

עץ פיתגורס הוא סוג של פרקטל המבוסס על דמות הידועה בשם מכנסיים פיתגוריים.

בהוכחת המשפט המפורסם שלו, פיתגורס בנה דמות שבה היו ריבועים בכל צד של משולש ישר זווית. עם הזמן, דמותו של פיתגורס הפכה לעץ שלם. הראשון שבנה את עץ הפיתגורס במהלך מלחמת העולם השנייה היה א. בוסמן, באמצעות סרגל ציור רגיל.

אחד המאפיינים העיקריים של העץ הפיתגורי הוא שכאשר שטח הריבוע הראשון הוא אחד, אז בכל רמה סכום שטחי הריבועים יהיה שווה גם הוא לאחד. לעץ הפיתגוראי הקלאסי יש זווית של 45 מעלות, אבל אפשר גם לבנות עץ פיתגורי מוכלל באמצעות זוויות אחרות. עץ כזה נקרא העץ נושב הרוח של פיתגורס. אם אתה מצייר רק את הקטעים המחברים איכשהו "מרכזים" מסוימים של המשולשים, אז אתה מקבל עץ פיתגורי עירום.

דוגמה נוספת תהיה ה"עץ הפיתגורי" המפורסם. לעתים קרובות הוא מתואר כפי שמוצג באיור. 3.2. לכל אחד מהמשולשים הישרים בעץ זה זווית פנימית של 45°.

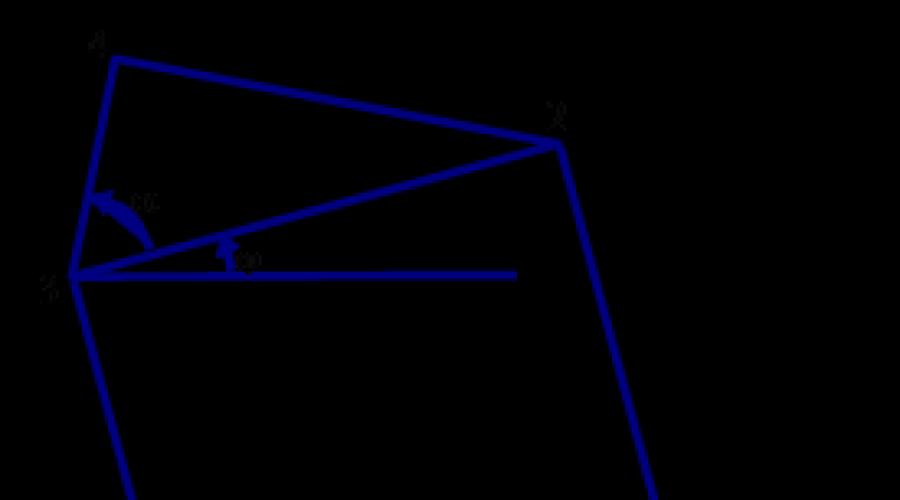
שוב, נשתמש במחולל מספרים אקראיים כדי ליצור תוכנית כללית יותר שיכולה לייצר לא רק אורז. 3.2, אבל גם מייצרים עצים פחות רגילים. זוויות מוגדרות ל-45° עבור איור. 3.2, באופן כללי, יוגדר באופן אקראי בטווח שבין (45 - דֶלתָא)° ו-(45+ דֶלתָא)° , איפה הערך דֶלתָאניתן כפרמטר קלט יחד עם הפרמטר n, הקובע את עומק הרקורסיה. הגרסה הרגילה המוצגת באיור. 3.2, מתקבל על ידי ציון דֶלתָא= 0 ו-n = 7. באיור, הפרמטר פקובע את מספר המשולשים על השביל מהשורש לעלי העץ. ליבת התוכנית תהיה הפונקציה הרקורסיבית square_and_triangle ("ריבוע ומשולש") עם הפרמטר n, הקובע את עומק הרקורסיה, כארגומנט הראשון. אם הערך של הפרמטר n גדול מאפס, אזי הפונקציה של square_and_triangle, כשמה כן היא, תצייר ריבוע ומשולש מעליו, ואז תקרא לעצמה פעמיים נוספות עם הארגומנטים החדשים המתאימים, הראשון שבהם הוא מוגדר ל-n-1. הגודל והמיקום של הריבוע נקבעים לחלוטין על ידי ארבעה פרמטרים: X0, Y0, a ו-j (ראה איור 3.3). כדי לצייר משולש, אתה צריך לדעת את הזווית א. זווית זו, המבוטאת במעלות, שווה ל-45+סטייה, כאשר הסטייה שווה לאחד המספרים השלמים של הסדרה -delta, -delta+I, ..., delta, שנבחר באקראי. באיור. 3.3 הנקודות הדרושות ממוספרים מספרים עוקבים 0,1,2,3,4. הקואורדינטות X0, Y0 של נקודה O מצוינות בקריאה לפונקציה. כדי לחשב את הנקודות הנותרות, נבחן תחילה מצב פשוט יותר עם j = 0, כלומר, כאשר הצלע 0 1 של הריבוע תופסת מיקום אופקי.

/* PYTH_TREE: וריאנט של העץ הפיתגורי */

#include "math.h"

#include "stdlib.h"

#include "time.h"

#define pi 3.1415927

#include "stdio.h"

struct (float xx; float yy; int ii;) s;

void pfopen())( fp=fopen("scratch", "wb"); )

void pmove(float x,float y)

( s.xx=x; s.yy=y; s.ii=0; /* 0 = עט למעלה */ /* 0 = עט למעלה */

fwrite(&s, sizeof s, 1, fp);

void pdraw(float x,float y)

( s.xx=x; s.yy=y; s.ii=1; /* 1 = עט למטה */ /* 1 = עט למטה */

fwrite(&s, sizeof s, 1, fp);

void pfclose())( fclose(fp); )

void square_and_triangle(int n,float x0,float y0, float a, float phi)

( לצוף x, y, xx, yy, cphi, sphi, c1, c2, b, c,

אלפא, קלפה, סלפה;

int i, סטייה; /* פי ואלפא ברדיאנים */

/* דלתא במעלות */

if(n==0) return; /* זוויות פי ואלפא ברדיאנים */

/* דלתא זווית במעלות */

deviation=rand()%(2*delta+1)-delta;

alpha=(45+סטייה)*pi/180.0;

x=x=x0; x=x=x0+a;

y=y=y0; y=y=y0+a;

calpha=cos(alpha); salpha=sin(alpha);

c=a*calpha; b=a*salpha;

/* סיבוב בערך (x0, y0) דרך זווית phi; */

/* סובב סביב הנקודה (x0, y0) לפי זווית phi;*/

cphi=cos(phi); sphi=sin(phi);

c1=x0-x0*cphi+y0*sphi;

c2=y0-x0*sphi-y0*cphi;

עבור (i=0; i<5; i++)

( xx[i]=x[i]*cphi-y[i]*sphi+c1;

yy[i]=x[i]*sphi+y[i]*cphi+c2;

עבור (i=0; i<5; i++) pdraw(xx[i],yy[i]);

square_and_triangle(n-1, xx, yy, c, phi+alpha);

square_and_triangle(n-1, xx, yy, b, phi+alpha-0.5*pi);

pfopen(); time(&seed); srand((int)seed);

printf(" הגדר זווית דלתא במעלות (0< delta < 45) ");

scanf("%d", &delta);

printf(" הגדר עומק רקורסיה n "); scanf("%d", &n);

square_and_triangle(n, 0.0, 0.0, 1.0, 0.0);

תוכנית זו יוצרת קובץ שריטהאשר חייב להיות מעובד על ידי תוכנית G ENPLOTמתוך הרצאה 2. תוצאה גרפית של התוכנית עבור דֶלתָא= 30 ו n = 7 מוצג באיור. 3.4.

עץ פיתגורס הוא סוג של פרקטל המבוסס על דמות הידועה בשם מכנסיים פיתגוריים.

בהוכחת המשפט המפורסם שלו, פיתגורס בנה דמות שבה היו ריבועים בכל צד של משולש ישר זווית. עם הזמן, דמותו של פיתגורס הפכה לעץ שלם. הראשון שבנה את עץ הפיתגורס במהלך מלחמת העולם השנייה היה א. בוסמן, באמצעות סרגל ציור רגיל.

אחד המאפיינים העיקריים של העץ הפיתגורי הוא שכאשר שטח הריבוע הראשון הוא אחד, אז בכל רמה סכום שטחי הריבועים יהיה שווה גם הוא לאחד. לעץ הפיתגוראי הקלאסי יש זווית של 45 מעלות, אבל אפשר גם לבנות עץ פיתגורי מוכלל באמצעות זוויות אחרות. עץ כזה נקרא העץ נושב הרוח של פיתגורס. אם אתה מצייר רק את הקטעים המחברים איכשהו "מרכזים" מסוימים של המשולשים, אז אתה מקבל עץ פיתגורי עירום.

סט מנדלברוט הוא דוגמה קלאסית של פרקטל... ויקיפדיה

HTML HTML ו-HTML5 דינמי HTML ... ויקיפדיה

סט מנדלברוט הוא דוגמה קלאסית לפרקטל.פרקטל (lat. fractus כתוש) הוא מונח שמשמעותו דמות גיאומטרית בעלת תכונת הדמיון העצמי, כלומר מורכבת מכמה חלקים שכל אחד מהם דומה לכלל. דמות... ... ויקיפדיה

לוי עקומת פרקטל. הוצע על ידי המתמטיקאי הצרפתי פ. לוי. מסתבר שאם לוקחים חצי ריבוע מהצורה /, ואז מחליפים כל צד באותו שבר, וחוזרים על הפעולה הזו ב... ויקיפדיה

ניוטון בריכות ... ויקיפדיה

גרף Cayley הוא גרף הבנוי מקבוצה עם מערכת נבדלת של גנרטורים. נקרא על שם קיילי. הגדרה ניתן לתת קבוצה בדיד G ומערכת של מחוללים S. נניח S = S − 1, כלומר לכל אחד מהם. ספירת קיילי של קבוצה G לפי השיטה... ... ויקיפדיה

גרף הבנוי מקבוצה עם מערכת ייעודית של גנרטורים. נקרא על שם קיילי. הגדרה אפשר לתת קבוצה בדידה ומערכת של גנרטורים. בואו נניח, כלומר, לכל אחד. קבוצת הרוזן קיילי ... ויקיפדיה

דת איראנית עתיקה במקורות עתיקים. המאמר מכיל סקירה של מידע מחברים קדומים (יווני עתיק, לטינית ובחלקו ארמני וסורי) מהמאה ה-5 לפני הספירה. ה. המאה ה-6 לספירה ה. על דתם של העמים האיראנים של התקופה האחמנית, הפרתים והכוח ... ויקיפדיה

תרבות העמים שישבו בה בימי קדם, באלף ה-4 ה-1 לפני הספירה. e., מסופוטמיה מסופוטמיה חידקל ופרת (שטחה של עיראק המודרנית), שומרים ואכדים, בבלים ואשורים, שיצרו את המדינות הגדולות של שומר, אכד, בבל (ראה... ... האנציקלופדיה הסובייטית הגדולה

ספרים

• בסוף הקיץ, ורה אורלובסקיה. ספרה החדש של ורה אורלובסקיה בסוף הקיץ ממשיך להדהים את הקורא בשלל צורותיו ובמה שמציעים חלק מהכותרים: הפילוסופיה של פיתגורוס במספרים, עץ החלום, סימפוניה מס' 1...
• R-מתפקד כמכשיר ביישומים של גיאומטריה פרקטלית, A.V. Tolok. המנגנון המתמטי של תורת פונקציות R משמש לתיאור אובייקטים של גיאומטריה פרקטלית על ידי הפונקציות ɷ(x) = 0, x ∈ En, כאשר ל-ɷ(x) יש צורה של ביטוי אנליטי יחיד. על ידי…

שלום, חברים המתעניינים בפרקטלים ועוד. החל מרגע זה, אני משיק סדרת פוסטים בהם אסביר את העקרונות של בניית הפרקטלים הפשוטים ביותר. זה תמיד מעניין ללמוד ואני אעזור לך בזה: מעכשיו נדע הרבה הרבה פרקטלים. המושך של לורנץ במאמר על כאוס היה דוגמה לכך. והיום אספר לכם על העץ הפיתגורי.

אז מה זה? עץ פיתגורס הוא הפרקטל הפשוט ביותר שניתן לצייר על נייר. אבל למה הפרקטל הזה נקרא עץ פיתגורס? העובדה היא שיש כאן קשר למשפט פיתגורס - אחד מיסודות הגיאומטריה האוקלידית. זוכרים אותה? תן לי להזכיר לך: a2 + b2 = c2 (סכום ריבועי אורכי הרגליים שווה לריבוע אורך התחתון). משפט זה היה ידוע עוד מימי קדם; יש כיום יותר מ-400 הוכחות למשפט, ורק פיתגורס היה הראשון שהוכיח אותו מבחינה גיאומטרית. הוא בנה את הדמות הבאה: הוא לקח משולש ישר זווית וצייר ריבועים על צלעותיו. דמות זו נקראת גם "מכנסיים פיתגוריים":

אם נמשיך את הבנייה הזו באופן רקורסיבי, נקבל עץ פיתגורי:
איטרציה ראשונה (בעץ הפיתגורי שלנו הזווית היא 45 מעלות):

איטרציה שנייה:

איטרציה שלישית:

איטרציה עשירית:

תכונה חשובה של העץ הפיתגורי: אם שטח הריבוע הראשון שווה לאחד, אז בכל רמה סכום שטחי הריבועים יהיה שווה גם לאחד.
אם הזווית משתנה מ-45 מעלות, ניתן לבנות סוגים אחרים של עץ פיתגורס.
הנה, למשל, מה שנקרא "עץ פיתגורס נושב הרוח":

חלק ממחוללי גרפיקה פרקטלית מיישמים נוסחה לבניית פרקטל המבוססת על עץ פיתגורס. יישום זה מזכיר מאוד את מערכת ה-IFS, במיוחד אם מחליפים את הריבועים במלבנים או צורות מוארכות.
זה הכל להיום, עד לפגישות הבאות, בהן יהיו פרקטלים מעניינים רבים אחרים)