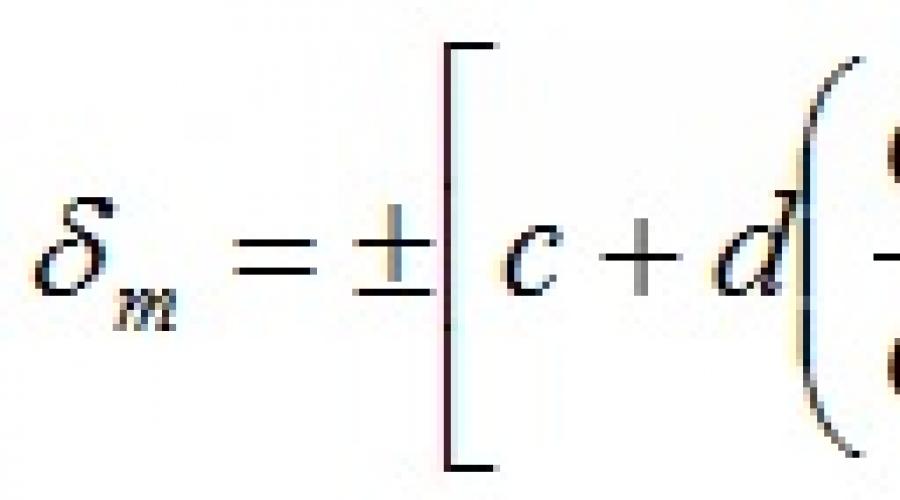
Gotovo je nemoguće apsolutno tačno odrediti pravu vrijednost fizičke veličine, jer svaka mjerna operacija povezana je s brojnim greškama ili, drugim riječima, netačnostima. Razlozi za greške mogu biti veoma različiti. Njihova pojava može biti povezana s nepreciznostima u izradi i podešavanju mjernog uređaja, zbog fizičkih karakteristika objekta koji se proučava (na primjer, kada se mjeri prečnik žice neujednačene debljine, rezultat nasumično zavisi od izbor mjesta mjerenja), slučajni razlozi, itd.

Zadatak eksperimentatora je da smanji njihov utjecaj na rezultat, ali i da ukaže koliko je dobiveni rezultat blizak pravom.

Postoje koncepti apsolutne i relativne greške.

Ispod apsolutna greška mjerenja će razumjeti razliku između rezultata mjerenja i prave vrijednosti izmjerene veličine:

∆x i =x i -x i (2)

gdje je ∆x i apsolutna greška i-tog mjerenja, x i _ je rezultat i-tog mjerenja, x i prava vrijednost izmjerene vrijednosti.

Rezultat bilo kojeg fizičkog mjerenja obično se piše u obliku:

gdje je srednja aritmetička vrijednost izmjerene vrijednosti, najbliža pravoj vrijednosti (vrijednost x i≈ će biti prikazana u nastavku), je apsolutna greška mjerenja.

Jednakost (3) treba shvatiti na način da se prava vrijednost mjerene veličine nalazi u intervalu [ - , + ].

Apsolutna greška je dimenzionalna veličina; ima istu dimenziju kao i izmjerena veličina.

Apsolutna greška ne karakteriše u potpunosti tačnost merenja. U stvari, ako mjerimo segmente dužine 1 m i 5 mm sa istom apsolutnom greškom ± 1 mm, tačnost mjerenja će biti neuporediva. Stoga se uz apsolutnu grešku mjerenja izračunava i relativna greška.

Relativna greška mjerenja je omjer apsolutne greške i same izmjerene vrijednosti:

Relativna greška je bezdimenzionalna veličina. Izražava se u procentima:

U gornjem primjeru, relativne greške su 0,1% i 20%. One se značajno razlikuju jedna od druge, iako su apsolutne vrijednosti iste. Relativna greška daje informaciju o tačnosti

Greške u mjerenju

Prema prirodi ispoljavanja i razlozima nastanka grešaka, one se mogu podeliti u sledeće klase: instrumentalne, sistematske, nasumične i promašene (grube greške).

Greške su uzrokovane ili kvarom uređaja, ili kršenjem metodologije ili eksperimentalnih uvjeta, ili su subjektivne prirode. U praksi se definišu kao rezultati koji se oštro razlikuju od drugih. Da biste otklonili njihovu pojavu, potrebno je biti oprezan i temeljit pri radu s uređajima. Rezultati koji sadrže greške moraju se isključiti iz razmatranja (odbaciti).

Greške na instrumentima. Ako je mjerni uređaj u ispravnom stanju i podešen, tada se na njemu mogu vršiti mjerenja sa ograničenom preciznošću određenom vrstom uređaja. Uobičajeno je da se greška instrumenta pokazivača instrumenta smatra jednakom polovini najmanjeg dijela njegove skale. Kod instrumenata sa digitalnim očitavanjem, greška instrumenta se izjednačava sa vrednošću jedne najmanje cifre skale instrumenta.

Sistematske greške su greške čija su veličina i predznak konstantni za čitav niz mjerenja izvršenih istom metodom i korištenjem istih mjernih instrumenata.

Prilikom izvođenja mjerenja važno je ne samo uzeti u obzir sistematske greške, već je potrebno osigurati i njihovo otklanjanje.

Sistematske greške se konvencionalno dijele u četiri grupe:

1) greške čija je priroda poznata i njihova veličina se može prilično precizno odrediti. Takva greška je, na primjer, promjena mjerene mase u zraku, koja ovisi o temperaturi, vlažnosti, tlaku zraka itd.;

2) greške čija je priroda poznata, ali je veličina same greške nepoznata. Takve greške uključuju greške uzrokovane mjernim uređajem: neispravnost samog uređaja, skala koja ne odgovara nultoj vrijednosti ili klasu tačnosti uređaja;

3) greške u čije postojanje se ne može sumnjati, ali njihova veličina često može biti značajna. Takve greške se najčešće javljaju u složenim mjerenjima. Jednostavan primjer takve greške je mjerenje gustine nekog uzorka koji sadrži šupljinu unutra;

4) greške uzrokovane karakteristikama samog mjernog objekta. Na primjer, kada se mjeri električna provodljivost metala, od potonjeg se uzima komad žice. Do grešaka može doći ako postoji bilo kakav nedostatak u materijalu - pukotina, zadebljanje žice ili nehomogenost koja mijenja njenu otpornost.

Slučajne greške su greške koje se nasumično mijenjaju u predznaku i veličini pod identičnim uvjetima ponovljenih mjerenja iste veličine.

Povezane informacije.

Nijedno mjerenje nije bez grešaka, ili, preciznije, vjerovatnoća mjerenja bez grešaka se približava nuli. Vrste i uzroci grešaka su veoma raznoliki i na njih utiču mnogi faktori (slika 1.2).

Opšte karakteristike faktora uticaja mogu se sistematizovati sa različitih gledišta, na primer, prema uticaju navedenih faktora (slika 1.2).

Na osnovu rezultata mjerenja, greške se mogu podijeliti u tri vrste: sistematske, slučajne i greške.

Sistematske greške zauzvrat, oni su podijeljeni u grupe zbog njihovog pojavljivanja i prirode njihovog ispoljavanja. One se mogu eliminisati na razne načine, na primjer, uvođenjem amandmana.

pirinač. 1.2

Slučajne greške uzrokovane su složenim skupom promjenjivih faktora, obično nepoznatih i teško analiziranih. Njihov uticaj na rezultat merenja može se smanjiti, na primer, ponovljenim merenjima uz dalju statističku obradu rezultata dobijenih metodom teorije verovatnoće.

TO misses To uključuje grube greške koje proizlaze iz naglih promjena u eksperimentalnim uvjetima. Ove greške su takođe slučajne prirode i, kada se jednom identifikuju, moraju biti eliminisane.

Tačnost mjerenja se ocjenjuje greškama mjerenja, koje se prema prirodi pojave dijele na instrumentalne i metodološke, a prema načinu proračuna na apsolutne, relativne i redukovane.

Instrumental Grešku karakterizira klasa tačnosti mjernog uređaja, koja je navedena u njegovom pasošu u obliku normaliziranih glavnih i dodatnih grešaka.

Metodički greška je zbog nesavršenosti mjernih metoda i instrumenata.

Apsolutno greška je razlika između izmjerenih G u i pravih G vrijednosti veličine, određena formulom:

Δ=ΔG=G u -G

Imajte na umu da veličina ima dimenziju mjerene veličine.

Relativno greška se nalazi iz jednakosti

δ=±ΔG/G u ·100%

Dato greška se izračunava po formuli (klasa tačnosti mjernog uređaja)

δ=±ΔG/G norma ·100%

gdje je G norme normalizirajuća vrijednost mjerene veličine. Uzima se jednako:

a) konačnu vrijednost skale instrumenta, ako je nulta oznaka na ivici ili izvan skale;

b) zbir konačnih vrijednosti skale bez uzimanja u obzir znakova, ako se nulta oznaka nalazi unutar skale;

c) dužina skale, ako je skala neujednačena.

Klasa tačnosti uređaja utvrđuje se tokom njegovog testiranja i predstavlja standardizovanu grešku izračunatu pomoću formula

γ=±ΔG/G norme ·100%, akoΔG m =konst

gdje je ΔG m najveća moguća apsolutna greška uređaja;

G k – konačna vrijednost granice mjerenja uređaja; c i d su koeficijenti koji uzimaju u obzir projektne parametre i svojstva mjernog mehanizma uređaja.

Na primjer, za voltmetar sa konstantnom relativnom greškom vrijedi jednakost

δ m =±c

Relativne i smanjene greške povezane su sljedećim ovisnostima:

a) za bilo koju vrijednost smanjene greške

δ=±γ·G norme/G u

b) za najveću redukovanu grešku

δ=±γ m ·G norme/G u

Iz ovih odnosa proizilazi da pri mjerenju, na primjer voltmetrom, u kolu na istoj vrijednosti napona, što je niži izmjereni napon, to je veća relativna greška. A ako je ovaj voltmetar pogrešno odabran, tada relativna greška može biti srazmjerna vrijednosti G n , što je neprihvatljivo. Imajte na umu da u skladu s terminologijom problema koji se rješavaju, na primjer, pri mjerenju napona G = U, kada se mjeri struja C = I, slovne oznake u formulama za izračunavanje grešaka moraju biti zamijenjene odgovarajućim simbolima.

Primjer 1.1. Voltmetar sa vrijednostima γ m = 1,0%, U n = G norme, G k = 450 V, izmjeriti napon U u jednak 10 V. Procijenimo greške mjerenja.

Rješenje.

Odgovori. Greška mjerenja je 45%. Sa takvom greškom, izmjereni napon se ne može smatrati pouzdanim.

Ako su mogućnosti za odabir uređaja (voltmetra) ograničene, metodološka greška se može uzeti u obzir amandmanom izračunatom pomoću formule

Primjer 1.2. Izračunajte apsolutnu grešku voltmetra V7-26 pri mjerenju napona u DC kolu. Klasa tačnosti voltmetra određena je maksimalnom redukovanom greškom γ m =±2,5%. Granica voltmetarske skale koja se koristi u radu je U norma = 30 V.

Rješenje. Apsolutna greška se izračunava pomoću poznatih formula:

(pošto se redukovana greška, po definiciji, izražava formulom , onda odavde možete pronaći apsolutnu grešku:

Odgovori.ΔU = ±0,75 V.

Važni koraci u procesu mjerenja su obrada rezultata i pravila zaokruživanja. Teorija približnih proračuna omogućava, znajući stepen tačnosti podataka, da se proceni stepen tačnosti rezultata i pre izvođenja radnji: da se odaberu podaci sa odgovarajućim stepenom tačnosti, dovoljnim da obezbedi potrebnu tačnost rezultata, ali ne prevelik da spasi kalkulator od beskorisnih proračuna; racionalizovati sam proces izračunavanja, oslobađajući ga od onih proračuna koji neće uticati na tačne brojke i rezultate.

Prilikom obrade rezultata primjenjuju se pravila zaokruživanja.

• Pravilo 1. Ako je prva odbačena znamenka veća od pet, tada se posljednja zadržana znamenka povećava za jedan.

• Pravilo 2. Ako je prva odbačena znamenka manja od pet, onda se ne povećava.

• Pravilo 3. Ako je odbačena cifra pet, a iza nje nema značajnih cifara, zaokruživanje se vrši na najbliži paran broj, tj. zadnja pohranjena znamenka ostaje ista ako je parna i povećava se ako nije parna.

Ako se iza broja pet nalaze značajne brojke, zaokruživanje se vrši prema pravilu 2.

Primjenom pravila 3 na zaokruživanje jednog broja, ne povećavamo preciznost zaokruživanja. Ali uz brojna zaokruživanja, višak brojeva će se pojaviti otprilike jednako često kao i nedovoljni brojevi. Međusobna kompenzacija greške će osigurati najveću točnost rezultata.

Poziva se broj koji očigledno premašuje apsolutnu grešku (ili joj je u najgorem slučaju jednak). maksimalna apsolutna greška.

Veličina maksimalne greške nije sasvim sigurna. Za svaki približni broj mora biti poznata njegova maksimalna greška (apsolutna ili relativna).

Kada nije direktno naznačeno, podrazumeva se da je maksimalna apsolutna greška polovina jedinice poslednje upisane cifre. Dakle, ako je dat približni broj od 4,78 bez navođenja maksimalne greške, tada se pretpostavlja da je maksimalna apsolutna greška 0,005. Kao rezultat ovog sporazuma, uvijek možete učiniti bez navođenja maksimalne greške broja zaokruženog prema pravilima 1-3, odnosno, ako je približni broj označen slovom α, tada

gdje je Δn maksimalna apsolutna greška; i δ n je maksimalna relativna greška.

Osim toga, prilikom obrade rezultata koristimo se pravila za pronalaženje greške zbir, razlika, proizvod i količnik.

• Pravilo 1. Maksimalna apsolutna greška zbira jednaka je zbiru maksimalnih apsolutnih grešaka pojedinačnih članova, ali kod značajnog broja grešaka članova obično dolazi do međusobne kompenzacije grešaka, pa je prava greška zbira samo u izuzetnim slučajevima. slučajevima poklapa se sa maksimalnom greškom ili joj je blizu.

• Pravilo 2. Maksimalna apsolutna greška razlike jednaka je zbiru maksimalnih apsolutnih grešaka one koja se smanjuje ili oduzima.

Maksimalna relativna greška može se lako pronaći izračunavanjem maksimalne apsolutne greške.

• Pravilo 3. Maksimalna relativna greška sume (ali ne i razlika) leži između najmanje i najveće relativne greške članova.

Ako svi pojmovi imaju istu maksimalnu relativnu grešku, onda zbir ima istu maksimalnu relativnu grešku. Drugim riječima, u ovom slučaju tačnost zbira (u procentima) nije inferiorna u odnosu na tačnost termina.

Za razliku od zbira, razlika približnih brojeva može biti manje precizna od umanjenja i oduzimanja. Gubitak preciznosti je posebno veliki kada se minuend i subtrahend malo razlikuju jedan od drugog.

• Pravilo 4. Maksimalna relativna greška proizvoda približno je jednaka zbiru maksimalnih relativnih grešaka faktora: δ=δ 1 +δ 2, ili, preciznije, δ=δ 1 +δ 2 +δ 1 δ 2 gde je δ relativna greška proizvoda, δ 1 δ 2 - faktori relativne greške.

Bilješke:

1. Ako se pomnože približni brojevi sa istim brojem značajnih cifara, onda u proizvodu treba zadržati isti broj značajnih cifara. Posljednja pohranjena znamenka neće biti potpuno pouzdana.

2. Ako neki faktori imaju značajnije cifre od drugih, onda prije množenja, prve treba zaokružiti, zadržavajući u njima onoliko cifara koliko je najmanje tačan faktor ili još jedan (kao rezervni), čuvanje daljih cifara je beskorisno.

3. Ako se traži da proizvod dva broja ima unaprijed određen broj koji je potpuno pouzdan, tada u svakom od faktora broj tačnih cifara (dobijenih mjerenjem ili proračunom) mora biti za jednu više. Ako je broj faktora veći od dva i manji od deset, tada u svakom od faktora broj tačnih cifara za potpunu garanciju mora biti dvije jedinice veći od potrebnog broja tačnih cifara. U praksi je sasvim dovoljno uzeti samo jednu dodatnu cifru.

• Pravilo 5. Maksimalna relativna greška kvocijenta je približno jednaka zbroju maksimalnih relativnih grešaka dividende i delioca. Tačna vrijednost maksimalne relativne greške uvijek premašuje približnu. Postotak viška je približno jednak maksimalnoj relativnoj grešci razdjelnika.

Primjer 1.3. Pronađite maksimalnu apsolutnu grešku količnika 2,81: 0,571.

Rješenje. Maksimalna relativna greška dividende je 0,005:2,81=0,2%; djelitelj – 0,005:0,571=0,1%; privatni – 0,2% + 0,1% = 0,3%. Maksimalna apsolutna greška količnika će biti približno 2,81: 0,571·0,0030=0,015

To znači da u količniku 2,81:0,571=4,92 treća značajna cifra nije pouzdana.

Odgovori. 0,015.

Primjer 1.4. Izračunajte relativnu grešku očitavanja voltmetra spojenog prema strujnom kolu (slika 1.3), koja se dobija ako pretpostavimo da voltmetar ima beskonačno veliki otpor i da ne unosi izobličenja u mjerni krug. Klasificirajte grešku mjerenja za ovaj problem.

pirinač. 1.3

Rješenje. Označimo očitanja stvarnog voltmetra sa AND, a voltmetra sa beskonačno velikim otporom sa AND ∞. Potrebna relativna greška

primeti, to

onda dobijamo

Pošto su R I >>R i R > r, razlomak u nazivniku posljednje jednakosti je mnogo manji od jedan. Stoga možete koristiti približnu formulu , vrijedi za λ≤1 za bilo koje α. Uz pretpostavku da je u ovoj formuli α = -1 i λ= rR (r+R) -1 R And -1, dobijamo δ ≈ rR/(r+R) R And.

Što je veći otpor voltmetra u odnosu na vanjski otpor kruga, manja je greška. Ali uslov R<

Odgovori. Sistematska metodološka greška.

Primjer 1.5. Kolo jednosmerne struje (slika 1.4) uključuje sledeće uređaje: A – ampermetar tipa M 330, klasa tačnosti K A = 1,5 sa granicom merenja I k = 20 A; A 1 - ampermetar tip M 366, klasa tačnosti K A1 = 1,0 sa granicom merenja I k1 = 7,5 A. Naći najveću moguću relativnu grešku u merenju struje I 2 i moguće granice njene stvarne vrednosti, ako su instrumenti pokazali da je I = 8 ,0A. i I 1 = 6.0A. Klasificirajte mjerenje.

pirinač. 1.4

Rješenje. Određujemo struju I 2 iz očitavanja uređaja (bez uzimanja u obzir njihovih grešaka): I 2 =I-I 1 =8,0-6,0=2,0 A.

Nađimo apsolutne module greške ampermetara A i A 1

Za A imamo jednakost za ampermetar

Nađimo zbir modula apsolutne greške:

Prema tome, najveća moguća vrijednost iste vrijednosti, izražena u razlomcima ove vrijednosti, jednaka je 1. 10 3 – za jedan uređaj; 2·10 3 – za drugi uređaj. Koji će od ovih uređaja biti najprecizniji?

Rješenje. Preciznost uređaja karakteriše recipročna vrednost greške (što je uređaj tačniji, to je greška manja), tj. za prvi uređaj to će biti 1/(1 . 10 3) = 1000, za drugi – 1/(2 . 10 3) = 500. Imajte na umu da je 1000 > 500. Dakle, prvi uređaj je dvostruko precizniji od drugi.

Do sličnog zaključka može se doći provjerom konzistentnosti grešaka: 2. 10 3 / 1. 10 3 = 2.

Odgovori. Prvi uređaj je dvostruko precizniji od drugog.

Primjer 1.6. Pronađite zbir približnih mjera uređaja. Pronađite broj tačnih znakova: 0,0909 + 0,0833 + 0,0769 + 0,0714 + 0,0667 + 0,0625 + 0,0588+ 0,0556 + 0,0526.

Rješenje. Zbrajanjem svih rezultata mjerenja dobijamo 0,6187. Maksimalna maksimalna greška sume je 0,00005·9=0,00045. To znači da je u posljednjoj četvrtoj znamenki sume moguća greška do 5 jedinica. Stoga iznos zaokružujemo na treću cifru, tj. hiljaditih, dobijamo 0,619 - rezultat u kojem su svi predznaci tačni.

Odgovori. 0,619. Broj tačnih cifara je tri decimale.

Problem je formuliran na sljedeći način: neka željena količina z određene preko drugih veličina a, b, c, ... dobiveno direktnim mjerenjem

z = f (a, b, c,...) (1.11)

Potrebno je pronaći prosječnu vrijednost funkcije i grešku njenih mjerenja, tj. pronađite interval pouzdanosti

sa pouzdanošću a i relativnom greškom.

Što se tiče, nalazi se zamjenom u desnu stranu (11) umjesto na a, b, c,...njihove prosječne vrijednosti

3. Procijenite polovičnu širinu intervala povjerenja za rezultat indirektnih mjerenja

,

gdje su derivati... izračunati na

4. Odrediti relativnu grešku rezultata

5. Ako je zavisnost z od a, b, c,... ima oblik , Gdje k, l, m‒ bilo koje realne brojeve, onda prvo morate pronaći relativno greška

i onda apsolutno .

6. Upišite konačni rezultat u obrazac

z = ± Dz , ε = …% na a = … .

Bilješka:

Prilikom obrade rezultata direktnih mjerenja morate se pridržavati sljedećeg pravila: numeričke vrijednosti svih izračunatih veličina moraju sadržavati jednu znamenku više od izvornih (eksperimentalno utvrđenih) količina.

Za indirektna mjerenja, proračuni se rade prema pravila približnih proračuna:

Pravilo 1. Prilikom sabiranja i oduzimanja približnih brojeva, morate:

a) odaberite termin u kojem sumnjiva cifra ima najveću cifru;

b) zaokružiti sve ostale pojmove na sljedeću cifru (jedna rezervna cifra se zadržava);

c) izvršiti sabiranje (oduzimanje);

d) kao rezultat, odbacite posljednju cifru zaokruživanjem (cifra sumnjive cifre rezultata poklapa se sa najvišom od cifara sumnjivih cifara pojmova).

primjer: 5,4382·10 5 – 2,918·10 3 + 35,8 + 0,064.

U ovim brojevima posljednje značajne cifre su sumnjive (netačne su već odbačene). Zapišimo ih u obliku 543820 – 2918 + 35,8 + 0,064.

Može se vidjeti da u prvom članu sumnjivi broj 2 ima najveću cifru (desetice). Zaokružimo sve ostale brojeve na sljedeću cifru i saberemo, dobijemo

543820 – 2918 + 36 + 0 = 540940 = 5,4094 10 5.

Pravilo 2. Prilikom množenja (dijeljenja) približnih brojeva morate:

a) odaberite broj(e) sa najmanjim brojem značajnih cifara ( ZNAČAJNI – brojevi različiti od nule i nule između njih);

b) zaokružiti preostale brojeve tako da imaju jednu značajniju cifru (jedna rezervna cifra se zadržava) od onih dodijeljenih u koraku a;

c) pomnožiti (podijeliti) dobijene brojeve;

d) kao rezultat, ostavite onoliko značajnih cifara koliko je bilo u broju(ovima) sa najmanjim brojem značajnih cifara.

primjer: .

Pravilo 3. Kada se podigne na stepen, prilikom izdvajanja korijena, rezultat zadržava onoliko značajnih cifara koliko ih ima u originalnom broju.

primjer: .

Pravilo 4. Prilikom pronalaženja logaritma broja, mantisa logaritma mora imati onoliko značajnih znamenki koliko ih ima u originalnom broju:

primjer: .

U finalnom snimku apsolutno greške treba samo ostaviti jedna značajna figura. (Ako se ispostavi da je ova cifra 1, onda se druga cifra pohranjuje iza nje).

Prosječna vrijednost se zaokružuje na istu cifru kao i apsolutna greška.

Na primjer: V= (375,21 0,03) cm 3 = (3,7521 0,0003) cm 3.

I= (5.530 0.013) A, A = J.

Radni nalog

Određivanje prečnika cilindra.

1. Koristeći čeljust, izmjerite prečnik cilindra 7 puta (na različitim mjestima i smjerovima). Zapišite rezultate u tabelu.

Greške u izmjerenim i tabeliranim veličinama određuju greške DH avg indirektno određene vrijednosti, a najveći doprinos DH avg daju najmanje tačne vrijednosti, koje imaju najveću relativnu grešku d. Stoga je za povećanje tačnosti indirektnih mjerenja potrebno postići jednaku tačnost direktnih mjerenja.

(d A, d B, d C, ...).

Pravila za pronalaženje grešaka u indirektnim mjerenjima:

1. Naći prirodni logaritam date funkcije

ln(X = f(A,B,C,…));

2. Naći ukupni diferencijal (po svim varijablama) iz pronađenog prirodnog logaritma date funkcije;

3. Predznak diferencijala d zamijeniti predznakom apsolutne greške D;

4. Zamijenite sve "minuse" suočene sa apsolutnim greškama DA, DB, DC, ... do "profesionalaca".

Rezultat je formula za najveću relativnu grešku d x indirektno izmjerena vrijednost X:

d x = = j (A avg, B prosječno, C prosječno, ..., DA prosječno, DB prosječno, DC prosječno, ...).(18)

Prema pronađenoj relativnoj grešci d x odrediti apsolutnu grešku indirektnog mjerenja:

DX av = d x. X avg . (19)

Rezultat indirektnih mjerenja ispisuje se u standardnom obliku i prikazuje na numeričkoj osi:

X = (X prosječno ± DH prosječno), jedinica. (20)

Primjer:

Pronađite vrijednosti relativne i prosječne greške fizičke veličine L, posredno određeno formulom:

, (21)

Gdje π, g, t, k, α, β– veličine čije se vrijednosti mjere ili uzimaju iz referentnih tabela i unose u tabelu rezultata mjerenja i tabelarnih podataka (slično Tablici 1).

1. Izračunajte prosječnu vrijednost L avg, zamjenjujući prosječne vrijednosti iz tabele u (21) – π avg, g avg, t avg, k avg, α avg, β avg.

2. Odredite najveću relativnu grešku δ L:

a). Formula logaritma (21):

b). Rezultirajući izraz (22) se diferencira:

c) Zamijenite znak diferencijala d sa Δ, a "minus" ispred apsolutne greške sa "plus", i dobijete izraz za najveću relativnu grešku δ L:

d). Zamjenom prosječnih vrijednosti ulaznih veličina i njihovih grešaka iz tabele rezultata mjerenja u rezultirajući izraz, izračunajte δ L.

3. Zatim izračunajte apsolutnu grešku ΔL avg:

Rezultat se bilježi u standardnom obliku i grafički prikazuje na osi L:

, jedinica promijeniti

ELEMENTARNE PROCJENE GREŠKE MJERENJA

Mjerenje je eksperimentalno pronalaženje vrijednosti fizičke veličine uz pomoć posebnih tehničkih sredstava - mjera, mjernih instrumenata.

Mjera je mjerno sredstvo koje reproducira fizičku veličinu date veličine – mjernu jedinicu, njenu višestruku ili frakcijsku vrijednost. Na primjer, težine 1 kg, 5 kg, 10 kg.

Mjerni uređaj je mjerni instrument dizajniran za generiranje signala mjerne informacije u obliku dostupnom za direktnu percepciju posmatrača. Merni uređaj vam omogućava da direktno ili indirektno uporedite izmerenu vrednost sa merama. Mjerenja se također dijele na direktna i indirektna.

U direktnim mjerenjima, željena vrijednost veličine se nalazi direktno iz osnovnih (eksperimentalnih) podataka.

U indirektnim mjerenjima, željena vrijednost neke veličine se nalazi na osnovu poznatog odnosa između ove veličine i veličina koje su podvrgnute direktnim mjerenjima. Princip mjerenja je skup fizičkih pojava na kojima se mjerenja zasnivaju.

Metoda mjerenja je skup tehnika za korištenje principa i mjernih instrumenata. Vrijednost fizičke veličine, koja bi idealno odražavala u kvalitativnom i kvantitativnom smislu odgovarajuće svojstvo datog objekta, je prava vrijednost fizičke veličine. Vrijednost fizičke veličine pronađena njenim mjerenjem je rezultat mjerenja.

Odstupanje rezultata mjerenja od prave vrijednosti izmjerene vrijednosti je greška mjerenja.

Apsolutna greška mjerenja je greška mjerenja, izražena u jedinicama mjerene vrijednosti i jednaka razlici između rezultata i prave vrijednosti izmjerene vrijednosti. Odnos apsolutne greške i prave vrednosti merene veličine je relativna greška merenja.

Doprinos grešci mjerenja uključuje greške u mjernim instrumentima (instrumentalna ili instrumentalna greška), nesavršenost mjerne metode, grešku u očitavanju na skali instrumenta, vanjski utjecaj na sredstva i objekte mjerenja i kašnjenje ljudske reakcije na svjetlosne i zvučne signale. .

Na osnovu prirode njihovog ispoljavanja, greške se dele na sistematske i slučajne. Slučajni događaj je događaj koji se, s obzirom na dati skup faktora, može, ali i ne mora dogoditi.

Slučajna greška je komponenta greške mjerenja koja se nasumično mijenja s ponovljenim mjerenjima iste količine. Karakteristična karakteristika slučajnih grešaka je promena veličine i znaka greške u konstantnim uslovima merenja.

Sistematska greška je komponenta greške mjerenja koja ostaje konstantna ili se prirodno mijenja s ponovljenim mjerenjima iste veličine. Sistematske greške se u principu mogu otkloniti ispravkama i upotrebom preciznijih instrumenata i metoda (iako u praksi nije uvijek lako otkriti sistematske greške). Nemoguće je isključiti slučajne greške u pojedinačnim mjerenjima; matematička teorija slučajnih pojava (teorija vjerovatnoće) omogućava samo da se uspostavi razumna procjena njihove veličine.

Greške direktnih mjerenja

Pretpostavimo da su sistematske greške isključene i da su greške u rezultatima mjerenja samo slučajne. Označimo slovima rezultate mjerenja fizičke veličine, čija je prava vrijednost jednaka . Naznačene su apsolutne greške rezultata pojedinačnih mjerenja:

Zbrajanjem lijeve i desne strane jednakosti (1) dobijamo:

(2)

Teorija slučajnih grešaka zasniva se na pretpostavkama potvrđenim iskustvom:

greške mogu poprimiti neprekidan niz vrijednosti;

kod velikog broja mjerenja, slučajne greške iste veličine, ali različitih predznaka, javljaju se podjednako često;

vjerovatnoća greške se smanjuje kako se njena veličina povećava. Takođe je neophodno da greške budu male u odnosu na izmerenu vrednost i nezavisne.

Prema pretpostavci (1), sa brojem mjerenja n   dobijamo

,

Međutim, broj dimenzija je uvijek konačan i ostaje nepoznato. Ali u praktične svrhe, dovoljno je eksperimentalno pronaći vrijednost fizičke veličine toliko blizu pravoj da može se koristiti umjesto true. Pitanje je kako ocijeniti stepen ove aproksimacije?

Prema teoriji vjerovatnoće, aritmetička sredina serije mjerenja pouzdaniji od rezultata pojedinačnih mjerenja, jer jednako su vjerovatna slučajna odstupanja od prave vrijednosti u različitim smjerovima. Vjerovatnoća pojavljivanja vrijednosti a i u intervalu širine 2a i podrazumijeva se kao relativna učestalost pojavljivanja vrijednosti a i koje spadaju u interval 2a i prema broju svih prikazanih vrijednosti a i sa brojem eksperimenata (mjerenja) koji teži beskonačnosti. Očigledno, vjerovatnoća pouzdanog događaja jednaka je jedan, vjerovatnoća nemogućeg događaja jednaka je nuli, tj. 0    100%.

Vjerovatnoća da je željena vrijednost (njena prava vrijednost) sadržana u intervalu (a - a, a + a) nazvat će se vjerovatnoća povjerenja (pouzdanost) , a odgovarajući  interval (a - a, a + a) - interval pouzdanosti; Što je manja greška a, to je manja vjerovatnoća da se izmjerena vrijednost nalazi u intervalu definisanom ovom greškom. Tačna je i suprotna izjava: što je rezultat manje pouzdan, to je interval pouzdanosti željene vrijednosti uži.

Za veliko n (praktično za n  100), poluširina intervala povjerenja za datu pouzdanost  jednaka je

, (3)

gdje je K() = 1 pri  = 0,68; K() = 2 pri  = 0,95; K() = 3 pri  = 0,997.

Uz mali broj mjerenja, što se najčešće sreće u studentskoj laboratorijskoj praksi, koeficijent K() u (3) zavisi ne samo od , već i od broja mjerenja n. Stoga, u prisustvu samo slučajne greške, uvijek ćemo pronaći polovinu širine intervala povjerenja koristeći formulu

(4)

U (4) koeficijent t  n naziva se Student koeficijent. Za  = 0,95 usvojeno u studentskom praktičnom radu, vrijednosti t  n su sljedeće:

Vrijednost se naziva srednja kvadratna greška aritmetičke sredine serije mjerenja.

Greška instrumenta ili mjere obično je naznačena u pasošu ili simbolom na skali instrumenta. Obično se pod greškom instrumenta  podrazumijeva polovična širina intervala unutar kojeg izmjerena vrijednost može biti sadržana sa vjerovatnoćom mjerenja od 0,997, ako je greška mjerenja nastala samo zbog greške instrumenta. Kao opštu (ukupnu) grešku rezultata merenja prihvatićemo sa verovatnoćom  = 0,95

Apsolutna greška vam omogućava da odredite u kom znaku dobijenog rezultata je sadržana nepreciznost. Relativna greška daje informaciju o tome koliki je udio (procenat) izmjerene vrijednosti greška (polovina širine intervala povjerenja).

Zapisujemo konačni rezultat serije direktnih mjerenja vrijednosti a 0 u obliku

.

Na primjer

(6)

Dakle, svaka fizička veličina pronađena eksperimentalno mora biti predstavljena:

Dimenzije se zovu ravno, ako se vrijednosti veličina određuju direktno instrumentima (na primjer, mjerenje dužine ravnalom, određivanje vremena štopericom itd.). Dimenzije se zovu indirektno, ako je vrijednost mjerene veličine određena direktnim mjerenjem drugih veličina koje su povezane sa specifičnim odnosom koji se mjeri.

Slučajne greške u direktnim mjerenjima

Apsolutna i relativna greška. Neka se to sprovede N mjerenja iste količine x u nedostatku sistematske greške. Pojedinačni rezultati mjerenja su sljedeći: x 1 ,x 2 , …,x N. Prosječna vrijednost izmjerene vrijednosti je odabrana kao najbolja:

Apsolutna greška jednog mjerenja naziva se razlika oblika:

.

Prosječna apsolutna greška N jedinične mjere:

(2)

pozvao prosječna apsolutna greška.

Relativna greška Odnos prosječne apsolutne greške i prosječne vrijednosti mjerene veličine naziva se:

. (3)

Greške instrumenta u direktnim mjerenjima

Ako nema posebnih uputstava, greška instrumenta je jednaka polovini njegove vrijednosti dijeljenja (ravnalo, čaša).

Greška instrumenata opremljenih noniusom jednaka je vrijednosti podjele nonija (mikrometar - 0,01 mm, kaliper - 0,1 mm).

Greška vrijednosti tablice jednaka je polovini jedinice posljednje znamenke (pet jedinica sljedećeg reda nakon posljednje značajne znamenke).

Greška električnih mjernih instrumenata izračunava se prema klasi tačnosti WITH naznačeno na skali instrumenta:

Na primjer:
I
,

Gdje U max I I max– granica mjerenja uređaja.

Greška uređaja sa digitalnim displejom jednaka je jednoj od poslednjih cifara prikaza.

Nakon procjene slučajnih i instrumentalnih grešaka, u obzir se uzima ona čija je vrijednost veća.

Proračun grešaka u indirektnim mjerenjima

Većina mjerenja su indirektna. U ovom slučaju, željena vrijednost X je funkcija nekoliko varijabli A,b, c… , čije se vrijednosti mogu pronaći direktnim mjerenjem: X = f( a, b, c…).

Aritmetička sredina rezultata indirektnih mjerenja bit će jednaka:

X = f( a, b, c…).

Jedan od načina da se izračuna greška je razlikovanje prirodnog logaritma funkcije X = f( a, b, c...). Ako je, na primjer, željena vrijednost X određena relacijom X = , onda nakon logaritma dobijamo: lnX = ln a+ln b+ln( c+ d).

Diferencijal ovog izraza ima oblik:

.

U odnosu na izračunavanje približnih vrijednosti, može se zapisati za relativnu grešku u obliku:

 =
. (4)

Apsolutna greška se izračunava pomoću formule:

H = H(5)

Dakle, izračunavanje grešaka i izračunavanje rezultata za indirektna mjerenja vrši se sljedećim redoslijedom:

1) Izmjerite sve količine uključene u početnu formulu da biste izračunali konačni rezultat.

2) Izračunajte srednje aritmetičke vrijednosti svake mjerene vrijednosti i njihove apsolutne greške.

3) Zamijenite prosječne vrijednosti svih izmjerenih vrijednosti u originalnu formulu i izračunajte prosječnu vrijednost željene vrijednosti:

X = f( a, b, c…).

4) Logaritam originalnu formulu X = f( a, b, c...) i zapišite izraz za relativnu grešku u obliku formule (4).

5) Izračunajte relativnu grešku  = .

6) Izračunajte apsolutnu grešku rezultata koristeći formulu (5).

7) Konačan rezultat se piše kao:

Apsolutne i relativne greške najjednostavnijih funkcija date su u tabeli: