Kako pronaći apsolutne i relativne greške. Proračun grešaka direktnih mjerenja

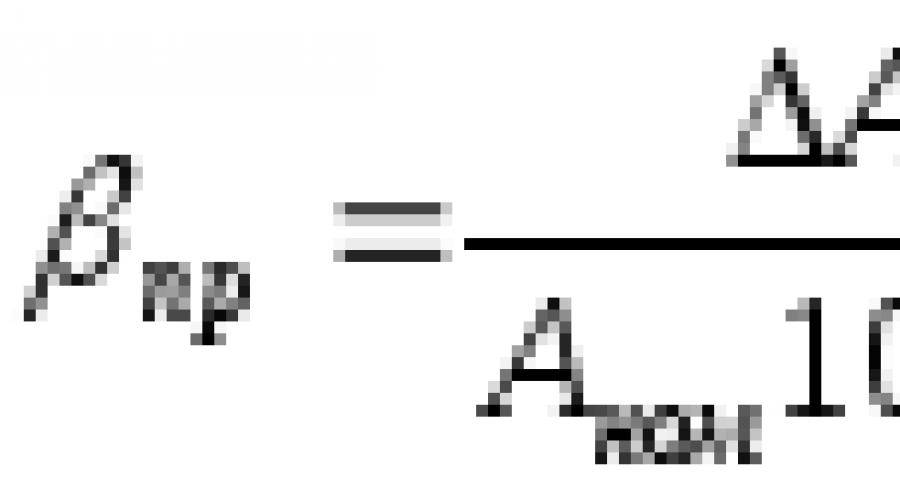
Rezultat mjerenja fizičke veličine uvijek se razlikuje od prave vrijednosti za određeni iznos, koji se naziva greška

KLASIFIKACIJA:

1. Po načinu izražavanja: apsolutno, redukovano i relativno

2. Po izvoru: metodološki i instrumentalni.

3. Prema uslovima i uzrocima nastanka: glavni i dodatni

4. Po prirodi promjena: sistematske i nasumične.

5. Ovisno o ulaznoj izmjerenoj vrijednosti: aditivno i multiplikativno

6. Ovisno o inerciji: statički i dinamički.

13. Apsolutne, relativne i smanjene greške.

Apsolutna greška je razlika između izmjerene i stvarne vrijednosti mjerene veličine:

gdje je A izmjereno, A je izmjerena i stvarna vrijednost; ΔA - apsolutna greška.

Apsolutna greška se izražava u jedinicama izmjerene vrijednosti. Apsolutna greška uzeta sa suprotnim predznakom naziva se korekcija.

Relativnogreška p je jednak omjeru apsolutne greške ΔA i stvarne vrijednosti izmjerene vrijednosti i izražava se kao postotak:

Datogreška mjernog instrumenta je odnos apsolutne greške i nominalne vrijednosti. Nominalna vrijednost za uređaj sa jednostranom skalom jednaka je gornjoj granici mjerenja, za uređaj sa dvostranom skalom (sa nulom u sredini) - aritmetički zbir gornjih granica mjerenja:

pr.br.

14. Metodološke, instrumentalne, sistematske i slučajne greške.

Greška metode nastaje zbog nesavršenosti primijenjene metode mjerenja, nepreciznosti formula i matematičkih ovisnosti koje opisuju ovu metodu mjerenja, kao i uticaja mjernog instrumenta na objekt čija se svojstva mijenjaju.

Instrumentalna greška(greška instrumenta) nastaje zbog konstrukcijskih karakteristika mjernog uređaja, netačnosti kalibracije i skale, kao i nepravilne instalacije mjernog uređaja.

Instrumentalna greška, po pravilu, je naznačena u pasošu za mjerni instrument i može se ocijeniti numerički.

Sistematska greška- konstantna ili prirodno promenljiva greška tokom ponovljenih merenja iste količine pod istim uslovima merenja. Na primjer, greška koja se javlja pri mjerenju otpora amper-voltmetrom uzrokovana je praznom baterijom.

Slučajna greška- greška mjerenja čija se priroda mijenja tokom ponovljenih mjerenja iste količine pod istim uslovima je slučajna. Na primjer, greška u brojanju tokom nekoliko ponovljenih mjerenja.

Uzrok slučajne greške je istovremeno djelovanje mnogih slučajnih faktora, od kojih svaki pojedinačno ima mali učinak.

Slučajna greška se može proceniti i delimično smanjiti pravilnom obradom metodama matematičke statistike, kao i metodama verovatnoće.

15. Osnovne i dodatne, statičke i dinamičke greške.

Osnovna greška- greška koja se javlja u normalnim uslovima upotrebe mjernog instrumenta (temperatura, vlažnost, napon napajanja itd.), koji su standardizovani i specificirani u standardima ili tehničkim specifikacijama.

Dodatna greška je uzrokovano odstupanjem jedne ili više utjecajnih veličina od normalne vrijednosti. Na primjer, promjene temperature okoline, promjene vlažnosti, fluktuacije napona napajanja. Vrijednost dodatne greške je standardizovana i navedena u tehničkoj dokumentaciji za mjerne instrumente.

Statička greška- greška pri mjerenju vremenske konstante vrijednosti. Na primjer, greška mjerenja napona konstantne struje tokom mjerenja.

Dinamička greška- greška mjerenja vremenski promjenjive veličine. Na primjer, greška u mjerenju komutiranog istosmjernog napona, uzrokovana prolaznim procesima tokom komutacije, kao i ograničena brzina mjernog uređaja.

Često se u životu moramo suočiti s različitim približnim količinama. Približni proračuni su uvijek proračuni s nekom greškom.

Koncept apsolutne greške

Apsolutna greška približne vrijednosti je veličina razlike između tačne i približne vrijednosti.
To jest, trebate oduzeti približnu vrijednost od tačne vrijednosti i uzeti rezultujući broj po modulu. Dakle, apsolutna greška je uvijek pozitivna.

Kako izračunati apsolutnu grešku

Hajde da pokažemo kako bi to moglo izgledati u praksi. Na primjer, imamo graf određene vrijednosti, neka je parabola: y=x^2.

Iz grafikona možemo odrediti približnu vrijednost u nekim tačkama. Na primjer, kod x=1,5 vrijednost y je približno jednaka 2,2 (y≈2,2).

Koristeći formulu y=x^2 možemo pronaći tačnu vrijednost u tački x=1,5 y= 2,25.

Sada izračunajmo apsolutnu grešku naših mjerenja. |2,25-2,2|=|0,05| = 0,05.

Apsolutna greška je 0,05. U takvim slučajevima takođe kažu da je vrednost izračunata sa tačnošću od 0,05.

Često se dešava da se tačna vrijednost ne može uvijek pronaći, pa stoga nije uvijek moguće pronaći apsolutnu grešku.

Na primjer, ako izračunamo udaljenost između dvije točke pomoću ravnala, ili vrijednost ugla između dvije prave pomoću kutomjera, onda ćemo dobiti približne vrijednosti. Ali tačnu vrijednost je nemoguće izračunati. U ovom slučaju možemo odrediti broj tako da vrijednost apsolutne greške ne može biti veća.

U primjeru s ravnalom, to će biti 0,1 cm, jer je vrijednost podjele na ravnalu 1 milimetar. U primjeru za kutomjer, 1 stepen jer je skala kutomjera stepenovana na svakom stepenu. Dakle, vrijednosti apsolutne greške u prvom slučaju su 0,1, au drugom slučaju 1.

Trebate pomoć oko studija?

Neka veličina koja se mjeri ima poznatu vrijednost X. Naravno, pojedinačne vrijednosti ove količine pronađene su tokom procesa mjerenja x1 , x2 ,… xn očigledno nisu sasvim tačni, tj. ne podudaraju X. Zatim vrijednost
biće apsolutna greška i th dimenzija. Ali od pravog značenja rezultata X, obično nije poznato, tada se umjesto X koristi stvarna procjena apsolutne greške prosjek
, koji se izračunava po formuli:

Međutim, za male veličine uzoraka, umjesto
poželjno koristiti medijana. medijana (ja) je vrijednost slučajne varijable x takva da polovina rezultata ima vrijednost manju od, a druga polovina ima vrijednost veću od Meh. Da izračunam Meh rezultati su poredani uzlaznim redom, odnosno formiraju takozvani varijacioni niz. Za neparan broj mjerenja n, medijan je jednak vrijednosti srednjeg člana serije. Na primjer,
za n=3

Za paran n, vrijednost Meh jednak polovini zbira vrijednosti dva prosječna rezultata. Na primjer,
za n=4

Za obračun s koristite nezaokružene rezultate analize s nepreciznim zadnjim decimalnim mjestom.
Sa veoma velikim brojem uzorka ( n>
) slučajne greške se mogu opisati korištenjem normalnog Gaussovog zakona raspodjele. At small n distribucija se može razlikovati od normalne. U matematičkoj statistici ova dodatna nepouzdanost je eliminisana modifikovanom simetrijom t-distribucija. Postoji neki koeficijent t, nazvan Studentov koeficijent, koji u zavisnosti od broja stepeni slobode ( f) i vjerovatnoća povjerenja ( R) omogućava vam prelazak sa uzorka na populaciju.
Standardna devijacija prosječnog rezultata
određena formulom:

Magnituda

je interval pouzdanosti srednje vrijednosti
. Za serijske analize obično se pretpostavlja R= 0,95.

Tabela 1. Vrijednosti studentskog koeficijenta ( t)

Primjer 1 . Iz deset određivanja sadržaja mangana u uzorku potrebno je izračunati standardnu ​​devijaciju jedne analize i interval pouzdanosti prosječne vrijednosti Mn%: 0,69; 0,68; 0,70; 0,67; 0,67; 0,69; 0,66; 0,68; 0,67; 0,68.
Rješenje. Pomoću formule (1) izračunava se prosječna vrijednost analize

Prema tabeli 1 (Dodatak) pronaći Student koeficijent za f=n-1=9 (P=0,95) t=2,26 i izračunati interval pouzdanosti srednje vrijednosti. Tako je prosječna vrijednost analize određena intervalom (0,679 ± 0,009) % Mn.

Primjer 2 . Prosjek od devet mjerenja pritiska vodene pare nad rastvorom uree na 20°C je 2,02 kPa. Standardna devijacija uzorka mjerenja s = 0,04 kPa. Odredite širinu intervala pouzdanosti za prosjek od devet i jedno mjerenje koje odgovara vjerovatnoći pouzdanosti od 95%.
Rješenje. Koeficijent t za nivo pouzdanosti od 0,95 i f = 8 je 2,31. S obzirom na to

I
, mi nalazimo:

- širina će biti pouzdana. interval za prosječnu vrijednost

- širina će biti pouzdana. interval za mjerenje jedne vrijednosti

Ako postoje rezultati analize uzoraka različitog sadržaja, onda iz parcijalnih prosjeka s usrednjavanjem možete izračunati ukupnu prosječnu vrijednost s. Imati m uzorke i za svako provođenje uzorka nj paralelne definicije, rezultati su predstavljeni u obliku tabele:

Prosječna greška se izračunava iz jednačine:

sa stepenima slobode f = n – m, gdje je n ukupan broj definicija, n=m. nj.

Primjer 2. Izračunajte prosječnu grešku u određivanju mangana u pet čeličnih uzoraka različitog sadržaja. Vrijednosti analize, % Mn:
1. 0,31; 0,30; 0,29; 0,32.
2. 0,51; 0,57; 0,58; 0,57.
3. 0,71; 0,69; 0,71; 0,71.
4. 0,92; 0,92; 0,95; 0,95.
5. 1,18; 1,17; 1,21; 1,19.
Rješenje. Pomoću formule (1) pronalaze se prosječne vrijednosti u svakom uzorku, zatim se izračunavaju kvadratne razlike za svaki uzorak, a greška se izračunava pomoću formule (5).
1)
= (0,31 + 0,30 + 0,29 + 0,32)/4 = 0,305.
2)
= (0,51 + 0,57 + 0,58 + 0,57)/4 = 0,578.
3)
= (0,71+ 0,69 + 0,71 + 0,71)/4 = 0,705.
4)
= (0,92+0,92+0,95+0,95)/4 =0,935.
5)
= (1,18 + 1,17 + 1, 21 + 1,19)/4 = 1,19.

Vrijednosti kvadrata razlika
1) 0,0052 +0,0052 +0,0152 +0,0152 =0,500.10 -3 .
2) 0,0122 +0,0082 +0,0022 +0,0082 =0,276.10 -3 .
3) 0,0052 + 0,0152 + 0,0052 + 0,0052 = 0,300.10 -3 .
4) 0,0152+ 0,0152 + 0,0152 + 0,0152 = 0,900.10 -3 .
5) 0,012 +0,022 +0,022 + 02 = 0,900.10 -3 .
Prosječna greška za f = 4,5 – 5 = 15

s= 0,014% (apsolutno pri f=15 stepeni slobode).

Kada se provedu dva paralelna određivanja za svaki uzorak i vrijednosti se pronađu X" I X", za uzorke jednačina se pretvara u izraz.

3.1 Greška aritmetičke sredine. Kao što je ranije navedeno, mjerenja u osnovi ne mogu biti apsolutno tačna. Stoga se prilikom mjerenja postavlja zadatak da se odredi interval u kojem se najvjerovatnije nalazi prava vrijednost izmjerene vrijednosti. Ovaj interval je naznačen u obliku apsolutne greške mjerenja.

Ako pretpostavimo da su grube greške u merenjima eliminisane, a sistematske greške minimizirane pažljivim podešavanjem instrumenata i cele instalacije i nisu presudne, onda će rezultati merenja uglavnom sadržati samo slučajne greške, koje su naizmenične veličine. Dakle, ako se izvrši više ponovljenih mjerenja iste veličine, tada je najvjerovatnija vrijednost mjerene veličine njena aritmetička srednja vrijednost:

Prosječna apsolutna greška naziva se aritmetička sredina modula apsolutne greške pojedinačnih mjerenja:

Posljednja nejednakost se obično piše kao konačni rezultat mjerenja na sljedeći način:

pri čemu se apsolutna greška a cf mora izračunati (zaokružiti) sa tačnošću od jedne ili dvije značajne brojke. Apsolutna greška pokazuje koji znak broja sadrži netačnosti, dakle u izrazu za a Wed Ostavljaju sve ispravne brojeve i jedan sumnjiv. To jest, prosječna vrijednost i prosječna greška izmjerene vrijednosti moraju se izračunati na cifru iste cifre. Na primjer: g = (9,78 ± 0,24) m/s 2 .

Relativna greška. Apsolutna greška određuje interval najvjerovatnijih vrijednosti izmjerene vrijednosti, ali ne karakterizira stepen tačnosti izvršenih mjerenja. Na primjer, udaljenost između naseljenih mjesta, mjerena sa tačnošću od nekoliko metara, može se klasifikovati kao vrlo tačna mjerenja, dok će mjerenje prečnika žice sa tačnošću od 1 mm, u većini slučajeva, biti vrlo približna mjerenja.

Stepen tačnosti izvršenih mjerenja karakterizira relativna greška.

Prosjek relativna greška ili jednostavno relativna greška mjerenja je omjer prosječne apsolutne greške mjerenja i prosječne vrijednosti mjerene veličine:

Relativna greška je bezdimenzionalna veličina i obično se izražava u postocima.

3.2 Greška metode ili greška instrumenta. Srednja aritmetička vrijednost izmjerene vrijednosti je bliža pravoj, što se više mjerenja vrši, dok apsolutna greška mjerenja sa povećanjem broja teži vrijednosti koja je određena metodom mjerenja i tehničkim karakteristikama upotrebljenih instrumenata.

Greška metode ili se greška instrumenta može izračunati iz jednokratnog mjerenja, znajući klasu tačnosti uređaja ili druge podatke u tehničkom pasošu uređaja, koji označavaju ili klasu tačnosti uređaja ili njegovu apsolutnu ili relativnu grešku mjerenja.

Klasa tačnosti uređaj izražava u procentima nominalnu relativnu grešku uređaja, odnosno relativnu grešku merenja kada je izmerena vrednost jednaka graničnoj vrednosti za dati uređaj

Apsolutna greška uređaja ne zavisi od vrednosti merene veličine.

Relativna greška uređaja (po definiciji):

(10)

iz čega se vidi da što je vrednost merene veličine bliža granici merenja datog uređaja, to je manja relativna greška instrumenta. Stoga se preporučuje odabir uređaja tako da izmjerena vrijednost bude 60-90% vrijednosti za koju je uređaj dizajniran. Kada radite s instrumentima s više opsega, također treba nastojati osigurati da se očitavanje vrši u drugoj polovini skale.

Prilikom rada sa jednostavnim instrumentima (ravnalo, čaša, itd.), čija tačnost i klase greške nisu određene tehničkim karakteristikama, apsolutna greška direktnih mjerenja uzima se jednakom polovini vrijednosti podjele ovog instrumenta. (Vrijednost podjela je vrijednost izmjerene veličine kada su očitanja instrumenta jedno podjeljenje).

Instrumentalna greška indirektnih mjerenja može se izračunati koristeći približna pravila izračuna. Proračun greške indirektnih mjerenja zasniva se na dva uslova (pretpostavke):

1. Apsolutne greške merenja su uvek veoma male u poređenju sa izmerenim vrednostima. Stoga se apsolutne greške (u teoriji) mogu smatrati beskonačno malim povećanjem mjerenih veličina i mogu se zamijeniti odgovarajućim diferencijalima.

2. Ako je fizička veličina, koja je određena indirektno, funkcija jedne ili više direktno mjerenih veličina, tada je apsolutna greška funkcije, zbog beskonačno malih priraštaja, također beskonačno mala veličina.

Pod ovim pretpostavkama, apsolutne i relativne greške mogu se izračunati koristeći dobro poznate izraze iz teorije diferencijalnog računa funkcija mnogih varijabli:

	(11)
	(12)

Apsolutne greške direktnih mjerenja mogu imati predznak plus ili minus, ali koji je nepoznat. Stoga se pri određivanju grešaka smatra najnepovoljnijim slučajem kada greške u direktnim mjerenjima pojedinačnih veličina imaju isti predznak, odnosno apsolutna greška ima maksimalnu vrijednost. Stoga, pri izračunavanju priraštaja funkcije f(x 1,x 2,…,x n) prema formulama (11) i (12), parcijalni priraštaji se moraju dodati u apsolutnoj vrijednosti. Dakle, koristeći aproksimaciju Dh i ≈ dx i, i izrazi (11) i (12), za beskonačno male inkremente Da može se napisati:

	(13)
	(14)

ovdje: A - indirektno izmjerena fizička veličina, odnosno određena računskom formulom, Da- apsolutnu grešku njegovog mjerenja, x 1, x 2,...x n; Dh 1, Dx 2,..., Dh n,- fizičke veličine direktnih mjerenja i njihove apsolutne greške, respektivno.

Dakle: a) apsolutna greška metode indirektnog mjerenja jednaka je zbiru apsolutnih vrijednosti proizvoda parcijalnih izvoda mjerne funkcije i odgovarajućih apsolutnih grešaka direktnih mjerenja; b) relativna greška metode indirektnog mjerenja jednaka je zbiru diferencijalnih modula iz prirodnog logaritma mjerne funkcije, utvrđene proračunskom formulom.

Izrazi (13) i (14) vam omogućavaju da izračunate apsolutne i relativne greške na osnovu jednokratnog mjerenja. Imajte na umu da je za smanjenje izračunavanja pomoću ovih formula dovoljno izračunati jednu od grešaka (apsolutnu ili relativnu), a drugu izračunati koristeći jednostavan odnos između njih:

U praksi se češće koristi formula (13), jer se prilikom uzimanja logaritma formule za izračunavanje proizvodi različitih veličina pretvaraju u odgovarajuće zbrojeve, a stepen i eksponencijalne funkcije se pretvaraju u proizvode, što uvelike pojednostavljuje proces diferencijacije. .

Za praktične smjernice za izračunavanje greške metode indirektnog mjerenja možete koristiti sljedeće pravilo:

Za izračunavanje relativne greške metode indirektnog mjerenja potrebno je:

1. Odredite apsolutne greške (instrumentalne ili prosječne) direktnih mjerenja.

2. Logaritam računsku (radnu) formulu.

3. Uzimajući vrijednosti direktnih mjerenja kao nezavisne varijable, pronađite ukupni diferencijal rezultirajućeg izraza.

4. Saberite sve parcijalne diferencijale u apsolutnoj vrijednosti, zamjenjujući varijabilne diferencijale u njima odgovarajućim apsolutnim greškama direktnih mjerenja.

Na primjer, gustina cilindričnog tijela izračunava se po formuli:

(16)

Gdje m, D, h - izmjerene količine.

Dobijmo formulu za izračunavanje grešaka.

1. Na osnovu korišćene opreme utvrđujemo apsolutne greške u merenju mase, prečnika i visine cilindra (∆m, ∆D, ∆h odnosno).

2. Logaritamo izraz (16):

3. Razlikujte:

4. Zamjenom diferencijala nezavisnih varijabli apsolutnim greškama i dodavanjem modula parcijalnih inkremenata dobijamo:

5. Korištenje numeričkih vrijednosti m, D, h, D, m, h, računamo E.

6. Izračunajte apsolutnu grešku

Gdje r izračunato po formuli (16).

Predlažemo da se sami uvjerite u to u slučaju šupljeg cilindra ili cijevi unutrašnjeg prečnika D 1 i spoljni prečnik D 2

Neophodno je pribeći izračunavanju greške metode merenja (direktne ili indirektne) u slučajevima kada se višestruka merenja ili ne mogu izvršiti pod istim uslovima ili zahtevaju dosta vremena.

Ako je određivanje greške mjerenja osnovni zadatak, tada se mjerenja obično izvode više puta i izračunavaju se i aritmetička srednja greška i greška metode (greška instrumenta). Konačni rezultat ukazuje na najveće od njih.

O tačnosti proračuna

Greška u rezultatu je određena ne samo netačnostima mjerenja već i netačnostima proračuna. Proračuni se moraju izvesti tako da njihova greška bude za red veličine manja od greške u rezultatu mjerenja. Da biste to učinili, zapamtite pravila matematičkih operacija s približnim brojevima.

Rezultati mjerenja su približni brojevi. U približnom broju, svi brojevi moraju biti tačni. Posljednjom ispravnom cifrom približnog broja smatra se ona u kojoj greška ne prelazi jednu jedinicu njegove cifre. Sve cifre od 1 do 9 i 0, ako je u sredini ili na kraju broja, nazivaju se značajnim. Broj 2330 ima 4 značajne cifre, ali broj 6,1×10 2 ima samo dvije, a broj 0,0503 tri, jer su nule lijevo od 5 beznačajne. Pisanje broja 2,39 znači da su sve decimale tačne, a pisanje 1,2800 znači da su tačne i treća i četvrta decimala. Broj 1,90 ima tri značajne cifre i to znači da smo prilikom mjerenja uzeli u obzir ne samo jedinice, već i desetinke i stotinke, a broj 1,9 ima samo dvije značajne cifre i to znači da smo uzeli u obzir cijelu i desetinke i preciznost ovog broj je 10 puta manji.

Pravila za zaokruživanje brojeva

Prilikom zaokruživanja zadržavaju se samo ispravni znakovi, a ostali se odbacuju.

1. Zaokruživanje se postiže jednostavnim odbacivanjem cifara ako je prva odbačena znamenka manja od 5.

2. Ako je prva odbačena znamenka veća od 5, onda se zadnja cifra povećava za jedan. Posljednja znamenka se također povećava kada je prva cifra koja se odbacuje 5, nakon čega slijedi jedna ili više cifara koje nisu nula.

Na primjer, različita zaokruživanja od 35.856 bi bila: 35.9; 36.

3. Ako je odbačena cifra 5, a iza nje nema značajnih znamenki, onda se zaokružuje na najbliži paran broj, odnosno zadnja zadržana znamenka ostaje nepromijenjena ako je parna i povećava se za jedan ako je neparna. .

Na primjer, 0,435 je zaokruženo na 0,44; Zaokružujemo 0,365 na 0,36.

Apsolutne i relativne greške se koriste za procjenu nepreciznosti u vrlo složenim proračunima. Koriste se i u raznim mjerenjima i za zaokruživanje rezultata proračuna. Pogledajmo kako odrediti apsolutnu i relativnu grešku.

Apsolutna greška

Apsolutna greška broja nazovi razliku između ovog broja i njegove tačne vrijednosti.
Pogledajmo primjer : U školi ima 374 učenika. Ako ovaj broj zaokružimo na 400, onda je apsolutna greška mjerenja 400-374=26.

Da biste izračunali apsolutnu grešku, potrebno je da od većeg oduzmete manji broj.

Postoji formula za apsolutnu grešku. Označimo tačan broj slovom A, a slovo a - aproksimacijom tačnog broja. Približan broj je broj koji se neznatno razlikuje od tačnog i obično ga zamjenjuje u proračunima. Tada će formula izgledati ovako:

Δa=A-a. Gore smo raspravljali o tome kako pronaći apsolutnu grešku koristeći formulu.

U praksi, apsolutna greška nije dovoljna za tačnu procjenu mjerenja. Rijetko je moguće znati tačnu vrijednost mjerene veličine da bi se izračunala apsolutna greška. Mjerenje knjige dužine 20 cm i dopuštanje greške od 1 cm, može se smatrati da je mjerenje sa velikom greškom. Ali ako je napravljena greška od 1 cm pri mjerenju zida od 20 metara, ovo mjerenje se može smatrati što preciznijim. Stoga je u praksi važnije određivanje relativne greške mjerenja.

Zabilježite apsolutnu grešku broja koristeći znak ±. Na primjer , dužina rolne tapeta je 30 m ± 3 cm. Granica apsolutne greške naziva se maksimalnom apsolutnom greškom.

Relativna greška

Relativna greška Oni nazivaju odnos apsolutne greške broja i samog broja. Da bismo izračunali relativnu grešku u primjeru sa učenicima, podijelimo 26 sa 374. Dobijamo broj 0,0695, pretvorimo ga u postotak i dobijemo 6%. Relativna greška se označava kao procenat jer je bezdimenzionalna veličina. Relativna greška je tačna procjena greške mjerenja. Ako uzmemo apsolutnu grešku od 1 cm pri mjerenju dužine segmenata od 10 cm i 10 m, tada će relativne greške biti jednake 10%, odnosno 0,1%. Za segment dužine 10 cm, greška od 1 cm je vrlo velika, ovo je greška od 10%. Ali za segment od deset metara, 1 cm nije bitan, samo 0,1%.

Postoje sistematske i nasumične greške. Sistematska je greška koja ostaje nepromijenjena tokom ponovljenih mjerenja. Slučajna greška nastaje kao rezultat utjecaja vanjskih faktora na proces mjerenja i može promijeniti svoju vrijednost.

Pravila za izračunavanje grešaka

Postoji nekoliko pravila za nominalnu procjenu grešaka:

• pri sabiranju i oduzimanju brojeva potrebno je sabrati njihove apsolutne greške;
• pri dijeljenju i množenju brojeva potrebno je dodati relativne greške;
• Kada se podigne na stepen, relativna greška se množi sa eksponentom.

Približni i tačni brojevi zapisuju se pomoću decimalnih razlomaka. Uzima se samo prosječna vrijednost, jer tačna vrijednost može biti beskonačno duga. Da biste razumjeli kako napisati ove brojeve, morate naučiti o istinitim i sumnjivim brojevima.

Pravi brojevi su oni brojevi čiji rang premašuje apsolutnu grešku broja. Ako je znamenka brojke manja od apsolutne greške, naziva se sumnjiva. Na primjer , za razlomak 3,6714 sa greškom od 0,002, tačni brojevi će biti 3,6,7, a sumnjivi će biti 1 i 4. U zapisu približnog broja ostaju samo tačni brojevi. Razlomak će u ovom slučaju izgledati ovako - 3,67.

Šta smo naučili?

Apsolutne i relativne greške se koriste za procjenu tačnosti mjerenja. Apsolutna greška je razlika između tačnog i približnog broja. Relativna greška je omjer apsolutne greške broja i samog broja. U praksi se koristi relativna greška jer je tačnija.