Formula kompletne mehaničke energije fluktuiranog opružnog klatna. Besplatne oscilacije. Proljetni klatno. Proljetne definicije klatna

Definicija 1.

Besplatne oscilacije mogu se izvesti u akciji unutrašnjih sila tek nakon uklanjanja sa ravnotežnog položaja cijelog sistema.

Tako da su oscilirani izrađeni prema harmoničnom zakonu, potrebno je da sila vraća telo u ravnotežnu poziciju proporcionalna pristranosti iz ravnotežne položaja i usmjerava se na suprotnu prema raseljenju.

F (t) \u003d m a (t) \u003d - m ω 2 x (t).

Odnos sugerira da je ω frekvencija harmonične oscilacije. Ova nekretnina karakteristična je za elastičnu silu unutar primjenjivosti dungalnog zakona:

F u p \u003d - k x.

Definicija 2.

Snage bilo koje prirode koje zadovoljavaju stanje koje se zove kvazi elastičan.

Odnosno, opterećenje s masom m, koja je pričvršćena na krutost K opruga sa fiksnim krajem prikazanim na slici 2. 2. 1, sačinjavaju sistem koji može obavljati harmonične slobodne oscilacije u nedostatku sile trenja.

Definicija 3.

Teret, koji se nalazi na proljeću, naziva se linearnim harmonskim oscilatorom.

Slika 2 . 2 . 1 . Oscilacije tereta na proljeće. Nema trenja.

Kružna frekvencija

Osnova kružne frekvencije ω 0 vrši se primjenom formule drugog zakona Newton-a:

m a \u003d - k x \u003d m ω 0 2 x.

Tako da imamo:

Definicija 4.

Naziva se frekvencija ω 0 vlastita frekvencija oscilacijskog sistema.

Određivanje razdoblja harmoničnih vibracija tereta na proljeće t iz formule:

T \u003d 2 π ω 0 \u003d 2 π m k.

Horizontalna lokacija Spring-Cargo sistema, gravitacija nadoknađuje snagom reakcije podrške. Kada visete teret na proljeće, smjer gravitacije ide duž linije protoka tereta. Ravnotežni položaj rastegljenog opruga je:

x 0 \u003d m g k, dok se oscilacije izvode u blizini nove ravnotežne države. Formule vlastite frekvencije ω 0 i razdoblje oscilacije t u gornjim izrazima su fer.

Definicija 5.

Uz postojeću matematičku vezu između ubrzanja tijela A i koordinate, ponašanje oscilatornoj sustavu karakterizira strogi opis: ubrzanje je drugi izvedenik koordinate tijela X u vrijeme T:

Opis drugog zakona Newtona sa teretom na proljeće bit će evidentiran kao:

m A - m X \u003d - K X ili X ¨ + ω 0 2 x \u003d 0, gdje je besplatna frekvencija ω 0 2 \u003d k m.

Ako fizički sustavi ovise o formuli X ¨ + ω 0 2 x \u003d 0, a zatim su u stanju obavljati besplatne oscilatorne harmonske pokrete s različitim amplitudima. To je moguće jer se koristi x \u003d x m cos (ω t + φ 0).

Jednadžba obrasca x ¨ + ω 0 2 x \u003d 0 dobila ime jednadžbe besplatnih oscilacija. Njih fizička svojstva Samo vlastite frekvencije oscilacije ω ili razdoblje T.

Amplituda x M i početna faza φ 0 pronađena su korištenjem metode koja im je izvedena iz stanja ravnoteže početnog vremena.

Primjer 1.

U prisustvu raseljenog tereta iz ravnoteže ravnoteže, udaljenost Δ l i trenutak jednak t \u003d 0, smanjuje se bez početne brzine. Zatim x m \u003d Δ l, φ 0 \u003d 0. Ako je opterećenje bilo u ravnotežnoj poziciji, tada se početna brzina ± ± 0 prenosi kada se prenosi početna brzina, odavde x m \u003d m k υ 0, φ 0 \u003d ± π 2.

Amplituda x M s početnom fazom φ 0 određuje se prisutnošću početnih uvjeta.

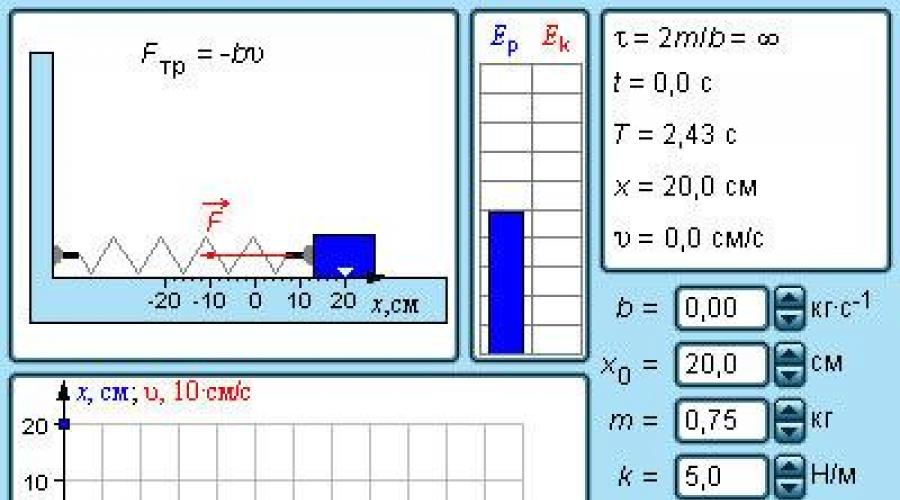
Slika 2. 2. 2. Model besplatnih inscilacija tereta na proljeće.

Mehanički oscilacijski sustavi odlikuju se prisustvom potoka elastičnih deformacija u svakom od njih. Slika 2. 2. 2 prikazuje kutni analog harmoničkog oscilatora, što čini vibracije. Disk se vodoravno vise na elastičnoj niti pričvršćenoj u svom središtu mase. Ako se rotira na kut θ, onda trenutak sile elastične deformacije uvijanja m y p p p:

M y p p \u003d - x θ.

Ovaj izraz ne odgovara zakonu grla za deformaciju zaokretanja. Vrijednost X je slična k ukočenosti proljeća. Zapisnik o Newtonovom drugom zakonu za rotacijsko kretanje diska

I ε \u003d m y p p \u003d - x θ ili θ ¨ \u003d - x θ, gdje je trenutak inercije označen od strane i \u003d i c, a ε je ugaono ubrzanje.

Slično kao i do proljetne klatno formule:

ω 0 \u003d x i, t \u003d 2 π i x.

Upotreba zatvarača za uvijanje primijeće se u mehaničkom satu. Dobio je ime balansa u kojem se stvaranje trenutnog elastičnih sila vrši pomoću spiralnog proljeća u obliku slova.

Slika 2. 2. 3. Cool Pendulum.

Ako primijetite grešku u tekstu, odaberite ga i pritisnite Ctrl + Enter

Proljetni klatno je oscilatorni sustav koji se sastoji od materijalne točke za vaganje T i opruga. Razmotrite vodoravni proljetni klatno (Sl. 1, a). To je masovno tijelo izbušeno u sredini i stavlja se na vodoravni štap, uz koji se može kliznuti bez trenja (idealan oscilatorni sistem). Štap je fiksiran između dvije vertikalne podrške.

Proljeće otporno na nevjestu pričvršćeno je na tijelo jedan kraj. Drugi kraj svog kraja utvrđen je na podršci, što je u najjednostavnijem slučaju u miru u vezi s inercijalnim referentnim sustavom, u kojem se pojavljuju oscilacije klatna. Na početku proljeća nije deformirano, a tijelo je u ravnotežnoj poziciji C. Ako se proteže ili stiskate proljeće, uklonite tijelo iz ravnoteže, tada će se pokrenuti snagu elastičnosti na strani Deformirana opruga, počet će snaga ravnoteže.

Neka stisnemo proljeće, pomeramo telo na položaj a i pustimo. Pod djelovanjem snage elastičnosti, kreće se ubrzanim. Istovremeno, maksimalna sila elastičnosti važi na tijelu, jer je najveći apsolutni izduženje x m opruga. Shodno tome, u ovom položaju maksimalno ubrzanje. Kada se tijelo pomiče na položaj ravnoteže, apsolutno produženje proljeća smanjuje se, a samim tim, ubrzanje se smanjuje, izviještena elastičnošću silom. Ali pošto je ubrzanje na ovom pokretu obloženo brzinom, brzina klatna povećava i u ravnotežnoj poziciji to će biti maksimalno.

Nakon što je dostigao položaj ravnoteže C, tijelo se neće zaustaviti (iako proljeće nije deformirano u ovom položaju, a jačina elastičnosti je nula), a brzina će se preći na inerciju, istezanje proljeća. Snaga elastičnosti u nastajanju sada je usmjerena protiv pokreta tijela i usporava se. U točki d, tjelesna brzina će biti nula, a ubrzanje je maksimalno, tijelo će se na trenutak zaustaviti, nakon čega će se elastičnost početi kretati u suprotnom smjeru, na mjesto ravnoteže. On ga nunite inercija, telo, stiskajući proljeće i usporavanje pokreta, dostiže tačku A (budući da nema trenja), tj. Kompletna puna oscilacija. Nakon toga kretanje tijela bit će ponovljeno u opisanom nizu. Dakle, razlozi za slobodne oscilacije proljetnog klatna su učinak sile elastičnosti koji proizlaze tokom deformacije proljeća i inertnost tijela.

Prema zakonu grla f x \u003d -kx. Prema Drugom zakonu Newton F X \u003d MA X. Slijedom toga, ma x \u003d -kx. Odavde

Dinamična jednadžba pokreta Spring Pendulum.

Vidimo da se ubrzanje direktno kreće, a suprotno usmjereno. Upoređujući dobivenu jednadžbu sa harmoničnom ekvivacijom oscilacija Vidimo da proljetni klatno vrši harmonične oscilacije s cikličnom frekvencijom

Period oscilacija proljetnog klatna.

U istoj formuli može se izračunati razdoblje oscilacija vertikalnog opružnog klatna (Sl. 1. B). Zaista, u ravnotežnom položaju, zbog delovanja gravitacije, proljeće se već proteže na određenu vrijednost x 0, određene omjerom Mg \u003d KX 0. Kada klatna prikazuje ravnotežnu poziciju o X projekciji sile elastičnosti

Ako pomaknete loptu sa ravnotežnog položaja na udaljenosti x, tada će proširenje opruge postati jednako Δl 0 + x. Tada će rezultirajuća sila uzeti vrijednost:

S obzirom na stanje ravnoteže (1.7.1), dobivamo:

Znak "minus" pokazuje da pomak i moć imaju suprotne smjerove.

Elastična snaga F ima sljedeća svojstva:

1. Proporcionalan je raseljavanju lopte iz ravnoteže;
2. Uvijek je usmjeren prema položaju ravnoteže.

Da biste obavijestili sistem za pomak X, morate obaviti posao protiv elastične snage:

Ovaj rad odlazi na stvaranje zaliha potencijalnog energetskog sistema:

Pod djelovanjem elastične snage, lopta će se preseliti na položaj ravnoteže sa sve većem brzinom. Stoga će potencijalna energija sistema smanjiti, ali kinetička energija se povećava (vaganje zanemarivanja opruga). Dođite na ravnotežni položaj, lopta će se inercijatirati inercija. Ovo je usporeno kretanje i zaustavlja se kada kinetička energija potpuno prelazi u potencijal. Tada će isti postupak teći kada se lopta kreće u suprotnom smjeru. Ako u sustavu nema trenja, lopta će dugo fluktuirati.

Jednadžba drugog zakona Newtona u ovom slučaju ima oblik:

Transformiramo jednadžba poput ovog:

Unos oznake, dobivamo linearnu homogenu diferencijalnu jednadžbu drugog reda:

Direktna zamjena je lako osigurati da opće rješenje jednadžbe (1.7.8) ima obrazac:

ako je amplituda i φ - početna faza oscilacija - trajne vrijednosti. Shodno tome, fluktuacija proljetnog klatna je skladna (Sl. 1.7.2).

Sl. 1.7.2. Harmonična oscilacija

Zbog periodičnosti kosinua, razne države oscilatorno sustava ponavljaju se nakon određenog vremenskog perioda (razdoblje oscilacija) t, za koji faza oscilacije prima prirast 2π. Izračunajte razdoblje pomoću ravnopravnosti:

odakle slijedi:

Broj oscilacija po jedinici vremena naziva se frekvencija:

Učestalost takvog oscilacije uzima se po jedinici frekvencije, od kojih je period od kojih je 1 s. Takva se jedinica zove 1 Hz.

Od (1.7.11) slijedi da:

Shodno tome, ω 0 je broj oscilacija izvedenih u 2π sekundi. Vrijednost ω 0 naziva se kružna ili ciklička frekvencija. Korištenje (1.7.12) i (1.7.13), napišite:

Diferenciranje () na vrijeme, dobivamo brzinu brzine lopte:

Od (1.7.15) slijedi da se brzina također mijenja harmoničnim zakonom i ispred promjene u fazi ½π. Razlikovanje (1.7.15), dobivamo ubrzanje:

1.7.2. Matematički klatno

Matematički klatno Oni nazivaju idealizirani sustav koji se sastoji od nesezonske težine bez težine, na kojem se tijelo suspendira, čija je cijela masa koncentrirana u jednom trenutku.

Odstupanje klatna na ravnotežnom položaju karakterizira ugao φ formiran navoj sa okomitom (Sl. 1.7.3).

Sl. 1.7.3. Matematički klatno

Uz odstupanje klatna iz ravnotežnog položaja nastaje rotacijski trenutak koji nastoji vratiti klatno na ravnotežni položaj:

Napisat ćemo za klatno jednadžbu dinamike rotacijskog pokreta, s obzirom na to da je trenutak njegove inercije ML 2:

Ova jednadžba može uzrokovati:

Ograničeno na slučaj malih oscilacija Sinφ ≈ φ i uvođenje imenovanja:

jednadžba (1.7.19) može biti predstavljena na sljedeći način:

Što se poklapa u obliku s jednadžbom fluktuacija u proljetnom klatnom. Shodno tome, njegovo rješenje će biti harmonična oscilacija:

Od (1.7.20) slijedi da ciklična frekvencija oscilacija matematičkog klatna ovisi o njegovoj dužini i ubrzanju slobodnog pada. Korištenje formule za razdoblje oscilacije () i (1.7.20), dobivamo poznat omjer:

1.7.3. Fizički klatno

Naziva se fizički klatno čvrstSposoban je izvesti oscilacije oko fiksne točke koja se ne podudara sa centrom inercije. U ravnotežnom položaju inercija klatna u klatno je pod ustima ovjesa na jednoj okomitu s njom (Sl. 1.7.4).

Sl. 1.7.4. Fizički klatno

Kada je klatna odstupila iz ravnoteže u ugao φ, nastaje rotacijski trenutak koji nastoji vratiti klatno na ravnotežni položaj:

gdje je m masa klatna, l je udaljenost između tačke ovjesa i inercijskog centra klatna.

Pisat ćemo na klatno jednadžbu dinamike rotacijskog pokreta, s obzirom na to da je trenutak njegove inercije jednak I:

Za male oscilacije sinφ ≈ φ. Zatim uvođenje oznake:

koji se takođe poklapa sa obrascem s jednadžbom fluktuacija u proljetnom klatnom. Iz jednadžbi (1.7.27) i (1.7.26) Slijedi da sa malim odstupanjima fizičkog klatna iz ravnoteže, čini harmoničnu oscilaciju, čija učestalost ovisi o masi menduluma, trenutka inercije i Udaljenost između osi rotacije i centra inercije. Sa (1.7.26) možete izračunati razdoblje oscilacija:

Upoređivanje formula (1.7.28) i () Dobijamo taj matematički klatno sa dužinom:

bit će isti period oscilacija kao što se razmatra fizički klatno. Iznos (1.7.29) se zove dat dužina Fizički klatno. Slijedom toga, dužina fizičkog klatna je dužina takvog matematičkog klatna, čiji je period oscilacija jednakim razdoblju oscilacija ovog fizičkog klatna.

Point na ravnoj liniji koja povezuje tačku ovjesa s centrom inercije, koji leži na udaljenosti dužine dužine od osi rotacije, naziva se centar za ljuljanje Fizički klatno. Na Steiner Theorem, trenutak inercije fizičkog klatna je:

gdje sam 0 trenutak inercije u odnosu na centar inercije. Zamjena (1.7.30) u (1.7.29), dobivamo:

Stoga je dužina duljine uvijek veća od udaljenosti između tačke ovjesa i inercijskog centra klatna, tako da se tačka ovjesa i ljuljački centar leže na različitim stranama iz centra inercije.

1.7.4. Energija harmoničnih oscilacija

U harmoničnoj oscilaciji, periodično međusobno pretvorljivost kinetičke energije fluktuiranog tijela i potencijalne energije E p, zbog djelovanja kvazi-elastične sile. Od ovih energija, ukupna energija e-e za oscilatorni sistem je sastavljena:

Podižemo posljednji izraz

Ali k \u003d mω 2, pa dobijamo izraz za ukupnu energiju osciliranog tijela

Dakle, ukupna energija harmonične oscilacije je konstantna i proporcionalna je kvadratu amplitude i kvadrata kružne frekvencije oscilacije.

1.7.5. Tekuće oscilacije .

Prilikom proučavanja harmonične oscilacije, trenje i otporne snage nisu uzete u obzir koji postoje u stvarnim sistemima. Radnja ovih snaga značajno mijenja prirodu pokreta, oscilacija postaje pokušaj.

Ako sustav osim sile otpornosti (trenje sile), drugi zakon Newtonove djela u sustavu, tada se newtonov drugi zakon može napisati na sljedeći način:

gdje je r trenjeni koeficijent karakterizira svojstva srednjeg za kretanje. Zamjena (1.7.34B) u (1.7.34A):

Grafikon ove funkcije prikazan je na slici.1.7.5 solidne krivulje 1, a moždana linija 2 prikazuje promjenu amplitude:

Sa vrlo malim trenjem, period propadajuće oscilacije u blizini je razdoblje oscilacije bez fluida (1.7.35.b)

Određuje se brzina opada amplitude oscilacija koeficijent prigušenja: Veći β, jači inhibitni učinak srednjeg i brže amplitude opada. U praksi, stepen prigušivanja često karakterizira logaritamsko smanjenje prigušenjaRazumijevanje ovog iznosa jednak prirodnom logaritamu odnosa dvije uzastopne amplitude oscilacija, odvojeni vremenski interval jednak periodu oscilacija:

;

Shodno tome, koeficijent prigušenja i logaritamski skranje prigušivanja su prilično jednostavna ovisnost:

S snagom prigušivanjem formule (1.7.37) može se vidjeti da je razdoblje oscilacije imaginarna vrijednost. Pokret u ovom slučaju se već naziva aperiodik. Grafikon aperiodalnog pokreta u obliku prikazan je na Sl. 1.7.6. Nazivaju se nesrećne i blede oscilacije vlastiti ili slobodan. Oni nastaju zbog početnog zapremina ili početne brzine i obavljaju se u nepostojanju vanjskog utjecaja zbog prvobitno akumulirane energije.

1.7.6. Prisilne oscilacije. Rezonanca .

Prisiljen fluktuacije se nazivaju onima koji se javljaju u sistemu sa sudjelovanjem vanjske sile koja se razlikuju u periodičnom zakonu.

Pretpostavimo da sila koja stvara vanjske sile djeluje na materijalnu točku pored kvazi elastične sile

,

gdje je f 0 amplituda; ω - kružna frekvencija fluktuacija sile prisiljavanja. Napravite diferencijalnu jednadžbu (Newtonov drugi zakon):

,

Amplituda prisilnog oscilacije (1.7.39) izravno je proporcionalna amplitudi generacije i ima složenu ovisnost o koeficijentu prigušenja srednje i kružnih frekvencija vlastite i prisilne oscilacije. Ako se daju ω i β za sustav, amplituda prisilnih oscilacija ima maksimalnu vrijednost na određenoj određenoj frekvenciji prisiljavanja, nazvanim rezonantan.

Sam fenomen - navedeno postizanje maksimalne amplitude za ω i β i β - rezonanca.

Sl. 1.7.7. Rezonanca

U nedostatku otpora na amplitudu prisilnih oscilacija tokom rezonancije beskonačno je velika. U ovom slučaju, od ω \u003d ω 0, i.e. Rezonanca u sistemu bez prigušenja događa se kada se učestalost prisilne sile poklapa sa učestalošću vlastitih oscilacija. Grafička ovisnost amplitude prisilnih oscilacija iz kružne frekvencije prisilne sile u različitim vrijednostima koeficijenta prigušivanja prikazana je na slici. pet.

Mehanička rezonanca može biti i korisni i štetni fenomen. Štetni učinak rezonancije uglavnom je zbog uništenja koji može izazvati. Dakle, u tehnici s obzirom na različite vibracije, potrebno je osigurati moguću pojavu rezonantnih uvjeta, u protivnom mogu biti uništavanje i katastrofe. Tijela obično imaju nekoliko oscilacijskih frekvencija i, u skladu s tim, nekoliko rezonantnih frekvencija.

Ako ne bi bio koeficijent prigušivanja unutrašnjih organa, tada rezonantni pojave koji su nastali u ovim organima pod utjecajem vanjskih vibracija ili zvučnih talasa mogla dovesti do tragičnih posljedica: oštećenje ligamenata, itd . Međutim, takve pojave u umjerenim vanjskim utjecajima praktično se primijećuje, jer je koeficijent prigušenja bioloških sistema prilično velik. Ipak, rezonantne pojave pod djelovanjem vanjskih mehaničkih oscilacija nastaje u unutrašnjim organima. U ovome, očigledno, jedan od razloga negativnih efekata infroode fluktuacija i vibracija na ljudskom tijelu.

1.7.7. Autocalbania

Postoje i takvi oscilacijski sustavi koji sami reguliraju periodično nadopunjavanje energije imanja i zato može dugo fluktuirati.

Nazivaju se prometne fluktuacije koje postoje u bilo kojem sistemu u nedostatku naizmjeničnog vanjskog utjecaja samostalnii sami sustav - samooscilacioni.

Amplituda i učestalost samoinscilacija ovise o svojstvima u najugroženijem autokalibularnim sistemu, za razliku od prisilnih oscilacija, oni nisu određeni vanjskim utjecajima.

U mnogim slučajevima samozascilirajuće sisteme mogu predstavljati tri glavna elementa (Sl.1.7.8): 1) stvarni oscilirajući sistem; 2) izvor energije; 3) Regulator protoka energije u samom vibracijskom sistemu. Kanal oscilatorni sistem povratne informacije (Sl. 6) utiče na regulator, informišući regulator o stanju ovog sistema.

Klasični primjer mehaničkog auto-oscilatornog sustava je sat u kojem su klatno ili ravnoteža oscilacijski sustav, proljeće ili podignuta Gyry - izvor energije, a sidro je regulator protoka energije iz izvora u oscilatorni sistem.

Mnogi biološki sustavi (srce, plući, itd.) Su samostalni. Karakterističan primjer elektromagnetskog auto-osciliranog sistema je generatori samoinscilacija.

1.7.8. Dodavanje oscilacija jednog smjera

Razmotrite dodavanje dvije harmonske oscilacije istog smjera i iste frekvencije:

x 1 \u003d A 1 CO (ω 0 T + Α 1), x 2 \u003d A 2 CO (ω 0 T + Α 2).

Harmonična oscilacija može se postaviti pomoću vektora čija je dužina jednaka amplitudi oscilacija, a smjer čini ugao s nekom osovinom jednakom početnom fazom oscilacija. Ako se ovaj vektor rotira s kutnom brzinom ω 0, tada će se njegova projekcija na odabranoj osi promijeniti harmoničnim zakonom. Na osnovu toga biramo neke osi x i zamislimo oscilacije pomoću vektora A 1 i A 2 (Sl.1.7.9).

Sa slike.1.7.6 To slijedi to

.

Sheme u kojima su oscilacije prikazane grafički u obliku vektora u ravnini nazivaju se vektorskim dijagramima.

Od formule 1.7.40 slijedi. Što ako je fazna razlika obje oscilacije jednake nuli, amplituda rezultirajuće oscilacije jednaka je zbroju amplitude sklopivih oscilacija. Ako je razlika u fazama sklopivih oscilacija jednaka, tada je amplituda rezultirajuće oscilacije jednaka. Ako frekvencije izračunatih oscilacija nisu iste, tada će vektori koji odgovaraju tim fluktuacijama rotirat će različita brzina. U ovom slučaju, rezultirajući vektor pulsira u veličini i rotira se sa trajnom brzinom. Shodno tome, kao rezultat dodatka, on ne pokazuje da nije harmonična oscilacija, već složen oscilatorni proces.

1.7.9. Biivia

Razmotrite dodavanje dvije harmonične oscilacije istog smjera koji se razlikuju u frekvenciji. Pustite učestalost jednog od njih jednaka ω, a druga ω + δω i Δω<<ω. Положим, что амплитуды складываемых колебаний одинаковы и начальные фазы обоих колебаний равны нулю. Тогда уравнения колебаний запишутся следующим образом:

x 1 \u003d A cos ωt, x 2 \u003d A cos (ω + δω) t.

Nakon kreiranja ovih izraza i korištenjem formule za količinu kosinua, dobivamo:

Oscilacije (1.7.41) mogu se smatrati harmoničnom oscilacijom frekvencije ω, a amplituda čije promjene zakonom. Ova je funkcija periodična s frekvencijom dva puta veća od frekvencije izraza pod znakom modula, I.E. Sa frekvencijom Δω. Stoga je frekvencija amplitudno pulsacija, nazvana frekvencija otkucaja, jednaka razlikovanju u frekvenciji sklopivih oscilacija.

1.7.10. Dodavanje međusobno okominskih oscilacija (figure lissuzh)

Ako materijalna tačka izvrši oscilacije i duž osi X i duž osi y, tada će se kretati duž neke krivilogradske putanje. Neka učestalost oscilacija iste i početne faze prve oscilacije jednako nuli, tada će u obrascu napisati jednadžbe oscilacije:

Jednadžba (1.7.43) Jednadžba ellipse, a osovine su orijentirane proizvoljno u odnosu na koordinatne osi x i y. Orijentacija elipse i veličine svojih poluoseka ovisi o amplitudi A i B i faznoj razlici α. Razmotrite neke određene slučajeve:

Ovo je jednadžba ellipse, od kojih se osi poklapaju sa osi koordinata, a njegove poluoseke su jednake amplitudi (Sl. 1.7.12). Ako su amplitude jednake, elipse postaje krug.

Sl.1.7.12

Ako se frekvencije međusobno okomita oscilacija razlikuju po niskoj vrijednosti Δω, mogu se smatrati oscilacija iste frekvencije, ali s polako promjenom fazne razlike. U ovom slučaju mogu se zabilježiti jednadžbe oscilacije

x \u003d A cos ωt, y \u003d b cos [ωt + (Δωt + α)]

a izraz Δωt + α smatra se fazom razlike, polako se mijenjajući s vremenom prema linearnom zakonu. Rezultirajući pokret u ovom slučaju javlja se duž sporo mijenjane krivulje, što će dosljedno uzeti oblik koji ispunjava sve vrijednosti fazne razlike od -π do + π.

Ako frekvencije međusobno okominskih oscilacija nisu iste, putanje nastalog pokreta ima izgled prilično složenih krivulja, nazvanih figure Lissen. Ostavite, na primjer, frekvencije preklopljenih oscilacija pripadaju kao 1 : 2 i fazna razlika π / 2. Tada su jednadžbe oscilacije

x \u003d A cos ωt, y \u003d b cos.

Tokom vremena dok se po osi x, tačka se kreće iz jedne ekstremne pozicije na drugu, duž osi y, izlazi iz nulte pozicije, ima vremena za postizanje jednog ekstremnog položaja, a zatim drugi i povratak. Pogled na krivulju prikazan je na slici. 1.7.13. Krivulja sa istim omjerom frekvencije, ali fazna razlika je nula prikazana na slici.1.7.14. Omjer frekvencija izračunatih oscilacija Potražite omjer broja točaka sjecišta figura, lissing s ravnim, paralelnim osovinama koordinata. Stoga, prema obliku figure Lissuzh, možete odrediti omjer frekvencija sklopivih oscilacija ili nepoznate frekvencije. Ako je poznata jedna od frekvencija.

Sl.1.7.13

Sl.1.7.14

Što je bliže jedinici racionalna frakcija koja izražava frekvencijsku frekvenciju oscilacija, teže su figure laživanja.

1.7.11. Distribucija talasa u elastičnom okruženju

Ako u bilo kojem mjestu elastična (čvrsta tekućina ili plinovito) medij za pokretanje oscilacija svojih čestica, zatim zbog interakcije čestica, ova oscilacija će se distribuirati u okruženju od čestice do čestice na neku brzinu. Podat će se proces distribucije oscilacija u prostoru val.

Srednje čestice u kojima val primjenjuje nije uključen u talas u translacijskom pokretu, oni čine samo oscilacije u blizini svojih ravnotežnih odredbi.

Ovisno o područjima oscilacija česticama u odnosu na smjer u kojem se val distribuira, razlikuje se longitudinal I. poprečan Valovi. U uzdužnom valu, čestica srednja fluktuira u širenju vala. U poprečnom valu, srednje čestice fluktuira u pravcima okomito na smjer širenja valova. Elastični poprečni valovi mogu se pojaviti samo u mediju s smicanjem otporom. Stoga je u tekućim i gasovitim medijima moguće nastaviti samo uzdužne valove. U čvrstom mediju mogu se pojaviti oba uzdužne i poprečne valove.

Na slici. 1.7.12 prikazuje kretanje čestica kada se distribuira u poprečnom valnom medijumu. Sobe su 1.2, itd. Čestice se međusobno zaostaju za daljinu jednaku (¼t), tj. Na udaljenosti pređenom valom na četvrtinu razdoblja oscilacija koje izvode čestice. Tada je vrijeme potrebno za nulu, val, širenje duž osi s lijeva na desno, doseglo je česticu 1, kao rezultat čega je čestica počela prelaziti sa stajališta ravnoteže prema gore, fascinantne sljedeće čestice. Četvrtina razdoblja čestica 1 dostiže ekstremni gornji položaj ravnoteže čestica 2. Na dolasku još jednog tromjesečja, prvi dio će biti položaj ravnoteže, kretanja u smjeru od vrha do dna, Druga čestica će dostići ekstremnu gornju poziciju, a treća čestica će početi premjestiti ravnotežnu poziciju. U trenutku vremena jednako t, prva čestica će završiti puni ciklus oscilacija i bit će u istom stanju pokreta kao pojašnjenje. Val do vremena T, koji je prošao stazu (υt), stići će do čestica 5.

Na slici. 1.7.13 prikazuje kretanje čestica kada se uzdužni val distribuira u mediju. Sve obrazloženje u vezi s ponašanjem čestica u poprečnom valu mogu se pripisati i u ovom slučaju s zamjenom pomaka gore-dolje po odstupaju s desne strane i lijevo.

Sa cifre je jasno da se kada se propagiraju uzdužni val, naizmjenične koncentracije i pražnjenje čestica (mjesto koncentracije je zaokruženo u liniji figura), kreće se u smjeru širenja valnog širenja na brzini.

Sl. 1.7.15

Sl. 1.7.16

Na slici. 1.7.15 i 1.7.16 prikazuju oscilacije čestica, poziciju, čija ravnoteža leži na osovini x.U stvari, ne samo čestice koji se ne smiju fluktuirati u osovini xi ukupnost čestica zaključena u nekom volumenu. Širenje iz izvora oscilacija, valni proces pokriva sve nove i nove dijelove prostora, geometrijsku lokaciju bodova, na koje oscilacije dostižu trenutak t, nazvali prednji dio talasa (ili naslovni val). Front Wave predstavlja površinu koja razdvaja dio prostora koji je već uključen u talasni proces, od područja u kojem se oscilacije još nisu nastale.

Pozva se geometrijska lokacija točaka, fluktuiranje u istoj fazi talasna površina . Valna površina može se izvesti kroz bilo koju točku prostora prekrivenog postupkom talasa. Stoga valne površine nalazi se beskonačni set, dok je val ispred svaki put samo jedan. Valne površine ostaju neviđevi (prolaze kroz položaj ravnoteže čestica, fluktuiraju u jednoj fazi ). Wavefront se stalno kreće.

Valne površine mogu biti bilo koji oblik. U najjednostavnijim slučajevima imaju oblik aviona ili sfere. U skladu s tim, talas u tim slučajevima naziva se ravno ili sferno. U ravnom talasu valne površine su postavljeni paralelni sa jednim avionima, u sfernom valu - mnoštvo koncentričnih sfera.

Sl. 1.7.17

Pustite da se ravni val širi duž osi x.. Tada sve tačke sfere, položaj, čiji ravnoteža ima istu koordinatu x.(ali razlika koordinatnih vrijednosti y.i z)fluktuirajte u istoj fazi.

Na slici. 1.7.17 prikazuje krivulju koja daje odstupanje ξ sa položaja ravnotežnih bodova s \u200b\u200brazličitim x.u nekom trenutku. Ovaj obrazac ne biste trebali uočiti kao vidljiva slika vala. Na slici prikazan raspored funkcija. ξ (x, T)za neke fiksne vremenski trenutak t.Takav raspored može se izgraditi i za uzdužnu i za poprečni val.

Udaljenost λ, talas se širi kratko vrijeme, jednak periodu oscilacija čestica srednjeg, naziva se talasna dužina. Očigledno je da

gdje je brzina talasa, t- period oscilacija. Walrow Dužina dužine kao i udaljenost između najbližih mjesta srednjeg, fluktuirajući faznu razliku, jednak 2π (vidi Sl. 1.7.14)

Zamjena u omjeru (1.7.45) T do 1 / ν (ν - frekvencija oscilacija), dobivamo

Ova formula može doći i iz sljedećih razmatranja. U jednoj sekundi, izvor talasa obavlja ν oscilacije, generirajući u mediju sa svakim oscilacijama jedan "češalj" i jedan "val" valove. Do trenutka kada se izvor završi ν - E fluktuacije, prvi "češalj" imat će vremena za prenos staze. Slijedom toga, "grebeni" i "vPadin" valovi moraju biti ispunjeni u dužini υ.

1.7.12. Jednadžba ravne valove

Valna jednadžba naziva se izraz koji premještanje oscilirajuće čestice daje kao funkciju svojih koordinata x, y, z i vrijeme t. :

ξ \u003d ξ (x, y, z; t)

(Imaju u vidu koordinate ravnotežnog položaja čestica). Ova značajka mora biti periodična o vremenu t. i u odnosu na koordinate x, y, z. . Periodičnost u vremenu slijedi iz činjenice da su točke koje su odvojene jedna od druge na daljinu λ , fluktuiraju na isti način.

Pronađite oblik funkcije ξ u slučaju ravnog vala, pretpostavljajući da su oscilacije skladne. Da biste pojednostavili, pošaljite osovinu koordinata tako da se osovina x. poklopilo se sa smjerom širenja valova. Tada će talasne površine biti okomito na osovinu x. i, budući da su sve tačke talasnog površinskog raspona jednako, offset ξ ovisit će samo o x. i t.:

ξ = ξ (x, t) .

Sl.1.7.18

Neka oscilacije tačaka leže u avionu x. = 0 (Sl. 1.7.18), jesu

Pronađite vrstu oscilacije bodova u ravnini koji odgovara proizvoljnoj vrijednosti x. . Kako bi se putanje proslijedio iz aviona X.=0 prije ovog aviona val treba vremena ( υ - Accpair širenja talasa). Shodno tome, oscilacije čestica leže u avionu x. zaostaje na vreme τ Od oscilacija čestica u avionu x. = 0 . Će se pojaviti

Dakle, jednadžba ravne valove (uzdužno i poprečno), širenje u smjeru osi x. , kao što slijedi:

Ovaj izraz određuje odnos između t i mjesto x. u kojoj faza ima fiksnu vrijednost. Rezultat DX / DT vrijednost daje brzinu kojom se ova fazna vrijednost kreće. Ogorčeno izražavanje (1.7.48), dobivamo

Jednadžba vala koja se širi prema silaznici x. :

U zaključku formule (1.7.53), pretpostavili smo da amplituda oscilacija ne ovisi x. . Za ravan val, to se uočava u slučaju kada valna energija ne apsorbira medij. Kada se distribuira u apsorpciji energije, intenzitet vala s uklanjanjem iz izvora oscilacija se postepeno smanjuje - val je prigušivanje. Iskustvo pokazuje da se u homogenom medijumu takvo prigušenje događa u eksponencijalnom zakonu:

Respektivno ravna valna jednadžba, uzimajući u obzir prigušenjeIma sljedeći obrazac:

(A 0 - amplituda na tačkima aviona x \u003d 0).