Kako napraviti analitički model linearne funkcije. Proučavanje linearne funkcije. Zaštita ličnih podataka
Očuvanje vaše privatnosti nam je važno. Iz tog razloga smo razvili Politiku privatnosti koja opisuje kako koristimo i pohranjujemo vaše podatke. Pregledajte našu praksu privatnosti i javite nam ako imate pitanja.
Prikupljanje i korištenje ličnih podataka
Lični podaci odnose se na podatke koji se mogu koristiti za identifikaciju ili kontaktiranje određene osobe.
Od vas se može tražiti da unesete svoje lične podatke u bilo koje vrijeme kada nas kontaktirate.
U nastavku su navedeni neki primjeri vrsta ličnih podataka koje možemo prikupljati i kako ih možemo koristiti.
Koje lične podatke prikupljamo:
- Kada podnesete prijavu na stranici, možemo prikupljati različite informacije, uključujući vaše ime, broj telefona, adresu e-pošte itd.
Kako koristimo vaše lične podatke:
- Lični podaci koje prikupljamo omogućavaju nam da vas kontaktiramo s jedinstvenim ponudama, promocijama i drugim događajima i nadolazećim događajima.
- S vremena na vrijeme možemo koristiti vaše lične podatke za slanje važnih obavijesti i komunikacija.
- Lične podatke možemo koristiti i za interne svrhe, kao što su provođenje revizija, analiza podataka i različita istraživanja kako bismo poboljšali usluge koje pružamo i dali vam preporuke u vezi s našim uslugama.
- Ako učestvujete u nagradnoj igri, natjecanju ili sličnoj promociji, možemo koristiti informacije koje nam date za upravljanje takvim programima.
Otkrivanje informacija trećim licima
Podatke koje dobijemo od vas ne otkrivamo trećim licima.
Izuzeci:
- Ako je potrebno - u skladu sa zakonom, sudskim postupkom, u sudskom postupku, i/ili na osnovu javnih zahtjeva ili zahtjeva državnih organa u Ruskoj Federaciji - otkriti vaše lične podatke. Takođe možemo otkriti informacije o vama ako utvrdimo da je takvo otkrivanje neophodno ili prikladno za sigurnosne, provođenje zakona ili druge svrhe od javnog značaja.
- U slučaju reorganizacije, spajanja ili prodaje, možemo prenijeti lične podatke koje prikupimo na odgovarajuću treću stranu.
Zaštita ličnih podataka
Poduzimamo mjere opreza - uključujući administrativne, tehničke i fizičke - da zaštitimo vaše osobne podatke od gubitka, krađe i zloupotrebe, kao i neovlaštenog pristupa, otkrivanja, izmjene i uništenja.
Poštivanje vaše privatnosti na nivou kompanije
Kako bismo osigurali da su vaši lični podaci sigurni, našim zaposlenima prenosimo standarde privatnosti i sigurnosti i striktno provodimo praksu privatnosti.
Sažmite i sistematizirati znanja na temu “Linearna funkcija”:
- konsolidovati sposobnost čitanja i građenja grafova funkcija datih formulama y = kx+b, y = kx;
- konsolidovati sposobnost određivanja relativnog položaja grafova linearnih funkcija;
- razviti vještine rada sa grafovima linearnih funkcija.
Develop sposobnost analiziranja, poređenja, izvođenja zaključaka. Razvijanje kognitivnog interesovanja za matematiku, kompetentan usmeni matematički govor, tačnost i preciznost u konstrukciji.
Vaspitanje pazljivost, samostalnost u radu, sposobnost rada u paru.
Oprema: ravnalo, olovka, kartice sa zadacima, olovke u boji.
Vrsta lekcije: lekcija o konsolidaciji naučenog materijala.
Plan lekcije:
- Organiziranje vremena.
- Usmeni rad. Matematički diktat sa samotestiranjem i samoprocjenom. Istorijski izlet.
- Vježbe treninga.
- Samostalan rad.
- Sažetak lekcije.
- Zadaća.
Tokom nastave
1. Navedite svrhu lekcije.
Svrha časa je sumiranje i sistematizacija znanja na temu „Linearna funkcija“.
2. Počnimo s provjerom vašeg teorijskog znanja.
– Definirajte funkciju. Šta je nezavisna varijabla? Zavisna varijabla?
– Definirajte graf funkcije.
– Formulirajte definiciju linearne funkcije.
– Šta je graf linearne funkcije?
– Kako grafički prikazati linearnu funkciju?
– Formulisati definiciju direktne proporcionalnosti. Šta je graf? Kako napraviti grafikon? Kako se graf funkcije y = kx nalazi u koordinatnoj ravni za k > 0 i za k< 0?
Matematički diktat sa samotestiranjem i samoprocjenom.
Pogledaj slike i odgovori na pitanja.
1) Graf koje funkcije je suvišan?
2) Koja slika prikazuje grafik direktne proporcionalnosti?
3) Na kojoj slici grafik linearne funkcije ima negativan nagib?
4) Odredi predznak broja b. (Napiši odgovor kao nejednakost)
Provjera rada. Ocjena.
Raditi u parovima.
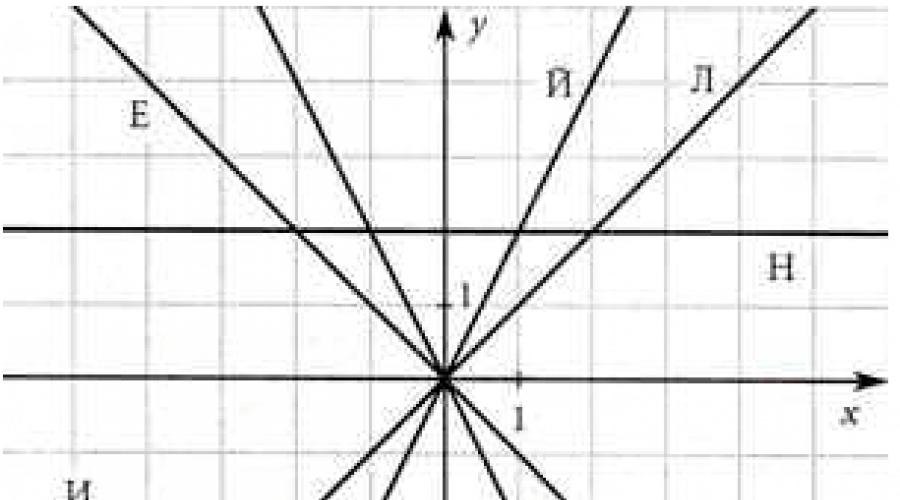
Dešifrirajte ime matematičara koji je prvi upotrijebio izraz funkcija. Da biste to učinili, upišite u okvire slovo koje odgovara grafikonu date funkcije. Upiši slovo C u preostali kvadrat Dopuni crtež grafikom funkcije koja odgovara ovom slovu.

Slika 1

Slika 2

Slika 3
Gottfried Wilhelm Leibniz, 1646-1716, njemački filozof, matematičar, fizičar i lingvista. On i engleski naučnik I. Newton stvorili su (nezavisno jedan od drugog) temelje važne grane matematike – matematičke analize. Leibniz je uveo mnoge koncepte i simbole koji se i danas koriste u matematici.
3. 1. Date su funkcije specificirane formulama: y = x-5; y = 0,5x; y = – 2x; y = 4.
Imenujte funkcije. Navedite grafove koja od ovih funkcija prolazi kroz tačku M (8;4). Šematski pokažite kako će izgledati crtež ako na njemu prikažete grafove funkcija koje prolaze kroz tačku M.

2. Graf direktne proporcionalnosti prolazi kroz tačku C (2;1). Kreirajte formulu koja specificira direktnu proporcionalnost. Pri kojoj vrijednosti m će graf proći kroz tačku B (-4;m).
3. Grafikujte funkciju datu sa y=1/2X. Kako možete iz grafa date funkcije dobiti grafik funkcije date formulom y=1/2X – 4 i y = 1/2X+3. Analizirajte dobijene grafikone.
4. Funkcije su date formulama:
1) y= 4x+9 i y= 6x-5;
2) y=1/2x-3 i y=0,5x+2;
3) y= x i y= -5x+2,4;
4) y= 3x+6 i y= -2,5x+6.
Koji je relativni položaj grafova funkcija? Bez izvođenja bilo kakve konstrukcije, pronađite koordinate presječne točke prvog para grafova. (samotestiranje)
4. Samostalni rad u parovima. (izvedeno na ml papiru). Interdisciplinarna komunikacija.
Potrebno je konstruirati grafove funkcija i odabrati onaj njegov dio za tačke za koje vrijedi odgovarajuća nejednakost:
y = x + 6, 4 < X < 6; y = -x + 6, -6 < X < -4; y = – 1/3 x + 10, -6 < X < -3; y = 1/3 x +10, 3 < X < 6; y = -x + 14, 0 < X < 3; y = x + 14, -3 < X < 0; y = 9x – 18, 2 < X < 4; y = – 9x – 18 -4 < X < -2; y = 0, -2 < X < 2.
Kakav si crtež dobio? ( Tulip.)

Malo o tulipanima:
Poznato je oko 120 vrsta tulipana, rasprostranjenih uglavnom u srednjoj, istočnoj i južnoj Aziji i južnoj Evropi. Botaničari veruju da je kultura tulipana nastala u Turskoj u 12. veku. Svetsku slavu biljka je stekla daleko od svoje domovine, u Holandiji, s pravom nazvana Zemlja lala.
Evo legende o tulipanu. Sreća je bila sadržana u zlatnom pupoljku žutog tulipana. Do ove sreće niko nije mogao doći, jer nije bilo te sile koja bi mogla otvoriti svoj pupoljak. Ali jednog dana jedna žena sa djetetom šetala je livadom. Dječak je pobjegao iz majčinog zagrljaja, dotrčao do cvijeta uz zvonki smijeh, a zlatni pupoljak se otvorio. Bezbrižni dječiji smeh postigao je ono što nijedna sila nije mogla. Od tada je postao običaj da se tulipani poklanjaju samo onima koji osjećaju sreću.
Kreativni domaći zadatak. Napravite crtež u pravougaonom koordinatnom sistemu koji se sastoji od segmenata i kreirajte njegov analitički model.
6. Samostalan rad. Diferencirani zadatak (u dvije verzije)
Opcija I:
Skicirajte grafikone funkcija:

Opcija II:
Šematski nacrtajte grafove funkcija za koje su ispunjeni sljedeći uvjeti:

7. Sažetak lekcije
Analiza obavljenog posla. Ocjenjivanje.
Instrukcije
Da biste pronašli koordinate točke na liniji, odaberite je na liniji i nacrtajte okomite linije na koordinatnoj osi. Odredite kojem broju odgovara tačka preseka, presek sa x osom je vrednost apscise, odnosno x1, presek sa y osom je ordinata, y1.
Pokušajte odabrati tačku čije se koordinate mogu odrediti bez frakcijskih vrijednosti, radi praktičnosti i preciznosti proračuna. Za konstruiranje jednačine potrebne su vam najmanje dvije točke. Pronađite koordinate druge tačke koja pripada ovoj pravoj (x2, y2).
Zamijenite vrijednosti koordinata u jednadžbu prave linije koja ima opći oblik y=kx+b. Dobićete sistem od dve jednačine y1=kx1+b i y2=kx2+b. Rešite ovaj sistem, na primer, na sledeći način.
Izraziti b iz prve jednačine i zamijeniti u drugu, pronaći k, zamijeniti u bilo koju jednačinu i naći b. Na primjer, rješenje sistema 1=2k+b i 3=5k+b će izgledati ovako: b=1-2k, 3=5k+(1-2k); 3k=2, k=1,5, b=1-2*1,5=-2. Dakle, jednačina prave linije je y=1,5x-2.
Poznavajući dvije tačke koje pripadaju pravoj, pokušajte koristiti kanonsku jednačinu prave, ona izgleda ovako: (x - x1)/(x2 - x1) = (y - y1)/(y2 - y1). Zamijenite vrijednosti (x1;y1) i (x2;y2), pojednostavite. Na primjer, tačke (2;3) i (-1;5) pripadaju pravoj liniji (x-2)/(-1-2)=(y-3)/(5-3); -3(x-2)=2(y-3); -3x+6=2y-6; 2y=12-3x ili y=6-1.5x.
Da biste pronašli jednadžbu funkcije koja ima nelinearni graf, postupite na sljedeći način. Pogledajte sve standardne grafikone y=x^2, y=x^3, y=√x, y=sinx, y=cosx, y=tgx, itd. Ako vas neko od njih podsjeća na vaš raspored, koristite ga kao osnovu.
Nacrtajte standardni graf osnovne funkcije na istoj koordinatnoj osi i pronađite ga na svom grafikonu. Ako se graf pomjeri nekoliko jedinica gore ili dolje, to znači da je ovaj broj dodan funkciji (na primjer, y=sinx+4). Ako se graf pomjeri udesno ili ulijevo, to znači da je argumentu dodan broj (na primjer, y=sin (x+P/2).
Izduženi graf po visini pokazuje da je funkcija argumenta pomnožena nekim brojem (na primjer, y=2sinx). Ako je graf, naprotiv, smanjen po visini, to znači da je broj ispred funkcije manji od 1.
Usporedite graf osnovne funkcije i vaše funkcije po širini. Ako je uži, tada x prethodi broj veći od 1, širok - broj manji od 1 (na primjer, y=sin0.5x).
Bilješka
Možda graf odgovara pronađenoj jednadžbi samo na određenom segmentu. U ovom slučaju navedite za koje vrijednosti x vrijedi rezultirajuća jednakost.
Prava linija je algebarska linija prvog reda. U kartezijanskom koordinatnom sistemu na ravni, jednačina prave linije je data jednačinom prvog stepena.
Trebaće ti
- Poznavanje analitičke geometrije. Osnovno poznavanje algebre.
Instrukcije
Jednačina je data sa dva preko koje ova prava linija mora proći. Napravimo omjer koordinata ovih tačaka. Neka prva tačka ima koordinate (x1,y1), a druga (x2,y2), tada će jednačina prave linije biti napisana na sljedeći način: (x-x1)/(x2-x1) = (y-y1 )(y2-y1).
Transformirajmo rezultujuću pravolinijsku jednačinu i izrazimo y eksplicitno u terminima x. Nakon ove operacije, jednačina prave linije će poprimiti svoj konačni oblik: y=(x-x1)/((x2-x1)*(y2-y1))+y1.
Video na temu
Bilješka
Ako je jedan od brojeva u nazivniku nula, to znači da je prava paralelna s jednom od koordinatnih osa.
Koristan savjet
Nakon što ste napisali jednačinu linije, provjerite njenu ispravnost. Da biste to učinili, zamijenite koordinate tačaka umjesto odgovarajućih koordinata i uvjerite se da je jednakost zadovoljena.
Često je poznato da y linearno zavisi od x i dat je graf ove zavisnosti. U ovom slučaju moguće je pronaći jednačinu prave. Prvo morate odabrati dvije tačke na pravoj liniji.

Instrukcije
Pronađite odabrane tačke. Da biste to učinili, spustite okomice od tačaka na koordinatnoj osi i zapišite brojeve sa skale. Dakle, za tačku B iz našeg primjera, x koordinata je -2, a y koordinata je 0. Slično, za tačku A koordinate će biti (2;3).
Poznato je da prava ima oblik y = kx + b. Koordinate odabranih tačaka zamjenjujemo u jednačinu u opštem obliku, a zatim za tačku A dobijamo sljedeću jednačinu: 3 = 2k + b. Za tačku B dobijamo još jednu jednačinu: 0 = -2k + b. Očigledno, imamo sistem od dvije jednačine sa dvije nepoznate: k i b.
Zatim rješavamo sistem na bilo koji pogodan način. U našem slučaju moguće je sabirati jednačine sistema, jer je nepoznata k uključena u obje jednačine sa koeficijentima koji su identični po veličini, ali suprotni po predznaku. Tada dobijamo 3 + 0 = 2k - 2k + b + b, ili, što je isto: 3 = 2b. Dakle, b = 3/2. Zamijenite pronađenu vrijednost b u bilo koju od jednadžbi da biste pronašli k. Tada je 0 = -2k + 3/2, k = 3/4.
Zamenimo pronađene k i b u opštu jednačinu i dobijemo željenu jednačinu prave: y = 3x/4 + 3/2.
Video na temu
Bilješka
Koeficijent k se naziva nagibom prave i jednak je tangentu ugla između prave i x-ose.
Iz dvije tačke se može povući prava linija. Koordinate ovih tačaka su „skrivene“ u jednačini prave linije. Jednadžba će vam reći sve tajne o liniji: kako se rotira, na kojoj se strani koordinatne ravnine nalazi itd.

Instrukcije
Češće je potrebno ugraditi u ravninu. Svaka tačka će imati dvije koordinate: x, y. Obratite pažnju na jednačinu, ona ima opšti oblik: y=k*x ±b, gde su k, b slobodni brojevi, a y, x su iste koordinate svih tačaka na pravoj pronađite y koordinatu koju trebate znati x koordinatu Najzanimljivije je to što možete odabrati bilo koju vrijednost za x koordinatu: iz čitave beskonačnosti poznatih brojeva. Zatim, zamijenite x u jednadžbu i riješite je da biste pronašli y. Primjer. Neka je data jednadžba: y=4x-3. Izmislite bilo koje dvije vrijednosti za koordinate dvije tačke. Na primjer, x1 = 1, x2 = 5. Zamijenite ove vrijednosti u jednadžbe da biste pronašli y koordinate. y1 = 4*1 – 3 = 1. y2 = 4*5 – 3 = 17. Dobijamo dvije tačke A i B, A (1; 1) i B (5; 17).
Trebali biste ucrtati pronađene tačke u koordinatnu os, spojiti ih i vidjeti samu pravu liniju koja je opisana jednadžbom. Da biste konstruisali pravu liniju, morate raditi u Dekartovom koordinatnom sistemu. Nacrtajte osi X i Y Postavite vrijednost na "nulu" na mjestu presjeka. Nacrtajte brojeve na osi.
U konstruisanom sistemu označite dve tačke pronađene u koraku 1. Princip postavljanja naznačenih tačaka: tačka A ima koordinate x1 = 1, y1 = 1; na X-osi odaberite broj 1, na Y-osi – broj 1. Tačka A se nalazi u ovoj tački data je vrijednostima x2 = 5, y2 = 17. Po analogiji, pronađite tačku. B na grafikonu. Povežite A i B da napravite pravu liniju.
Video na temu
Termin rješavanje funkcije kao takve se ne koristi u matematici. Ovu formulaciju treba shvatiti kao izvođenje određenih radnji na datu funkciju kako bi se pronašla određena karakteristika, kao i pronalaženje potrebnih podataka za konstruiranje grafa funkcije.

Instrukcije
Možete uzeti u obzir približni dijagram prema kojem je ponašanje funkcije prikladno i izgraditi njen graf.
Pronađite domenu funkcije. Odredite da li je funkcija parna ili neparna. Ako nađete željeni odgovor, nastavite samo na traženoj polu-osi. Odredite da li je funkcija periodična. Ako je odgovor pozitivan, nastavite studiju samo jedan period. Pronađite tačke i odredite njihovo ponašanje u blizini ovih tačaka.
Pronađite točke presjeka grafa funkcije sa koordinatnim osa. Pronađite ih ako postoje. Koristite prvi izvod da ispitate funkciju za ekstreme i intervale monotonosti. Također izvršite studiju koristeći drugi izvod za konveksnost, konkavnost i pregibne tačke. Odaberite točke za preciziranje funkcije i izračunajte vrijednosti funkcije u njima. Konstruirajte graf funkcije, uzimajući u obzir rezultate dobivene iz svih provedenih studija.
Na osi 0X treba identifikovati karakteristične tačke: tačke diskontinuiteta, x = 0, nule funkcije, tačke ekstrema, tačke pregiba. Ove asimptote će dati skicu grafa funkcije.
Dakle, koristeći konkretan primjer funkcije y=((x^2)+1)/(x-1), provedite studiju koristeći prvi izvod. Prepišite funkciju kao y=x+1+2/(x-1). Prvi izvod će biti jednak y’=1-2/((x-1)^2).
Pronađite kritične tačke prve vrste: y’=0, (x-1)^2=2, rezultat će biti dvije tačke: x1=1-sqrt2, x2=1+sqrt2. Dobijene vrijednosti označite na domeni definicije funkcije (slika 1).
Odredite predznak izvoda na svakom od intervala. Na osnovu pravila izmjenjivanja znakova od “+” do “-” i od “-” do “+”, dobijate da je maksimalna tačka funkcije x1=1-sqrt2, a minimalna tačka x2=1+ sqrt2. Isti zaključak se može izvesti iz predznaka drugog izvoda.
klasa: 7
Funkcija zauzima jedno od vodećih mjesta u školskom kursu algebre i ima brojne primjene u drugim naukama. Na početku studije, u svrhu motivacije i aktualizacije problematike, obavještavam vas da se niti jedan fenomen, niti jedan proces u prirodi ne može proučavati, niti jedna mašina ne može konstruisati, a zatim raditi bez potpunog matematičkog opisa. . Jedan alat za ovo je funkcija. Njegovo proučavanje počinje u 7. razredu, djeca se po pravilu ne upuštaju u definiciju. Posebno teško pristupačni koncepti su domen definicije i domen značenja. Koristeći poznate veze između veličina u problemima kretanja i vrijednosti, prevodim ih na jezik funkcije, održavajući vezu s njenom definicijom. Tako učenici razvijaju koncept funkcije na svjesnom nivou. U istoj fazi, mukotrpno se radi na novim konceptima: domen definicije, domen vrijednosti, argument, vrijednost funkcije. Koristim napredno učenje: uvodim oznake D(y), E(y), uvodim pojam nule funkcije (analitički i grafički), pri rješavanju vježbi sa područjima konstantnog predznaka. Što se učenici ranije i češće susreću sa teškim pojmovima, to ih bolje postaju svjesni na nivou dugoročnog pamćenja. Prilikom proučavanja linearne funkcije preporučljivo je pokazati vezu sa rješenjem linearnih jednačina i sistema, a kasnije i sa rješenjem linearnih nejednačina i njihovih sistema. Na predavanju studenti dobijaju veliki blok (modul) novih informacija, pa se na kraju predavanja „iscijedi“ materijal i sastavlja rezime koji studenti moraju znati. Praktične vještine se razvijaju u procesu izvođenja vježbi različitim metodama, koje se zasnivaju na individualnom i samostalnom radu.
1. Neke informacije o linearnim funkcijama.
Linearna funkcija se vrlo često susreće u praksi. Dužina štapa je linearna funkcija temperature. Dužina šina i mostova je takođe linearna funkcija temperature. Udaljenost koju prijeđe pješak, voz ili automobil konstantnom brzinom linearna je funkcija vremena putovanja.
Linearna funkcija opisuje niz fizičkih odnosa i zakona. Pogledajmo neke od njih.
1) l = l o (1+at) – linearno širenje čvrstih tijela.
2) v = v o (1+bt) – volumetrijsko širenje čvrstih tijela.
3) p=p o (1+at) – zavisnost otpornosti čvrstih provodnika od temperature.
4) v = v o + at – brzina jednoliko ubrzanog kretanja.
5) x= x o + vt – koordinata ravnomjernog kretanja.
Zadatak 1. Odredite linearnu funkciju iz tabelarnih podataka:
| X | 1 | 3 |
| at | -1 | 3 |
Rješenje. y= kx+b, problem se svodi na rješavanje sistema jednadžbi: 1=k 1+b i 3=k 3 + b
Odgovor: y = 2x – 3.
Zadatak 2. Krećući se ravnomjerno i pravolinijski, tijelo je prešlo 14 m u prvih 8 s, a 12 m u narednih 4 s. Na osnovu ovih podataka napravite jednačinu kretanja.
Rješenje. Prema uslovima zadatka imamo dve jednačine: 14 = x o +8 v o i 26 = x o +12 v o, rešavajući sistem jednačina, dobijamo v = 3, x o = -10.
Odgovor: x = -10 + 3t.
Zadatak 3. Automobil je napustio grad kretajući se brzinom od 80 km/h. Nakon 1,5 sata za njim je došao motocikl čija je brzina bila 100 km/h. Koliko će dugo trebati motoru da ga sustigne? Na kojoj udaljenosti od grada će se to dogoditi?
Odgovor: 7,5 sati, 600 km.
Zadatak 4. Udaljenost između dvije tačke u početnom trenutku je 300m. Tačke se kreću jedna prema drugoj brzinom od 1,5 m/s i 3,5 m/s. Kada će se sastati? Gdje će se to dogoditi?
Odgovor: 60 s, 90 m.
Zadatak 5. Bakarno ravnalo na 0 o C ima dužinu od 1 m. Naći povećanje njegove dužine kada se njegova temperatura poveća za 35 o, za 1000 o C (tačka topljenja bakra je 1083 o C)
Odgovor: 0,6 mm.
2. Direktna proporcionalnost.
Mnogi zakoni fizike izraženi su direktnom proporcionalnošću. U većini slučajeva, model se koristi za pisanje ovih zakona
u nekim slučajevima -
Navedimo nekoliko primjera.
1. S = v t (v – const)
2. v = a t (a – const, a – ubrzanje).
3. F = kx (Hookeov zakon: F – sila, k – krutost (const), x – elongacija).
4. E= F/q (E je intenzitet u datoj tački električnog polja, E je konstantan, F je sila koja deluje na naelektrisanje, q je veličina naelektrisanja).
Kao matematički model direktne proporcionalnosti možete koristiti sličnost trokuta ili proporcionalnost segmenata (Talesov teorem).
Zadatak 1. Voz je prošao semafor za 5 s, a peron dug 150 m za 15 s. Kolika je dužina voza i njegova brzina?
Rješenje. Neka je x dužina voza, x+150 ukupna dužina voza i perona. U ovom zadatku brzina je konstantna, a vrijeme proporcionalno dužini.
Imamo proporciju: (x+150) :15 = x: 5.
Gdje je x = 75, v = 15.
Odgovori. 75 m, 15 m/s.
Zadatak 2. Čamac je za neko vrijeme prešao 90 km nizvodno. U isto vrijeme, prešao bi 70 km protiv struje. Koliko će daleko putovati splav za ovo vrijeme?
Odgovori. 10 km.
Zadatak 3. Kolika je bila početna temperatura vazduha ako se pri zagrevanju za 3 stepena njegova zapremina poveća za 1% od prvobitne.
Odgovori. 300 K (Kelvin) ili 27 0 C.
Predavanje na temu "Linearna funkcija".
Algebra, 7. razred
1. Razmotrimo primjere problema koristeći dobro poznate formule:
S = v t (formula putanje), (1)
C = ck (formula vrijednosti). (2)
Zadatak 1. Automobil se odvezao 20 km od tačke A i nastavio put brzinom od 62 km/h. Na kojoj udaljenosti od tačke A će automobil biti nakon t sati? Sastavite izraz za zadatak, označavajući udaljenost S, pronađite ga na t = 1 sat, 2,5 sata, 4 sata.
1) Pomoću formule (1) nalazimo put koji pređe automobil brzinom od 62 km/h u vremenu t, S 1 = 62t;
2) Tada će od tačke A nakon t sati automobil biti na udaljenosti S = S 1 + 20 ili S = 62t + 20, pronađimo vrijednost S:
pri t = 1, S = 62*1 + 20, S = 82;
pri t = 2,5, S = 62*2,5 + 20, S = 175;
pri t = 4, S = 62*4+ 20, S = 268.
Napominjemo da se pri pronalaženju S mijenja samo vrijednost t i S, tj. t i S su varijable, a S zavisi od t, svaka vrijednost t odgovara jednoj vrijednosti S. Označavajući varijablu S sa Y, a t sa x, dobijamo formulu za rješavanje ovog problema:
Y= 62x + 20. (3)
Problem 2. U prodavnici smo kupili udžbenik za 150 rubalja i 15 sveska po n rubalja. Koliko ste novca platili za kupovinu? Sastavite izraz za zadatak, koji označava trošak C, pronađite ga za n = 5,8,16.
1) Koristeći formulu (2) nalazimo cenu sveske C 1 = 15n;
2) Tada je trošak cijele kupovine C = C 1 +150 ili C = 15n+150, pronađimo vrijednost C:
sa n = 5, C = 15 5 + 150, C = 225;
sa n = 8, C = 15 8 + 150, C = 270;
sa n = 16, C = 15 16+ 150, C = 390.
Slično tome, primjećujemo da su C i n varijable, za svaku vrijednost n odgovara jedna vrijednost C. Označavajući varijablu C kao Y, a n kao x, dobijamo formulu za rješavanje problema 2:
Y= 15x + 150. (4)
Upoređujući formule (3) i (4), uvjerili smo se da se varijabla Y nalazi kroz varijablu x korištenjem istog algoritma. Razmotrili smo samo dva različita problema koji opisuju fenomene koji nas svakodnevno okružuju. Naime, postoji mnogo procesa koji se mijenjaju prema dobijenim zakonima, pa takva zavisnost između varijabli zaslužuje proučavanje.
Rješenja problema pokazuju da se vrijednosti varijable x biraju proizvoljno, zadovoljavajući uslove problema (pozitivne u zadatku 1 i prirodne u zadatku 2), tj. x je nezavisna varijabla (naziva se argument), i Y je zavisna varijabla i između njih postoji korespondencija jedan-na-jedan, a po definiciji je takva ovisnost funkcija. Stoga, označavajući koeficijent x slovom k, a slobodni pojam slovom b, dobijamo formulu
Y= kx + b.
Definicija: Funkcija forme y= kx + b, gdje su k, b neki brojevi, x je argument, y je vrijednost funkcije koja se naziva linearna funkcija.
Da bismo proučavali svojstva linearne funkcije, uvodimo definicije.
Definicija 1. Skup dopuštenih vrijednosti nezavisne varijable naziva se domenom definicije funkcije (dopustivo - to znači one numeričke vrijednosti x za koje se vrše proračuni y) i označava se D(y).
Definicija 2. Skup vrijednosti zavisne varijable naziva se domena funkcije (to su numeričke vrijednosti koje y uzima) i označava se E(y).
Definicija 3. Graf funkcije je skup tačaka na koordinatnoj ravni čije koordinate pretvaraju formulu u pravu jednakost.
Definicija 4. Koeficijent k od x naziva se nagib.
Razmotrimo svojstva linearne funkcije.
1. D(y) – svi brojevi (množenje je definisano na skupu svih brojeva).
2. E(y) – svi brojevi.
3. Ako je y = 0, tada je x = -b/k, tačka (-b/k;0) – tačka preseka sa Ox osom, naziva se nula funkcije.
4. Ako je x = 0, onda je y = b, tačka (0; b) je tačka preseka sa Oy osom.
5. Pronađimo na kojoj će liniji linearna funkcija na koordinatnoj ravni poravnati tačke, tj. koji je graf funkcije. Da biste to učinili, razmotrite funkcije
1) y= 2x + 3, 2) y= -3x – 2.
Za svaku funkciju napravićemo tablicu vrijednosti. Postavimo proizvoljne vrijednosti varijable x i izračunajmo odgovarajuće vrijednosti varijable Y.
| X | -1,5 | -2 | 0 | 1 | 2 |
| Y | 0 | -1 | 3 | 5 | 7 |

Nakon što smo konstruirali rezultirajuće parove (x; y) na koordinatnoj ravni i povezali ih za svaku funkciju posebno (uzeli smo x vrijednosti s korakom od 1, ako smanjimo korak, točke će se češće redati, a ako je korak blizu nule, tada će se tačke spojiti u punu liniju ), primjećujemo da su tačke postavljene u pravu liniju u slučaju 1) i u slučaju 2). Zbog činjenice da se funkcije biraju proizvoljno (sagradite svoje grafike y= 0,5x – 4, y= x + 5), zaključujemo da da je graf linearne funkcije prava linija. Koristeći svojstvo prave: kroz dvije tačke prolazi samo jedna ravna linija, dovoljno je uzeti dvije tačke za konstruiranje prave linije.
6. Iz geometrije je poznato da se prave mogu ili seći ili biti paralelne. Proučimo relativni položaj grafova nekoliko funkcija.
1) y= -x + 5, y= -x + 3, y= -x – 4; 2) y= 2x + 2, y= x + 2, y= -0,5x + 2.
Napravimo grupe grafikona 1) i 2) i izvučemo zaključke.
|
 |
Grafovi funkcija 1) nalaze se paralelno, ispitujući formule, primjećujemo da sve funkcije imaju iste koeficijente za x.
Grafovi funkcija 2) seku u jednoj tački (0;2). Ispitujući formule, primjećujemo da su koeficijenti različiti, a broj b = 2.
Osim toga, lako je primijetiti da prave linije definirane linearnim funkcijama sa k › 0 formiraju oštar ugao s pozitivnim smjerom ose Ox, a tupi ugao sa k ‹ 0. Stoga se koeficijent k naziva koeficijent nagiba.
7. Razmotrimo posebne slučajeve linearne funkcije u zavisnosti od koeficijenata.
1) Ako je b=0, tada funkcija poprima oblik y= kx, zatim k = y/x (omjer pokazuje koliko je puta razlika ili koliki je dio y od x).
Funkcija oblika Y= kx naziva se direktna proporcionalnost. Ova funkcija ima sva svojstva linearne funkcije, njena posebnost je da je za x=0 y=0. Graf direktne proporcionalnosti prolazi kroz početnu tačku (0;0).
2) Ako je k = 0, tada funkcija poprima oblik y = b, što znači da za bilo koju vrijednost x funkcija poprima istu vrijednost.
Funkcija oblika y = b naziva se konstantna. Grafikon funkcije je prava linija koja prolazi kroz tačku (0;b) paralelnu sa Ox osom u b=0, grafik konstantne funkcije poklapa se sa osom apscisa.
Abstract
1. Definicija Funkcija oblika Y = kx + b, gdje su k, b neki brojevi, x je argument, Y je vrijednost funkcije, naziva se linearna funkcija.
D(y) – svi brojevi.
E(y) – svi brojevi.
Grafikon linearne funkcije je prava linija koja prolazi kroz tačku (0;b).
2. Ako je b=0, tada funkcija poprima oblik y= kx, koji se naziva direktna proporcionalnost. Graf direktne proporcionalnosti prolazi kroz ishodište.
3. Ako je k = 0, tada funkcija poprima oblik y= b i naziva se konstantnom. Graf konstantne funkcije prolazi kroz tačku (0;b), paralelno sa apscisnom osom.
4. Međusobni raspored grafova linearnih funkcija.
Date su funkcije y= k 1 x + b 1 i y= k 2 x + b 2.
Ako je k 1 = k 2, onda su grafovi paralelni;
Ako k 1 i k 2 nisu jednaki, grafovi se sijeku.
5. Vidi gore za primjere grafova linearnih funkcija.
Književnost.
- Udžbenik Yu.N. Makarychev, N.G. Mindyuk, K.I. Neshkov i drugi. “Algebra, 8.”
- Didaktički materijali iz algebre za 8. razred / V.I. Zhokhov, Yu.N. Makarychev, N.G. Mindyuk. – M.: Obrazovanje, 2006. – 144 str.
- Dodatak listu 1. septembar „Matematika“, 2001, br. 2, br.
Maslova Angelina
Istraživački rad iz matematike. Angelina je sastavila kompjuterski model linearne funkcije koji je koristila za istraživanje.
Skinuti:
Pregled:
Opštinska autonomna obrazovna ustanova srednja škola br. 8 gradskog okruga Bor, oblast Nižnji Novgorod
Istraživački rad u informatici i matematici
Završila učenica 7A odeljenja Angelina Maslova
Rukovodilac: nastavnik informatike, Voronina Anna Alekseevna.
Urbani okrug Bor - 2015
Uvod
- Istraživanje linearnih funkcija u proračunskim tablicama
Zaključak
Bibliografija
Uvod
Ove godine na časovima algebre upoznali smo se sa linearnim funkcijama. Naučili smo da gradimo graf linearne funkcije, odredili kako treba da se ponaša graf funkcije u zavisnosti od njenih koeficijenata. Nešto kasnije, na lekciji informatike, naučili smo da se ove radnje mogu smatrati matematičkim modeliranjem. Odlučio sam vidjeti da li je moguće istražiti linearnu funkciju pomoću proračunskih tablica.
Cilj rada: istražiti linearnu funkciju u proračunskim tablicama
Ciljevi istraživanja:
- pronaći i proučavati informacije o linearnoj funkciji;
- izgraditi matematički model linearne funkcije u tabeli;
- istražiti linearnu funkciju koristeći konstruirani model.
Predmet studija:matematičko modeliranje.
Predmet studija:matematički model linearne funkcije.
Modeliranje kao metoda spoznaje
Čovek doživljava svet skoro od svog rođenja. Da bi to učinila, osoba koristi modele koji mogu biti vrlo raznoliki.
Model je novi objekat koji odražava neka bitna svojstva stvarnog objekta.
Modeli stvarnih objekata koriste se u raznim situacijama:
- Kada je objekt vrlo velik (na primjer, Zemlja je model: globus ili mapa) ili, obrnuto, premali (biološka ćelija).
- Kada je objekat veoma složen po svojoj strukturi (automobil - model: dečiji auto).
- Kada je objekt opasan za proučavanje (vulkan).
- Kada je objekat veoma udaljen.
Modeliranje je proces stvaranja i proučavanja modela.
Sami kreiramo i koristimo modele, ponekad i ne razmišljajući o tome. Na primjer, fotografiramo neki događaj u svom životu, a zatim ih pokažemo prijateljima.
Na osnovu vrste informacija, svi modeli se mogu podijeliti u nekoliko grupa:
- Verbalni modeli. Ovi modeli mogu postojati u usmenom ili pismenom obliku. To može biti samo verbalni opis predmeta ili pjesme, ili može biti novinski članak ili esej - sve su to verbalni modeli.
- Grafički modeli. Ovo su naši crteži, fotografije, dijagrami i grafikoni.
- Ikonični modeli. To su modeli napisani nekim simboličkim jezikom: bilješke, matematičke, fizičke ili kemijske formule.
Linearna funkcija i njena svojstva
Linearna funkcijanaziva se funkcija forme
Grafikon linearne funkcije je prava linija.
1 . Za crtanje funkcije, potrebne su nam koordinate dvije tačke koje pripadaju grafu funkcije. Da biste ih pronašli, trebate uzeti dvije vrijednosti x, zamijeniti ih u jednadžbu funkcije i koristiti ih za izračunavanje odgovarajućih y vrijednosti.
Na primjer, za crtanje funkcije, pogodan za uzimanje i , tada će ordinate ovih tačaka biti jednake i .
Dobijamo tačke A(0;2) i B(3;3). Povežimo ih i dobijemo graf funkcije:

2 . U jednadžbi funkcije y=kx+b, koeficijent k je odgovoran za nagib grafa funkcije:
Koeficijent b je odgovoran za pomicanje grafika duž ose OY:
Na slici ispod prikazani su grafikoni funkcija; ;

Imajte na umu da je u svim ovim funkcijama koeficijent veći od nule desno . Štaviše, veća je vrijednost, što je prava linija strmija.
U svim funkcijama– i vidimo da svi grafovi sijeku osu OY u tački (0;3)
Pogledajmo sada grafove funkcija; ;

Ovaj put u svim funkcijama koeficijent manje od nule , a svi grafovi funkcija su nagnuti lijevo . Koeficijent b je isti, b=3, a grafovi, kao iu prethodnom slučaju, sijeku osu OY u tački (0;3)
Pogledajmo grafove funkcija; ;

Sada u svim jednadžbama funkcije koeficijentisu jednaki. I dobili smo tri paralelne prave.
Ali koeficijenti b su različiti, a ovi grafovi sijeku os OY u različitim tačkama:
Grafikon funkcije (b=3) siječe osu OY u tački (0;3)
Grafikon funkcije (b=0) seče osu OY u tački (0;0) - ishodištu.
Grafikon funkcije (b=-2) siječe osu OY u tački (0;-2)
Dakle, ako znamo predznake koeficijenata k i b, onda možemo odmah zamisliti kako izgleda graf funkcije.
Ako je k 0, zatim graf funkcije ima oblik:

Ako je k>0 i b>0, zatim graf funkcije ima oblik:

Ako je k>0 i b , zatim graf funkcije ima oblik:

ako k, zatim graf funkcije ima oblik:

Ako je k=0, tada je funkcija pretvara u funkcijua njegov graf izgleda ovako:

Ordinate svih tačaka na grafu funkcije jednaka
Ako je b=0 , zatim graf funkcijeprolazi kroz ishodište:

4. Uslov za paralelnost dve prave:
Grafikon funkcije paralelno sa grafikom funkcije, Ako
5. Uslov za okomitost dvije prave:
Grafikon funkcije okomito na graf funkcije, ako ili
6 . Točke presjeka funkcijskog grafasa koordinatnim osama.
Sa OY osovinom. Apscisa bilo koje tačke koja pripada osi OY jednaka je nuli. Stoga, da biste pronašli točku presjeka sa OY osom, trebate zamijeniti nulu u jednadžbi funkcije umjesto x. Dobijamo y=b. To jest, tačka preseka sa OY osom ima koordinate (0; b).
Sa OX osom: Ordinata bilo koje tačke koja pripada osi OX jednaka je nuli. Stoga, da biste pronašli točku presjeka sa OX osom, trebate zamijeniti nulu u jednadžbi funkcije umjesto y. Dobijamo 0=kx+b. Odavde. To jest, tačka preseka sa OX osom ima koordinate (;0):

Istraživanje linearnih funkcija u proračunskim tablicama
Da bih proučavao linearnu funkciju u okruženju proračunskih tablica, sastavio sam sljedeći algoritam:
- Konstruirajte matematički model linearne funkcije u proračunskoj tablici.
- Popunite tablicu praćenja vrijednosti argumenata i funkcija.
- Iscrtajte linearnu funkciju pomoću Čarobnjaka za grafikone.
- Istražite linearnu funkciju ovisno o vrijednostima koeficijenata.
Za proučavanje linearne funkcije koristio sam Microsoft Office Excel 2007. Koristio sam formule za kompajliranje tablica vrijednosti argumenata i funkcija. Dobio sam sledeću tabelu vrednosti:
Koristeći takav matematički model, možete lako pratiti promjene na grafu linearne funkcije mijenjajući vrijednosti koeficijenata u tablici.
Također, koristeći proračunske tablice, odlučio sam pratiti kako se mijenja relativna pozicija grafova dvije linearne funkcije. Nakon što sam napravio novi matematički model u tabeli, dobio sam sljedeći rezultat:
Promjenom koeficijenata dviju linearnih funkcija jasno sam se uvjerio u valjanost informacija koje sam saznao o svojstvima linearnih funkcija.
Zaključak
Linearna funkcija u algebri smatra se najjednostavnijom. Ali u isto vrijeme ima mnoga svojstva koja nisu odmah jasna. Nakon što sam izgradio matematički model linearne funkcije u proračunskim tablicama i ispitao ga, svojstva linearne funkcije su mi postala jasnija. Jasno sam mogao vidjeti kako se graf mijenja kada se mijenjaju koeficijenti funkcije.
Mislim da će matematički model koji sam napravio pomoći učenicima sedmog razreda da samostalno istraže linearnu funkciju i bolje je razumiju.
Bibliografija
- Udžbenik algebre za 7. razred.
- Udžbenik informatike za 7. razred
- Wikipedia.org
Pregled:
Da biste koristili preglede prezentacija, kreirajte Google račun i prijavite se na njega: https://accounts.google.com
Naslovi slajdova:
Predmet proučavanja: linearna funkcija. Predmet istraživanja: matematički model linearne funkcije.
Svrha rada: istražiti linearnu funkciju u tabelama Ciljevi istraživanja: pronaći i proučiti informacije o linearnoj funkciji; izgraditi matematički model linearne funkcije u tabeli; istražiti linearnu funkciju koristeći konstruirani model.
Linearna funkcija je funkcija oblika y= k x+ b, gdje je x argument, a k i b su neki brojevi (koeficijenti).
Razmotrimo funkciju y=kx+b takvu da je k 0 , b=0 . Pogled: y=kx U jednom koordinatnom sistemu ćemo konstruisati grafove ovih funkcija: y=3x y=x y=-7x Svaki graf ćemo konstruisati sa odgovarajućom bojom x 0 1 y 0 3 x 0 1 y 0 1 x 0 1 y 0 7
Graf linearne funkcije oblika y = k x prolazi kroz ishodište. y=x y=3x y=-7x y x
Zaključak: Grafikon linearne funkcije oblika y = kx + b siječe O Y osu u tački (0; b).
Razmotrimo funkciju y=kx+b, gdje je k=0. Pogled: y=b U jednom koordinatnom sistemu konstruišite grafove funkcija: y=4 y=-3 y=0 Svaki graf konstruišemo odgovarajućom bojom
Grafikon linearne funkcije oblika y = b ide paralelno sa OX osom i siječe O Y osu u tački (0; b). y=4 y=-3 y=0 y x
U jednom koordinatnom sistemu konstruišite grafove funkcija: Y=2x Y=2x+ 3 Y=2x-4 Svaki graf konstruišemo odgovarajuće boje x 0 1 y 0 2 x 0 1 y 3 5 x 0 1 y -4 -2
Grafovi linearnih funkcija oblika y=kx+b su paralelni ako su koeficijenti za x isti. y =2x+ 3 y =2x y =2x-4 y x
U jednom koordinatnom sistemu ćemo konstruisati grafove funkcija: y=3x+4 Y= - 2x+4 Konstruisaćemo grafove odgovarajuće boje x 0 1 y 4 7 x 0 1 y 4 2
Grafovi dvije linearne funkcije oblika y=kx+b se sijeku ako su koeficijenti od x različiti. y x
U jednom koordinatnom sistemu ćemo konstruisati grafove funkcija: y=0, 5x-2 y=-2x-4 y= 4 x-1 y=- 0, 2 5 x- 3 x 0 4 y x 0 -2 y -4 0 x 0 4 y -2 0 x 0 1 y -1 3 x 0 - 4 y -3 -2
y=0, 5x-2 y=-2x-4 y= 4 x-1 y=- 0, 2 5 x- 3 Grafovi dviju linearnih funkcija oblika y=kx+b međusobno su okomiti ako je proizvod koeficijenti od x je “-1” .
Stoga se koeficijent k naziva nagibom prave linije - grafikom funkcije y=kx+ b. Ako je k 0, tada je ugao nagiba grafika prema O X osi oštar. Funkcija se povećava. y x y x
Tabela
Tabela
Linearne jednadžbe Algebarski uslov Geometrijski izvod y = k 1 x+ b 1 k 1 = k 2, b 1 ≠ b 2 y = k 2 x+ b 2 k 1 = k 2, b 1 = b 2 k 1 ≠ k 2 k 1 * do 2 = -1 Prave su paralelne Prave se poklapaju Prave su okomite Prave se seku
Matematički model koji sam napravio pomoći će učenicima sedmog razreda da samostalno istraže linearnu funkciju i bolje je razumiju.

