उतार-चढ़ाव वसंत पेंडुलम की पूर्ण यांत्रिक ऊर्जा का सूत्र। मुक्त oscillations। वसंत पेंडुलम। वसंत पेंडुलम परिभाषाएं

परिभाषा 1।

नि: शुल्क आवेश पूरे सिस्टम की संतुलन स्थिति से हटाने के बाद ही आंतरिक बलों की कार्रवाई के तहत किया जा सकता है।

ताकि दोलिक हार्मोनिक कानून के अनुसार बनाया गया हो, यह आवश्यक है कि शरीर को संतुलन स्थिति में लौटने वाली बल संतुलन की स्थिति से पूर्वाग्रह के लिए आनुपातिक थी और विस्थापन के विपरीत पक्ष को निर्देशित किया गया है।

F (t) \u003d m a (t) \u003d - m ω 2 x (t)।

अनुपात से पता चलता है कि ω हार्मोनिक ऑसीलेशन की आवृत्ति है। यह संपत्ति डंगल कानून की प्रयोज्यता के भीतर लोचदार बल की विशेषता है:

एफ यू पी पी \u003d - के एक्स।

परिभाषा 2।

किसी भी प्रकृति की ताकतें जो स्थिति को संतुष्ट करती हैं अर्ध लोचदार.

यही है, एक बड़े पैमाने पर भार, जो चित्रा 2 में दिखाए गए एक निश्चित अंत के साथ कठोरता के वसंत से जुड़ा हुआ है। 2। 1, घर्षण बल की अनुपस्थिति में हार्मोनिक मुक्त oscillations प्रदर्शन करने में सक्षम एक प्रणाली बनाओ।

परिभाषा 3।

वसंत पर स्थित कार्गो को एक रैखिक हार्मोनिक ऑसीलेटर कहा जाता है।

चित्र 2 . 2 . 1 . वसंत पर कार्गो oscillations। कोई घर्षण नहीं है।

परिपत्र आवृत्ति

परिपत्र आवृत्ति ω 0 की नींव न्यूटन के दूसरे कानून के सूत्र को लागू करके बनाई गई है:

एम ए \u003d - के x \u003d m ω 0 2 x।

तो हमें मिलता है:

परिभाषा 4।

आवृत्ति ω 0 कहा जाता है ऑसीलेटर सिस्टम की अपनी आवृत्ति.

वसंत टी पर कार्गो के हार्मोनिक कंपन की अवधि का निर्धारण सूत्र से है:

टी \u003d 2 π ω 0 \u003d 2 π एम के।

वसंत-कार्गो प्रणाली का क्षैतिज स्थान, गुरुत्वाकर्षण को समर्थन प्रतिक्रिया की शक्ति से मुआवजा दिया जाता है। वसंत पर कार्गो लटकते समय, गुरुत्वाकर्षण की दिशा कार्गो की प्रवाह रेखा के साथ जाती है। खिंचाव वसंत की संतुलन स्थिति है:

एक्स 0 \u003d एम जी के, जबकि दोलन नए संतुलन राज्य के पास किया जाता है। उपरोक्त अभिव्यक्तियों में अपनी आवृत्ति ω 0 और दोलन अवधि टी का सूत्र उचित हैं।

परिभाषा 5।

शरीर के त्वरण और समन्वय के बीच मौजूदा गणितीय कनेक्शन के साथ, ऑसीलेटरी सिस्टम का व्यवहार सख्त विवरण द्वारा विशेषता है: त्वरण समय टी द्वारा शरीर x के समन्वय का दूसरा व्युत्पन्न है:

वसंत पर एक माल के साथ न्यूटन के दूसरे कानून का विवरण रिकॉर्ड किया जाएगा:

एम ए - एम एक्स \u003d - के एक्स, या एक्स ¨ + ω 0 2 x \u003d 0, जहां फ्री फ्रीक्वेंसी ω 0 2 \u003d के एम।

यदि भौतिक प्रणाली फॉर्मूला एक्स ¨ + ω 0 2 x \u003d 0 पर निर्भर करती है, तो वे विभिन्न आयामों के साथ मुफ्त ऑसीलेटरी हार्मोनिक आंदोलनों को करने में सक्षम हैं। यह संभव है क्योंकि एक्स \u003d एक्स एम कॉस का उपयोग किया जाता है (ω टी + φ 0)।

फॉर्म एक्स ¨ + ω 0 2 x \u003d 0 का समीकरण नाम मिला मुक्त oscillations के समीकरण। उन्हें भौतिक गुण केवल अपनी ऑसीलेशन आवृत्तियों ω 0 या टी की अवधि।

आयाम एक्स एम और प्रारंभिक चरण φ 0 उस विधि का उपयोग करके पाया जाता है जो उन्हें प्रारंभिक समय की संतुलन स्थिति से प्राप्त करता है।

उदाहरण 1।

संतुलन स्थिति से एक विस्थापित कार्गो की उपस्थिति में, दूरी δ एल और टी \u003d 0 के बराबर समय का क्षण, यह प्रारंभिक गति के बिना कम हो जाता है। फिर x m \u003d δ l, φ 0 \u003d 0। यदि भार संतुलन स्थिति में था, तो प्रारंभिक वेग ± υ 0 प्रेषित किया जाता है जब प्रारंभिक वेग प्रसारित किया जाता है, यहां से x m \u003d m k υ 0, φ 0 \u003d ± π 2।

प्रारंभिक चरण φ 0 के साथ आयाम एक्स एम प्रारंभिक स्थितियों की उपस्थिति से निर्धारित किया जाता है।

चित्र 2। 2। 2। वसंत पर मुफ्त कार्गो oscillations का मॉडल।

मैकेनिकल ऑसीलेटर सिस्टम उनमें से प्रत्येक में लोचदार विकृतियों की धाराओं की उपस्थिति से प्रतिष्ठित हैं। चित्र 2। 2। 2 हार्मोनिक ऑसीलेटर के कोने एनालॉग दिखाता है, जो कंपन बनाता है। डिस्क क्षैतिज रूप से द्रव्यमान के केंद्र में एक लोचदार धागे पर लटक रही है। यदि इसे कोण पर घुमाया जाता है, तो घुमावदार एम वाई पी पी पी के लोचदार विरूपण के बल का क्षण:

एम वाई पी पी \u003d - एक्स θ।

यह अभिव्यक्ति मोड़ के विरूपण के लिए गले के कानून के अनुरूप नहीं है। एक्स का मान वसंत की कचरा के समान है। डिस्क की घूर्णन गति के लिए न्यूटन के दूसरे कानून का रिकॉर्ड लेता है

मैं ε \u003d m y p p \u003d - x θ या θ ¨ \u003d - x θ, जहां जड़ता का क्षण I \u003d I C द्वारा दर्शाया गया है, और ε एक कोणीय त्वरण है।

इसी तरह वसंत पेंडुलम सूत्र के लिए:

ω 0 \u003d x i, t \u003d 2 π i x।

एक मोड़ पेंडुलम का उपयोग यांत्रिक घड़ी में देखा जाता है। उन्हें बैलेंसर का नाम मिला, जिसमें एक सर्पिल के आकार के वसंत का उपयोग करके लोचदार बलों के क्षण का निर्माण किया जाता है।

चित्र 2। 2। 3। कूल पेंडुलम।

यदि आपको पाठ में कोई गलती दिखाई देती है, तो कृपया इसे चुनें और Ctrl + Enter दबाएं

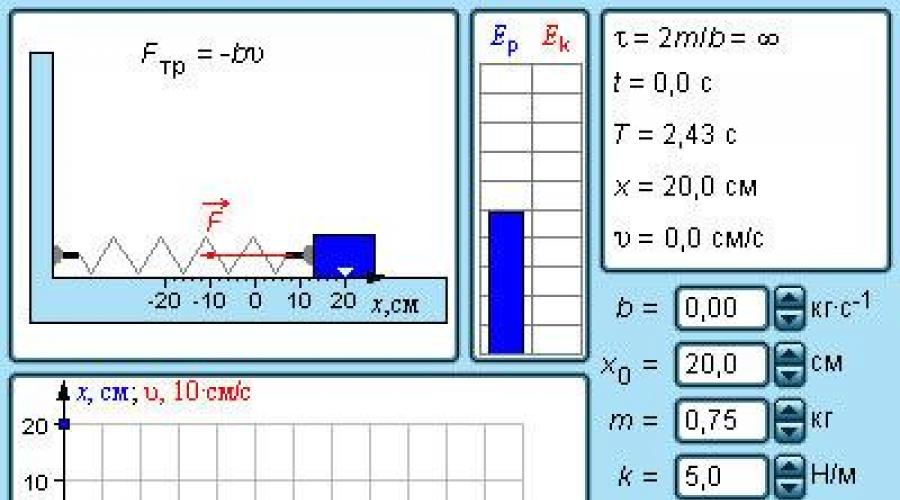
वसंत पेंडुलम एक ऑसीलेटरी प्रणाली है जिसमें टी और वसंत का वजन एक भौतिक बिंदु होता है। एक क्षैतिज वसंत पेंडुलम (चित्र 1, ए) पर विचार करें। यह एक विशाल शरीर मध्य में ड्रिल किया गया है और क्षैतिज रॉड पर रखा गया है, जिसके साथ यह घर्षण (आदर्श oscillatory प्रणाली) के बिना स्लाइड कर सकते हैं। रॉड को दो लंबवत समर्थन के बीच तय किया गया है।

एक दुल्हन प्रतिरोधी वसंत शरीर से एक छोर से जुड़ा हुआ है। इसके अंत का दूसरा अंत समर्थन पर तय किया गया है, जो सबसे सरल मामले में जड़त्वीय संदर्भ प्रणाली के बारे में शांति में है, जिसमें पेंडुलम के ऑसीलेशन होते हैं। वसंत की शुरुआत में विकृत नहीं हुआ है, और शरीर सी की संतुलन स्थिति में है। यदि वसंत को खींचना या निचोड़ा हुआ है, तो शरीर को संतुलन की स्थिति से हटा दें, फिर लोच की शक्ति की तरफ शुरू हो जाएगी विकृत वसंत, संतुलन की शक्ति शुरू हो जाएगी।

हम वसंत को निचोड़ने दें, शरीर को स्थिति में ले जाएं, और जाने दें। लोच की ताकत की कार्रवाई के तहत, यह त्वरित हो जाएगा। साथ ही, लोच की अधिकतम शक्ति शरीर पर मान्य है, क्योंकि एक्स एम स्प्रिंग्स की पूर्ण वृद्धि सबसे बड़ी है। नतीजतन, इस स्थिति में, अधिकतम त्वरण। जब शरीर संतुलन की स्थिति में जाता है, तो वसंत की पूर्ण विस्तार कम हो जाती है, और इसलिए, बल द्वारा लोच द्वारा रिपोर्ट की गई त्वरण कम हो जाती है। लेकिन चूंकि इस आंदोलन में त्वरण गति से लेपित होता है, इसलिए पेंडुलम की गति बढ़ जाती है और संतुलन स्थिति में यह अधिकतम होगा।

संतुलन सी की स्थिति तक पहुंचने के बाद, शरीर बंद नहीं होगा (हालांकि वसंत इस स्थिति में विकृत नहीं है, और लोच की ताकत शून्य है), और गति होने के बाद, वसंत को खींचने, जड़ता पर चले जाएंगे। लोच की उभरती बल अब शरीर के आंदोलन के खिलाफ निर्देशित है और धीमा हो जाता है। बिंदु डी पर, शरीर की गति शून्य होगी, और त्वरण अधिकतम रूप से है, शरीर एक पल के लिए रुक जाएगा, जिसके बाद लोच विपरीत दिशा में, संतुलन की स्थिति में आगे बढ़ना शुरू हो जाएगा। उसे जड़ता, शरीर, वसंत को निचोड़ने और आंदोलन को धीमा करने से, बिंदु ए तक पहुंचता है (चूंकि कोई घर्षण नहीं है), यानी पूर्ण पूर्ण दोलन। उसके बाद, शरीर के आंदोलन को वर्णित अनुक्रम में दोहराया जाएगा। इसलिए, वसंत पेंडुलम के मुक्त oscillations के कारण वसंत के विरूपण के दौरान उत्पन्न लोच की शक्ति का प्रभाव, और शरीर की उत्पीड़न के दौरान उत्पन्न होती है।

गले के कानून के अनुसार एफ एक्स \u003d-केएक्स। न्यूटन एफ एक्स \u003d एमए एक्स के दूसरे कानून के अनुसार। नतीजतन, मा एक्स \u003d-केएक्स। यहां से

वसंत पेंडुलम आंदोलन के गतिशील समीकरण।

हम देखते हैं कि त्वरण सीधे आगे बढ़ रहा है और विपरीत निर्देशित है। हार्मोनिक ऑसीलेशन समीकरण के साथ प्राप्त समीकरण की तुलना हम देखते हैं कि वसंत पेंडुलम एक चक्रीय आवृत्ति के साथ हार्मोनिक ऑसीलेशन करता है

वसंत पेंडुलम के oscillations की अवधि।

एक ही सूत्र में, ऊर्ध्वाधर वसंत पेंडुलम के oscillations की अवधि की गणना की जा सकती है (चित्र 1. बी)। दरअसल, संतुलन की स्थिति में, गुरुत्वाकर्षण की क्रिया के कारण, वसंत पहले से ही x 0 के एक निश्चित मान पर फैला हुआ है, जो अनुपात एमजी \u003d केएक्स 0 द्वारा निर्धारित किया जाता है। जब पेंडुलम लोच के बल के एक्स प्रक्षेपण पर समतोल स्थिति ओ को प्रदर्शित करता है

यदि आप दूरी एक्स पर संतुलन स्थिति से गेंद को स्थानांतरित करते हैं, तो वसंत का विस्तार δl 0 + x के बराबर हो जाएगा। फिर परिणामी बल एक मूल्य लेगा:

संतुलन की स्थिति को ध्यान में रखते हुए (1.7.1), हमें मिलता है:

"माइनस" संकेत से पता चलता है कि विस्थापन और शक्ति के विपरीत दिशाएं हैं।

लोचदार ताकत एफ में निम्नलिखित गुण हैं:

1. यह संतुलन स्थिति से गेंद के विस्थापन के आनुपातिक है;
2. यह हमेशा संतुलन की स्थिति की ओर निर्देशित होता है।

विस्थापन प्रणाली x को सूचित करने के लिए, आपको लोचदार ताकत के खिलाफ नौकरी करने की आवश्यकता है:

यह काम संभावित ऊर्जा प्रणाली का भंडार बनाने के लिए जाता है:

लोचदार ताकत की कार्रवाई के तहत, गेंद लगातार बढ़ती गति के साथ संतुलन की स्थिति में चली जाएगी। इसलिए, प्रणाली की संभावित ऊर्जा कम हो जाएगी, लेकिन गतिशील ऊर्जा बढ़ जाती है (स्प्रिंग्स की उपेक्षा का वजन)। समतुल्य स्थिति में आते हैं, गेंद जड़ता से आगे बढ़ना जारी रखेगी। यह एक धीमी गति है और रुक जाता है जब गतिशील ऊर्जा पूरी तरह से संभावित रूप से गुजरती है। फिर एक ही प्रक्रिया तब बहती होगी जब गेंद विपरीत दिशा में चलती है। यदि सिस्टम में कोई घर्षण नहीं है, तो गेंद लंबे समय तक उतार-चढ़ाव करेगी।

इस मामले में न्यूटन के दूसरे कानून के समीकरण में फॉर्म है:

हम इस तरह के समीकरण को बदल देते हैं:

पदनाम में प्रवेश, हम एक रैखिक सजातीय द्वितीय क्रम विभेदक समीकरण प्राप्त करते हैं:

प्रत्यक्ष प्रतिस्थापन यह सुनिश्चित करना आसान है कि समीकरण (1.7.8) का सामान्य समाधान फॉर्म है:

जहां एक आयाम और φ - oscillations का प्रारंभिक चरण - स्थायी मूल्य। नतीजतन, वसंत पेंडुलम की उतार-चढ़ाव सामंजस्यपूर्ण है (चित्र 1.7.2)।

अंजीर। 1.7.2। हार्मोनिक ऑसीलेशन

कोसाइन की आवधिकता के कारण, ऑसीलेटर सिस्टम के विभिन्न राज्यों को एक निश्चित अवधि (ऑसीलेशन की अवधि) टी के बाद दोहराया जाता है, जिसके लिए ऑसीलेशन चरण बढ़ता है 2π। समानता का उपयोग करके अवधि की गणना करें:

निम्न से कहां से:

समय की प्रति इकाई oscillations की संख्या आवृत्ति कहा जाता है:

इस तरह की आवृत्ति की आवृत्ति आवृत्ति की प्रति इकाई ली जाती है, जिसकी अवधि 1 एस है। इस तरह की एक इकाई को 1 हर्ट्ज कहा जाता है।

(1.7.11) से यह इस प्रकार है कि:

नतीजतन, ω 0 2π सेकंड में किए गए ऑसीलेशन की संख्या है। Ω 0 का मान एक परिपत्र या चक्रीय आवृत्ति कहा जाता है। (1.7.12) और (1.7.13) का उपयोग करके, लिखें:

अलग-अलग () समय पर, हमें एक गेंद की गति अभिव्यक्ति मिलती है:

(1.7.15) से यह इस प्रकार है कि गति हार्मोनिक कानून द्वारा भी बदलती है और चरण में बदलाव से आगे है। विभेदक (1.7.15), हमें त्वरण मिलता है:

1.7.2। गणितीय पेंडुलम

गणितीय पेंडुलम वे एक आदर्श प्रणाली कहते हैं जिसमें एक बेकार भार रहित धागा होता है, जिस पर शरीर को निलंबित कर दिया जाता है, जिसका पूरा द्रव्यमान एक बिंदु पर केंद्रित होता है।

समतोल स्थिति पर पेंडुलम का विचलन एक कोण द्वारा चिह्नित किया जाता है जो एक ऊर्ध्वाधर (चित्र 1.7.3) के साथ धागे द्वारा गठित एक कोण द्वारा विशेषता है।

अंजीर। 1.7.3। गणितीय पेंडुलम

संतुलन की स्थिति से पेंडुलम के विचलन के साथ, एक घूर्णन क्षण उत्पन्न होता है, जो पेंडुलम को संतुलन स्थिति में वापस करना चाहता है:

हम पेंडुलम के लिए घूर्णन गति की गतिशीलता के समीकरण के लिए लिखेंगे, यह देखते हुए कि इसकी जड़ता का क्षण एमएल 2 है:

इस समीकरण के कारण हो सकता है:

छोटे oscillations के मामले तक सीमित sinφ ≈ φ और पदनाम पेश करना:

समीकरण (1.7.1 9) को निम्नानुसार प्रस्तुत किया जा सकता है:

जो वसंत पेंडुलम में उतार-चढ़ाव के समीकरण के साथ आकार में मेल खाता है। नतीजतन, इसका समाधान एक हार्मोनिक ऑसीलेशन होगा:

(1.7.20) से यह इस प्रकार है कि गणितीय पेंडुलम के ऑसीलेशन की चक्रीय आवृत्ति इसकी लंबाई और मुक्त गिरावट के त्वरण पर निर्भर करती है। ऑसीलेशन अवधि () और (1.7.20) के लिए सूत्र का उपयोग करके, हम एक ज्ञात अनुपात प्राप्त करते हैं:

1.7.3। भौतिक पेंडुलम

भौतिक पेंडुलम कहा जाता है ठोसएक निश्चित बिंदु के आसपास ऑसीलेशन करने में सक्षम जो जड़ता के केंद्र से मेल नहीं खाता है। संतुलन स्थिति में, पेंडुलम में पेंडुलम की जड़ता एक लंबवत पर निलंबन बिंदु के नीचे है (चित्र 1.7.4)।

अंजीर। 1.7.4। भौतिक पेंडुलम

जब पेंडुलम समतोल की स्थिति से कोण तक विचलित होता है, तो एक घूर्णन क्षण उत्पन्न होता है, जो पेंडुलम को संतुलन स्थिति में वापस करना चाहता है:

जहां एम पेंडुलम का द्रव्यमान है, एल निलंबन बिंदु और पेंडुलम के जड़ता केंद्र के बीच की दूरी है।

हम पेंडुलम को घूर्णन गति की गतिशीलता के समीकरण को लिखेंगे, यह देखते हुए कि इसकी जड़ता का क्षण i के बराबर है:

छोटे oscillations के लिए sinφ ≈ φ। फिर पदनाम पेश करना:

जो वसंत पेंडुलम में उतार-चढ़ाव के समीकरण के साथ फॉर्म के साथ भी मेल खाता है। समीकरणों (1.7.27) और (1.7.26) से यह निम्नानुसार है कि संतुलन स्थिति से भौतिक पेंडुलम के छोटे विचलन के साथ, यह हार्मोनिक ऑसीलेशन बनाता है, जिसकी आवृत्ति पेंडुलम के द्रव्यमान पर निर्भर करती है, जड़ता का क्षण और रोटेशन अक्ष और जड़ता के केंद्र के बीच की दूरी। (1.7.26) के साथ, आप ऑसीलेशन की अवधि की गणना कर सकते हैं:

सूत्रों की तुलना (1.7.28) और () हमें उस गणितीय पेंडुलम को लंबाई के साथ मिलता है:

भौतिक पेंडुलम के रूप में आवेश की समान अवधि होगी। राशि (1.7.29) कहा जाता है दी गई लंबाई शारीरिक पेंडुलम। नतीजतन, भौतिक पेंडुलम की लंबाई इस तरह के गणितीय पेंडुलम की लंबाई है, जो आवेश की अवधि इस भौतिक पेंडुलम के आवेश की अवधि के बराबर है।

जड़ता के केंद्र के साथ निलंबन बिंदु को जोड़ने वाली सीधी रेखा पर बिंदु, रोटेशन की धुरी से लंबाई की लंबाई की दूरी पर झूठ बोलना, कहा जाता है सेंटर स्विंग शारीरिक पेंडुलम। स्टेनर प्रमेय पर, भौतिक पेंडुलम की जड़ता का क्षण है:

जहां मैं 0 जड़ता के केंद्र के सापेक्ष जड़ता का क्षण है। प्रतिस्थापित (1.7.30) (1.7.2 9), हमें मिलता है:

इसलिए, लंबाई की लंबाई हमेशा निलंबन बिंदु और पेंडुलम के जड़ता केंद्र के बीच की दूरी से अधिक होती है, इसलिए निलंबन बिंदु और स्विंग केंद्र जड़ता के केंद्र से अलग-अलग पक्षों पर झूठ बोलता है।

1.7.4। हार्मोनिक ऑसीलेशन की ऊर्जा

हार्मोनिक ऑसीलेशन में, अर्ध-लोचदार बल की कार्रवाई के कारण उतार-चढ़ाव वाले शरीर ई और संभावित ऊर्जा ई पी की गतिशील ऊर्जा का आवधिक पारस्परिक रूपांतरण। इन ऊर्जाओं में से, ऑसीलेटर सिस्टम की कुल ऊर्जा ई रचित है:

हम अंतिम अभिव्यक्ति को बढ़ाते हैं

लेकिन के \u003d एमω 2, इसलिए हमें ऑसीलेटरिंग बॉडी की कुल ऊर्जा के लिए एक अभिव्यक्ति मिलती है

इस प्रकार, हार्मोनिक ऑसीलेशन की कुल ऊर्जा स्थिर है और आयाम के वर्ग और दोलन की परिपत्र आवृत्ति के वर्ग के आनुपातिक है।

1.7.5। बहने वाले ऑसीलेशन .

हार्मोनिक ऑसीलेशन का अध्ययन करते समय, घर्षण और प्रतिरोध शक्तियों को वास्तविक प्रणालियों में मौजूद खाते में नहीं लिया गया था। इन बलों की कार्रवाई में आंदोलन की प्रकृति को काफी बदलाव आया, दोलन बन जाता है प्रयास करने से.

यदि प्रतिरोध बल (घर्षण बल) को छोड़कर प्रणाली, न्यूटन का दूसरा कानून सिस्टम में कार्य करता है, तो न्यूटन के दूसरे कानून को निम्नानुसार लिखा जा सकता है:

जहां आर आंदोलन का प्रतिरोध करने के लिए माध्यम के गुणों की विशेषता है, घर्षण गुणांक। सबस्टिट्यूट (1.7.34b) (1.7.34a) में:

इस फ़ंक्शन का ग्राफ़ एक ठोस वक्र 1 के चित्र 1.7.5 में दिखाया गया है, और स्ट्रोक लाइन 2 आयाम में परिवर्तन दिखाता है:

बहुत छोटे घर्षण के साथ, क्षय उत्तेजना की अवधि गैर-मुक्त तरल पदार्थ की अवधि के करीब है (1.7.35.b)

ऑसीलेशन के आयाम की कमी की गति निर्धारित होती है क्षीणन गुणांक: ग्रेटर β, मध्यम के अवरोधक प्रभाव को मजबूत और तेजी से आयाम कम हो जाता है। व्यवहार में, क्षीणन की डिग्री अक्सर विशेषता होती है क्षीणन का लघुगणि कम होनादोलनों के लगातार दो आयामों के संबंधों के प्राकृतिक लघुगणक के बराबर इस राशि को समझना, उत्तेजना की अवधि के बराबर एक अलग समय अंतराल:

;

नतीजतन, क्षीणन गुणांक और क्षीणन के लॉगरिदमिक अवलंबन काफी सरल निर्भरता हैं:

फॉर्मूला (1.7.37) से मजबूत क्षीणन के साथ यह देखा जा सकता है कि ऑसीलेशन की अवधि एक काल्पनिक मूल्य है। इस मामले में आंदोलन पहले से ही कहा जाता है अनावधिक। फॉर्म में Aperiodic आंदोलन का ग्राफ अंजीर में दिखाया गया है। 1.7.6। अशुभ और लुप्तप्राय ऑसीलेशन कहा जाता है अपना या नि: शुल्क। वे प्रारंभिक विस्थापन या प्रारंभिक गति के कारण उत्पन्न होते हैं और प्रारंभिक संचित ऊर्जा के कारण बाहरी प्रभाव की अनुपस्थिति में किए जाते हैं।

1.7.6। मजबूर आवेश। गूंज .

मजबूर उतार-चढ़ाव को उन लोगों को कहा जाता है जो आवधिक कानून में बाहरी बल की भागीदारी के साथ सिस्टम में होते हैं।

मान लीजिए कि बाहरी बल उत्पन्न करने वाला बल अर्ध-लोचदार बल और घर्षण बल को छोड़कर सामग्री बिंदु पर कार्य करता है

,

जहां एफ 0 आयाम है; ω - मजबूर बल के उतार-चढ़ाव की गोलाकार आवृत्ति। एक अंतर समीकरण (न्यूटन का दूसरा कानून) बनाएं:

,

मजबूर ऑसीलेशन (1.7.3 9) का आयाम पीढ़ी के बल के आयाम के लिए सीधे आनुपातिक है और माध्यम के क्षीणन गुणांक और अपने स्वयं के परिपत्र आवृत्तियों पर एक जटिल निर्भरता है और अपनी खुद की मजबूर आवृत्ति। यदि ω 0 और β सिस्टम के लिए दिया जाता है, तो मजबूर आवृत्तियों के आयाम में मजबूर बल की एक निश्चित कुछ आवृत्ति पर अधिकतम मूल्य होता है, जिसे बुलाया जाता है गुंजयमान.

घटना ही - ω 0 और β निर्दिष्ट के लिए अधिकतम आयाम की उपलब्धि - कहा जाता है अनुनाद।

अंजीर। 1.7.7। गूंज

अनुनाद के दौरान मजबूर ऑसीलेशन के आयाम के प्रतिरोध की अनुपस्थिति में असीम रूप से बड़ा होता है। इस मामले में, ω \u003d ω 0, यानी से बिना क्षीणन के सिस्टम में अनुनाद तब होता है जब मजबूर बल की आवृत्ति अपने स्वयं के ऑसीलेशन की आवृत्ति के साथ मेल खाता है। क्षीणन गुणांक के विभिन्न मूल्यों पर मजबूर बल की गोलाकार आवृत्ति से मजबूर आवृत्ति के आयाम की ग्राफिक निर्भरता अंजीर में दिखायी जाती है। पांच।

यांत्रिक अनुनाद उपयोगी और हानिकारक घटना दोनों हो सकता है। अनुनाद का हानिकारक प्रभाव मुख्य रूप से विनाश के कारण होता है जो इसका कारण बन सकता है। इस प्रकार, तकनीक में, विभिन्न कंपनों को देखते हुए, अनुनाद स्थितियों की संभावित घटना के लिए आवश्यक है, अन्यथा विनाश और आपदाएं हो सकती हैं। शरीर में आमतौर पर कई ऑसीलेशन आवृत्तियों होते हैं और तदनुसार, कई अनुनाद आवृत्तियों।

यदि किसी व्यक्ति के आंतरिक अंगों की क्षीणन गुणांक बड़ा नहीं होगा, तो बाहरी कंपन या ध्वनि तरंगों के प्रभाव में इन अंगों में उत्पन्न अनुनाद की घटनाएं दुखद परिणामों का कारण बन सकती हैं: अंगों का टूटना, अस्थिबंधन को नुकसान, आदि । हालांकि, मध्यम बाहरी प्रभावों पर ऐसी घटना व्यावहारिक रूप से देखी जाती है, क्योंकि जैविक प्रणालियों की क्षीणन गुणांक काफी बड़ा है। फिर भी, बाहरी यांत्रिक ऑसीलेशन की कार्रवाई के तहत अनुनाद घटना आंतरिक अंगों में होती है। इसमें, जाहिर है, मानव शरीर पर इंफ्रासाउंड उतार-चढ़ाव और कंपन के नकारात्मक प्रभावों के कारणों में से एक।

1.7.7। Autocalbania

ऐसे ऑसीलेटर सिस्टम भी हैं जो स्वयं संपत्ति ऊर्जा की आवधिक भर्ती को नियंत्रित करते हैं और इसलिए लंबे समय तक उतार-चढ़ाव कर सकते हैं।

वैकल्पिक बाहरी प्रभाव की अनुपस्थिति में किसी भी प्रणाली में मौजूद उतार-चढ़ाव को बुलाया जाता है स्व-दोलन, और सिस्टम स्वयं - स्व-ऑसीलेटर।

स्व-ऑसीलेशन की आयाम और आवृत्ति सबसे आटोकैलिबुलर सिस्टम में संपत्तियों पर निर्भर करती है, जब मजबूर आवेशों के विपरीत, वे बाहरी प्रभावों द्वारा निर्धारित नहीं होते हैं।

कई मामलों में, स्व-ऑसीलेटरिंग सिस्टम का प्रतिनिधित्व तीन मुख्य तत्वों (चित्र .1.7.8): 1) वास्तविक oscillating प्रणाली द्वारा किया जा सकता है; 2) ऊर्जा स्रोत; 3) कंपन प्रणाली में ऊर्जा प्रवाह नियामक। चैनल ऑसीलेटर सिस्टम प्रतिपुष्टि (चित्र 6) नियामक को प्रभावित करता है, इस प्रणाली के राज्य के बारे में नियामक को सूचित करता है।

एक यांत्रिक ऑटो-ऑसीलेटर सिस्टम का क्लासिक उदाहरण वह घड़ी है जिसमें पेंडुलम या बैलेंस ऑसीलेटर सिस्टम है, वसंत या उठाया gyry - ऊर्जा का स्रोत, और एंकर स्रोत से ऊर्जा प्रवाह का एक नियामक है प्रणाली।

कई जैविक प्रणालियों (दिल, फेफड़ों, आदि) आत्म-ऑसीलेटर हैं। इलेक्ट्रोमैग्नेटिक ऑटो-ऑसीलेटरिंग सिस्टम का एक विशिष्ट उदाहरण स्व-ऑसीलेशन के जेनरेटर हैं।

1.7.8। एक दिशा के oscillations के अलावा

एक ही दिशा और एक ही आवृत्ति के दो हार्मोनिक ऑसीलेशन के अतिरिक्त विचार करें:

एक्स 1 \u003d ए 1 कॉस (ω 0 टी + α 1), एक्स 2 \u003d ए 2 कॉस (ω 0 टी + α 2)।

हार्मोनिक ऑसीलेशन एक वेक्टर का उपयोग करके सेट किया जा सकता है जिसका लंबाई ऑसीलेशन के आयाम के बराबर होती है, और दिशा ओसीलेशन के प्रारंभिक चरण के बराबर कुछ अक्ष के साथ कोण बनाती है। यदि यह वेक्टर कोणीय वेग ω 0 के साथ घूमता है, तो चयनित अक्ष पर इसका प्रक्षेपण हार्मोनिक कानून द्वारा बदल जाएगा। इस पर आधारित, हम कुछ एक्सिस एक्स चुनते हैं और वैक्टर ए 1 और ए 2 (Fig.1.7.9) का उपयोग करके ऑसीलेशन की कल्पना करते हैं।

Fig.1.7.6 से यह इस प्रकार है

.

जिन योजनाओं में विमान पर वैक्टरों के रूप में आवृत्तियों को चित्रित किया जाता है उन्हें वेक्टर आरेख कहा जाता है।

फॉर्मूला 1.7.40 से निम्नानुसार है। क्या होगा यदि चरण अंतर शून्य के बराबर दोनों oscillations है, परिणामी oscillation का आयाम foldable oscillations के आयाम के योग के बराबर है। यदि फोल्ड करने योग्य ऑसीलेशन के चरणों में अंतर बराबर है, तो परिणामी ऑसीलेशन का आयाम बराबर है। यदि गणना की गई आवेश की आवृत्तियों समान नहीं हैं, तो इन उतार-चढ़ाव के अनुरूप वैक्टर घुमाएंगे अलग गति। इस मामले में, परिणामी वेक्टर परिमाण में पल्सेट करता है और गैर-स्थायी गति के साथ घूमता है। नतीजतन, इसके परिणामस्वरूप, यह एक हार्मोनिक oscillation नहीं है, बल्कि एक जटिल oscillatory प्रक्रिया।

1.7.9। बिविया

आवृत्ति में भिन्न एक ही दिशा के दो हार्मोनिक ऑसीलेशन के अतिरिक्त पर विचार करें। उनमें से एक की आवृत्ति ω के बराबर है, और दूसरा ω + δω, और δω<<ω. Положим, что амплитуды складываемых колебаний одинаковы и начальные фазы обоих колебаний равны нулю. Тогда уравнения колебаний запишутся следующим образом:

x 1 \u003d एक cos ωt, x 2 \u003d एक cos (ω + δω) टी।

इन अभिव्यक्तियों को बनाने और कोसाइन की मात्रा के लिए सूत्र का उपयोग करने के बाद, हमें मिलता है:

ऑसीलेशन (1.7.41) आवृत्ति ω के हार्मोनिक ऑसीलेशन के रूप में माना जा सकता है, जो कानून द्वारा परिवर्तन के आयाम के रूप में माना जा सकता है। यह फ़ंक्शन मॉड्यूल के संकेत के तहत अभिव्यक्ति की आवृत्ति की तुलना में दो गुना अधिक आवृत्ति के साथ आवृत्ति है, यानी आवृत्ति के साथ δω। इस प्रकार, आयाम पल्सेशन की आवृत्ति, जिसे बीट्स की आवृत्ति कहा जाता है, फोल्डबल ऑसीलेशन की आवृत्ति में अंतर के बराबर होता है।

1.7.10। परस्पर लंबवत oscillations (आंकड़े Lissuzh) के अलावा

यदि सामग्री बिंदु एक्स अक्ष के साथ और वाई की धुरी के साथ ऑसीलेशन करता है, तो यह कुछ curvilinear प्रक्षेपण के साथ आगे बढ़ जाएगा। उसी के आवृत्ति और शून्य के बराबर पहले ऑसीलेशन के प्रारंभिक चरण की आवृत्ति दें, फिर ऑसीलेशन समीकरण फॉर्म में लिखेंगे:

समीकरण (1.7.43) एक दीर्घवृत्त समीकरण है, जिनमें से कुल्हाड़ी को समन्वय अक्ष एक्स और वाई के सापेक्ष मनमाने ढंग से उन्मुख हैं। दीर्घवृत्त और इसके अर्ध-अक्षों की परिमाण का अभिविन्यास एम्पलेट्यूड्स ए और बी और चरण अंतर α पर निर्भर करता है। कुछ विशेष मामलों पर विचार करें:

यह एक दीर्घवृत्त समीकरण है, जिनमें से कुल्हाड़ी निर्देशांक की अक्षों के साथ मेल खाते हैं, और इसके अर्ध-अक्ष amplitudes (चित्र 1.7.12) के बराबर हैं। यदि आयाम बराबर हैं, तो एलिप्स एक सर्कल बन जाता है।

अंजीर .1.12

यदि पारस्परिक रूप से लंबवत ऑसीलेशन की आवृत्तियों कम मूल्य पर भिन्न होती हैं, तो उन्हें एक ही आवृत्ति के दोलन के रूप में माना जा सकता है, लेकिन धीरे-धीरे बदलते चरण अंतर के साथ। इस मामले में, ऑसीलेशन समीकरण रिकॉर्ड किए जा सकते हैं

x \u003d a cos ωt, y \u003d b cos [ωt + (δωT + α)]

और अभिव्यक्ति δωT + α को चरण अंतर के रूप में माना जाता है, धीरे-धीरे रैखिक कानून के अनुसार समय के साथ बदल रहा है। इस मामले में परिणामी आंदोलन धीरे-धीरे बदलते वक्र के साथ होता है, जो लगातार एक फॉर्म लेगा जो चरण अंतर के सभी मानों को पूरा करेगा-π से + π।

यदि पारस्परिक रूप से लंबवत ऑसीलेशन की आवृत्तियों समान नहीं हैं, परिणामी आंदोलन के प्रक्षेपण में काफी जटिल घटता की उपस्थिति है, जिसे कहा जाता है आंकड़े LISEN. उदाहरण के लिए, फोल्ड ऑसीलेशन की आवृत्तियों 1 के रूप में संबंधित हैं : 2 और चरण अंतर π / 2। फिर ऑसीलेशन समीकरण हैं

x \u003d a cos ωt, y \u003d b cos।

धुरी एक्स के साथ समय के दौरान, बिंदु एक चरम स्थिति से दूसरे स्थान पर पहुंच जाता है, एक्सिस वाई के साथ, शून्य स्थिति से बाहर आ रहा है, इसमें एक चरम स्थिति प्राप्त करने का समय है, फिर एक और और वापसी। वक्र का दृश्य अंजीर में दिखाया गया है। 1.7.13। एक ही आवृत्ति अनुपात के साथ वक्र, लेकिन चरण अंतर शून्य है Fig.1.7.14 में दिखाया गया है। गणना की आवृत्तियों की आवृत्तियों का अनुपात वापस आंकड़ों के चौराहे के अंक की संख्या का अनुपात सीधे, समन्वय की समानांतर अक्षों के साथ घूम रहा है। इसलिए, आंकड़ों के रूप में लिस्ज़ज़, आप फोल्ड करने योग्य ऑसीलेशन या अज्ञात आवृत्ति की आवृत्तियों का अनुपात निर्धारित कर सकते हैं। यदि आवृत्तियों में से एक ज्ञात है।

अंजीर .1.1.13

अंजीर .1.1.14

इकाई के करीब एक तर्कसंगत अंश आवृत्ति आवृत्ति की आवृत्ति आवृत्ति, lisitions के आंकड़ों को और अधिक कठिन।

1.7.11। एक लोचदार वातावरण में लहर वितरण

यदि किसी भी स्थान पर एक लोचदार (ठोस तरल या गैसीय) माध्यम अपने कणों के oscillations शुरू करने के लिए, तो कणों के बीच बातचीत के कारण, यह oscillation कुछ गति पर एक कण से एक कण में एक कण में एक पर्यावरण में वितरित किया जाएगा as। अंतरिक्ष में oscillations के वितरण की प्रक्रिया कहा जाता है लहर.

मध्यम कण जिनमें लहर लागू होती है, अनुवाद आंदोलन में लहर में शामिल नहीं होती है, वे केवल अपने संतुलन प्रावधानों के पास ऑसीलेशन बनाते हैं।

उस दिशा के सापेक्ष कण oscillations के क्षेत्रों के आधार पर जिसमें लहर वितरित की जाती है, प्रतिष्ठित अनुदैर्ध्य मैं आड़ा लहर की। अनुदैर्ध्य लहर में, कण माध्यम लहर के फैलाव के साथ उतार-चढ़ाव करता है। ट्रांसवर्स लहर में, मध्यम कण तरंगों के प्रचार की दिशा के लिए लंबवत दिशाओं में उतार-चढ़ाव करता है। लोचदार अनुप्रस्थ तरंगें केवल एक कतरनी प्रतिरोध के साथ एक माध्यम में हो सकती हैं। इसलिए, तरल और गैसीय मीडिया में, केवल अनुदैर्ध्य तरंगों द्वारा होना संभव है। एक ठोस माध्यम में, दोनों अनुदैर्ध्य और अनुप्रस्थ तरंगें हो सकती हैं।

अंजीर में। 1.7.12 एक अनुप्रस्थ तरंग माध्यम में वितरित किए जाने पर कणों के आंदोलन को दर्शाता है। कमरे 1.2, आदि हैं। कण एक दूसरे के पीछे (¼T) के बराबर दूरी के लिए पीछे हट रहे हैं, यानी कणों द्वारा किए गए ऑसीलेशन की अवधि के एक चौथाई के लिए एक लहर द्वारा यात्रा की गई दूरी पर। उस समय, शून्य के लिए लिया गया समय, लहर, बाएं से दाएं धुरी के साथ फैला हुआ, एक कण 1 तक पहुंच गया, जिसके परिणामस्वरूप कण बराबर की स्थिति से आगे बढ़ने लगा, निम्नलिखित कणों को आकर्षक बना दिया। कण की अवधि का एक चौथाई कण संतुलन की चरम ऊपरी स्थिति तक पहुंचता है 2. अवधि के एक और तिमाही के आने पर, पहला भाग संतुलन की स्थिति होगी, जो दिशा में ऊपर से नीचे तक जा रहा है, दूसरा कण चरम ऊपरी स्थिति तक पहुंच जाएगा, और तीसरा कण संतुलन स्थिति को स्थानांतरित करना शुरू कर देगा। समय के समय टी के बराबर, पहला कण oscillations के पूर्ण चक्र को खत्म कर देगा और एक स्पष्टीकरण के रूप में आंदोलन की स्थिति में होगा। पथ को पारित करने वाले समय तक लहर (υ), कण 5 तक पहुंच जाएगी।

अंजीर में। 1.7.13 जब अनुदैर्ध्य लहर को माध्यम में वितरित किया जाता है तो कणों के आंदोलन को दिखाता है। एक ट्रांसवर्स लहर में कणों के व्यवहार से संबंधित सभी तर्क इस मामले को भी दाईं ओर और बाएं ऑफसेट तक विस्थापन के प्रतिस्थापन के साथ भी जिम्मेदार ठहराया जा सकता है।

आकृति से यह स्पष्ट है कि जब अनुदैर्ध्य लहर का प्रचार होता है, तो वैकल्पिक सांद्रता और कण निर्वहन बनाए जाते हैं (एकाग्रता साइट को आंकड़े बिंदीदार रेखा में घुमाया जाता है), गति पर तरंग प्रसार की दिशा में आगे बढ़ते हुए।

अंजीर। 1.7.15

अंजीर। 1.7.16

अंजीर में। 1.7.15 और 1.7.16 कणों के oscillations, स्थिति, सामूहिक, जो अक्ष पर झूठ बोलता है एक्स।वास्तव में, न केवल अक्ष में स्थित कण उतार-चढ़ाव एक्सऔर कुछ मात्रा में कणों की कुलता संपन्न हुई। ऑसीलेशन के स्रोतों से फैलते हुए, लहर प्रक्रिया में अंतरिक्ष के सभी नए और नए हिस्सों को शामिल किया गया है, बिंदुओं के ज्यामितीय स्थान, जिसके लिए ओसीले समय तक पहुंचते हैं, बुलाया जाता है लहर के सामने (या लहर मोर्चा)। तरंग मोर्चा सतह का प्रतिनिधित्व करता है जो पहले से ही लहर प्रक्रिया में शामिल स्थान के हिस्से को अलग करता है, जिस क्षेत्र में ऑसीलेशन अभी तक उत्पन्न नहीं हुआ है।

बिंदुओं के ज्यामितीय स्थान, एक ही चरण में उतार-चढ़ाव, कहा जाता है तरंग सतह . तरंग की सतह को लहर प्रक्रिया द्वारा कवर किए गए किसी भी बिंदु के माध्यम से किया जा सकता है। इसलिए, लहर सतहों में एक अनंत सेट होता है, जबकि हर बार तरंग मोर्चा केवल एक ही होता है। वेव सतहें गैर-जंगम रहें (वे कणों के संतुलन की स्थिति से गुजरती हैं, एक चरण में उतार-चढ़ाव करती हैं ). वेवफ़्रंट हर समय चलता है।

तरंग सतहें कोई भी रूप हो सकती हैं। सबसे सरल मामलों में, उनके पास एक विमान या गोलाकार का एक रूप होता है। तदनुसार, इन मामलों में लहर को फ्लैट या गोलाकार कहा जाता है। एक फ्लैट लहर में, तरंग सतह एक गोलाकार लहर में एक गोलाकार लहर में एक दूसरे के विमानों के समानांतर का एक सेट है - केंद्रित क्षेत्रों की बहुलता।

अंजीर। 1.7.17

फ्लैट लहर को धुरी के साथ फैलने दें एक्स।। फिर क्षेत्र के सभी बिंदु, स्थिति, संतुलन जिसमें एक ही समन्वय होता है एक्स।(लेकिन समन्वय मूल्यों का अंतर वाईतथा जेड)उसी चरण में उतार-चढ़ाव।

अंजीर में। 1.7.17 एक वक्र को दर्शाता है जो ऑफसेट देता है ξ संतुलन की स्थिति से अलग के साथ अंक एक्स।कुछ समय पर। आपको इस पैटर्न को लहर की एक दृश्य छवि के रूप में नहीं मानना \u200b\u200bचाहिए। यह आंकड़ा कार्यों के कार्यक्रम को दर्शाता है। ξ (एक्स, टी)कुछ निश्चित के लिए समय टीइस तरह के एक कार्यक्रम को अनुदैर्ध्य और अनुप्रस्थ लहर के लिए दोनों का निर्माण किया जा सकता है।

दूरी λ, लहर थोड़े समय के लिए फैल रही है, माध्यम के कणों के ऑसीलेशन की अवधि के बराबर, कहा जाता है तरंग दैर्ध्य. यह स्पष्ट है कि

लहर की गति कहां है, टी-अवधि की अवधि। वालरो लंबी लंबाई के साथ-साथ माध्यम के निकटतम बिंदुओं के बीच की दूरी, चरण अंतर के साथ उतार-चढ़ाव, 2π के बराबर (चित्र 1.7.14 देखें)

1 / ν (ν - आवृत्ति की आवृत्ति) के माध्यम से अनुपात (1.7.45) टी में बदलना, हम प्राप्त करते हैं

यह सूत्र निम्नलिखित विचारों से भी आ सकता है। एक सेकंड में, तरंगों का स्रोत ν ऑसीलेशन करता है, प्रत्येक ऑसीलेशन एक "कंघी" और एक "लहर" तरंगों के साथ माध्यम में उत्पन्न करता है। तब तक जब स्रोत ν - ई उतार-चढ़ाव को पूरा करता है, तो पहले "comb" के पास पथ को पारित करने का समय होगा as। नतीजतन, "लकीरें" और "वीपैडिन" तरंगों को की लंबाई में पूरा किया जाना चाहिए।

1.7.12। फ्लैट तरंग समीकरण

तरंग समीकरण को एक अभिव्यक्ति कहा जाता है जो अपने निर्देशांक के कार्य के रूप में oscillating कण के विस्थापन देता है एक्स, वाई, जेड और समय टी :

ξ \u003d ξ (x, y, z; t)

(कण की संतुलन स्थिति के निर्देशांक को ध्यान में रखते हुए हैं)। यह सुविधा समय के बारे में आवधिक होना चाहिए टी , और निर्देशांक के सापेक्ष एक्स, वाई, जेड। । समय में आवधिकता इस तथ्य से होती है कि अंक जो एक दूसरे से दूरी पर अलग होते हैं λ , उसी तरह उतार-चढ़ाव।

फ़ंक्शन का एक रूप खोजें ξ एक सपाट लहर के मामले में, यह मानते हुए कि oscillations सामंजस्यपूर्ण हैं। सरल बनाने के लिए, निर्देशांक की धुरी भेजें ताकि अक्ष हो सके एक्स। तरंग प्रचार की दिशा के साथ मेल खाता है। फिर लहर की सतह एक्सिस के लिए लंबवत होगी एक्स। और, चूंकि लहर की सतह के सभी बिंदु समान रूप से, ऑफसेट हैं ξ केवल इस पर निर्भर करेगा एक्स। तथा टी:

ξ = ξ (x, टी) .

अंजीर .1.1.18

विमान में झूठ बोलने वाले बिंदुओं के दोलन को दें एक्स। = 0 (चित्र 1.7.18), हैं

मनमाने ढंग से मूल्य के अनुरूप विमान में अंकों के oscillation का प्रकार खोजें एक्स। । ताकि विमान से मार्ग पारित किया जा सके एक्स।=0 इस विमान से पहले, लहर में समय लगता है ( υ - लहर के फैलाव का आवरण)। नतीजतन, विमान में झूठ बोलने वाले कणों के दोलन एक्स। समय पर अंतराल होगा τ विमान में कण oscillations से एक्स। = 0 । दिखाई देगा

इसलिए, फ्लैट तरंग समीकरण (अनुदैर्ध्य, और अनुप्रस्थ), धुरी की दिशा में प्रचार एक्स। , निम्नलिखित नुसार:

यह अभिव्यक्ति टी के बीच संबंध निर्धारित करती है और जगह एक्स। जिसमें चरण में एक निश्चित मूल्य होता है। परिणामी DX / DT मान गति देता है जिसके साथ यह चरण मान चलता है। आक्रामक अभिव्यक्ति (1.7.48), हमें मिलता है

उतरने की ओर बढ़ने वाली लहर का समीकरण एक्स। :

फॉर्मूला (1.7.53) के समापन में, हमने माना कि ऑसीलेशन का आयाम निर्भर नहीं करता है एक्स। । एक सपाट लहर के लिए, इस मामले में यह देखा जाता है जब तरंग ऊर्जा माध्यम से अवशोषित नहीं होती है। जब ऊर्जा को अवशोषित करने में वितरित किया जाता है, तो ऑसीलेशन के स्रोत से हटाने के साथ लहर की तीव्रता धीरे-धीरे घट रही है - लहर क्षीण हो रही है। अनुभव से पता चलता है कि एक सजातीय माध्यम में इस तरह के क्षीणन घातीय कानून में होता है:

क्रमश: फ्लैट लहर समीकरण, खाता क्षीणन में लेइसमें निम्नलिखित रूप हैं:

(एक 0 - विमान X \u003d 0 के बिंदुओं पर आयाम)।