สูตรของพลังงานเชิงกลที่สมบูรณ์ของลูกตุ้มฤดูใบไม้ผลิที่ผันผวน การแกว่งฟรี ลูกตุ้มฤดูใบไม้ผลิ นิยามลูกตุ้มฤดูใบไม้ผลิ

คำนิยาม 1.

การแกว่งฟรีสามารถทำได้ภายใต้การกระทำของกองกำลังภายในหลังจากลบออกจากตำแหน่งสมดุลของระบบทั้งหมด

เพื่อให้ oscillates ทำตามกฎหมายฮาร์มอนิกเป็นสิ่งจำเป็นที่แรงที่ส่งคืนร่างกายเข้าไปในตำแหน่งสมดุลเป็นสัดส่วนกับอคติจากตำแหน่งสมดุลและถูกนำไปที่ด้านข้างตรงข้ามกับการกระจัดกระจาย

f (t) \u003d m a (t) \u003d - m ω 2 x (t)

อัตราส่วนชี้ให้เห็นว่าωคือความถี่ของการสั่นฮาร์มอนิก คุณสมบัตินี้เป็นลักษณะของแรงยืดหยุ่นภายในการบังคับใช้กฎหมาย Dungal:

f u p p \u003d - k x

นิยาม 2.

กองกำลังของธรรมชาติใด ๆ ที่ตอบสนองเงื่อนไขที่เรียกว่า กึ่งยืดหยุ่น.

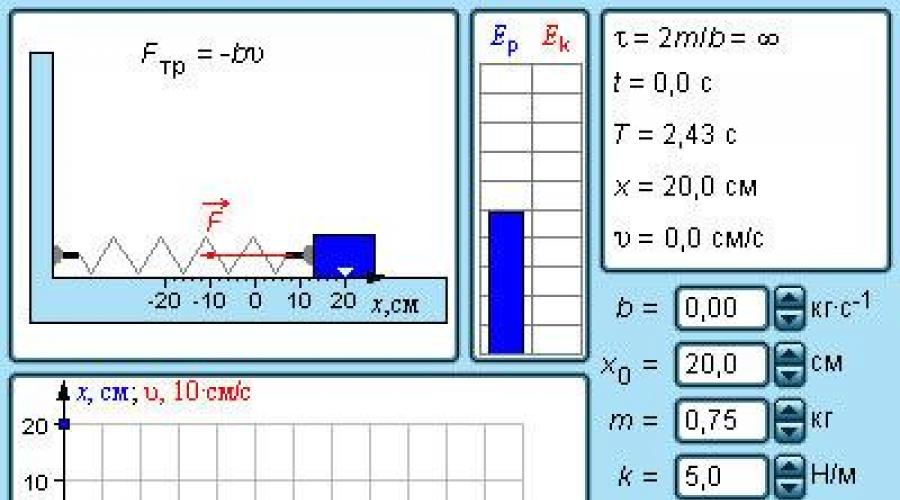
นั่นคือโหลดที่มีมวล m ซึ่งแนบมากับสปริง K ที่มีปลายที่แสดงในรูปที่ 2 2. 1, ทำขึ้นของระบบที่มีความสามารถในการดำเนินการออแกนิกอิสระในกรณีที่ไม่มีแรงเสียดทาน

นิยาม 3.

การขนส่งสินค้าตั้งอยู่ในฤดูใบไม้ผลิเรียกว่า oscillator ฮาร์มอนิกเชิงเส้น

ภาพ 2 . 2 . 1 . การแกว่งขนส่งสินค้าในฤดูใบไม้ผลิ ไม่มีแรงเสียดทาน

ความถี่วงกลม

รากฐานของความถี่วงกลมω 0 ทำโดยใช้สูตรของกฎหมายที่สองของนิวตัน:

m a \u003d - k x \u003d m ω 0 2 x

ดังนั้นเราจะได้รับ:

คำนิยาม 4.

ความถี่ω 0 เรียกว่า ความถี่ของตัวเองของระบบ oscillatory.

การกำหนดระยะเวลาของการสั่นสะเทือนฮาร์มอนิคของสินค้าในฤดูใบไม้ผลิ t มาจากสูตร:

t \u003d 2 πω 0 \u003d 2 π m k

ตำแหน่งแนวนอนของระบบขนส่งสินค้าฤดูใบไม้ผลิแรงโน้มถ่วงได้รับการชดเชยด้วยพลังของปฏิกิริยาการสนับสนุน เมื่อแขวนสินค้าในฤดูใบไม้ผลิทิศทางของแรงโน้มถ่วงจะไปตามสายการไหลของสินค้า ตำแหน่งดุลยภาพของสปริงยืดคือ:

x 0 \u003d m g k ในขณะที่การแกว่งดำเนินการใกล้กับสภาวะสมดุลใหม่ สูตรของความถี่ของตัวเองω 0 และระยะเวลาการแกว่ง T ในการแสดงออกด้านบนมีความยุติธรรม

คำนิยาม 5.

กับการเชื่อมต่อทางคณิตศาสตร์ที่มีอยู่ระหว่างการเร่งความเร็วของร่างกาย A และพิกัดพฤติกรรมของระบบออสซิลโล่โดดเด่นด้วยคำอธิบายที่เข้มงวด: การเร่งความเร็วเป็นอนุพันธ์ที่สองของพิกัดของร่างกาย x ตามเวลา T:

คำอธิบายของกฎหมายที่สองของนิวตันกับสินค้าในฤดูใบไม้ผลิจะถูกบันทึกเป็น:

m a - m x \u003d - k x, หรือ x ¨ + ω 0 2 x \u003d 0 ซึ่งความถี่ฟรีω 0 2 \u003d k m

หากระบบทางกายภาพขึ้นอยู่กับสูตร X ¨ + ω 0 2 x \u003d 0 จากนั้นพวกเขาสามารถดำเนินการเคลื่อนไหวฮาร์มอนิกออสซิลเลตได้ฟรีพร้อมแอมพลิจูดที่แตกต่างกัน นี่เป็นไปได้เนื่องจาก x \u003d x m cos ใช้ (ω t + φ 0)

สมการของแบบฟอร์ม x ¨ + ω 0 2 x \u003d 0 ได้รับชื่อ สมการของการแกว่งฟรี. พวกเขา สมบัติทางกายภาพ เพียงความถี่การสั่นของตัวเองω 0 หรือระยะเวลาของ T

แอมพลิจูด X M และเฟสเริ่มต้นφ 0 พบวิธีที่ได้รับจากสถานะสมดุลของเวลาเริ่มต้น

ตัวอย่างที่ 1

ในการปรากฏตัวของสินค้าที่พลัดถิ่นจากตำแหน่งสมดุลระยะทางδ l และช่วงเวลาของเวลาเท่ากับ t \u003d 0 มันจะลดลงโดยไม่มีความเร็วเริ่มต้น จากนั้น x m \u003d δ l, φ 0 \u003d 0 หากภาระอยู่ในตำแหน่งสมดุลความเร็วเริ่มต้น±υ 0 จะถูกส่งเมื่อส่งสัญญาณเริ่มต้นจากที่นี่ x m \u003d m k υ 0, φ 0 \u003d ±π 2

แอมพลิจูด X M ที่มีเฟสเริ่มต้นφ 0 ถูกกำหนดโดยการปรากฏตัวของเงื่อนไขเริ่มต้น

รูปที่ 2 2. 2. รูปแบบของการแกว่งขนส่งสินค้าฟรีในฤดูใบไม้ผลิ

ระบบออสซิลเลโต้เชิงกลนั้นโดดเด่นด้วยการปรากฏตัวของการเปลี่ยนรูปแบบยืดหยุ่นในแต่ละอัน รูปที่ 2 2. 2 แสดงมุมอะนาล็อกของ oscillator ฮาร์มอนิกซึ่งทำให้การสั่นสะเทือน ดิสก์แขวนอยู่ในแนวนอนบนด้ายยืดหยุ่นที่แนบมาในศูนย์กลางของมวล ถ้ามันถูกหมุนไปที่มุมθจากนั้นช่วงเวลาของแรงของการเสียรูปแบบยืดหยุ่นของการบิด m y p p p:

m y p p \u003d - x θ

การแสดงออกนี้ไม่สอดคล้องกับกฎหมายของลำคอสำหรับการเสียรูปของการบิด ค่าของ x คล้ายกับความแข็ง K ของฤดูใบไม้ผลิ บันทึกของกฎหมายที่สองของนิวตันสำหรับการเคลื่อนที่แบบหมุนของดิสก์ใช้เวลา

i ε \u003d m y p p \u003d - x θหรือθ¨ \u003d - x θซึ่งช่วงเวลาของความเฉื่อยจะถูกแสดงโดย i \u003d i c และεเป็นความเร่งเชิงมุม

ในทำนองเดียวกันกับสูตรลูกตุ้มฤดูใบไม้ผลิ:

ω 0 \u003d x i, t \u003d 2 π i x.

การใช้ลูกตุ้มแบบบิดนั้นสังเกตได้ในนาฬิกาเชิงกล เขาได้ชื่อของ Balancer ซึ่งการสร้างช่วงเวลาของแรงยืดหยุ่นจะดำเนินการโดยใช้สปริงรูปเกลียว

รูปที่ 2 2. 3. ลูกตุ้มเย็น

หากคุณสังเกตเห็นข้อผิดพลาดในข้อความโปรดเลือกและกด CTRL + ENTER

ลูกตุ้มฤดูใบไม้ผลิเป็นระบบออสซิลเลชั่นที่ประกอบด้วยจุดวัสดุที่มีน้ำหนักและสปริง พิจารณาลูกตุ้มฤดูใบไม้ผลิแนวนอน (รูปที่ 1, A) มันเป็นร่างกายขนาดใหญ่ที่เจาะตรงกลางและวางบนก้านแนวนอนซึ่งสามารถเลื่อนได้โดยไม่มีแรงเสียดทาน (ระบบออสซิลเลสในอุดมคติ) ก้านได้รับการแก้ไขระหว่างการรองรับแนวตั้งสองแนว

สปริงที่ทนต่อเจ้าสาวติดอยู่กับร่างกายที่ปลายด้านหนึ่ง ปลายอีกด้านของการสิ้นสุดได้รับการแก้ไขในการสนับสนุนซึ่งในกรณีที่ง่ายที่สุดคือความสงบสุขเกี่ยวกับระบบอ้างอิงเฉื่อยซึ่งการแกว่งของลูกตุ้มเกิดขึ้น ที่จุดเริ่มต้นของฤดูใบไม้ผลิไม่ได้เปลี่ยนรูปและร่างกายอยู่ในตำแหน่งสมดุลของ C ถ้ายืดหรือบีบฤดูใบไม้ผลินำร่างกายออกจากตำแหน่งสมดุลจากนั้นพลังของความยืดหยุ่นจะเริ่มต้นที่ด้านข้างของ ฤดูใบไม้ผลิที่เสียรูปพลังของความสมดุลจะเริ่มขึ้น

ปล่อยให้เราบีบฤดูใบไม้ผลิขยับร่างกายไปยังตำแหน่ง A และปล่อยให้ไป ภายใต้การกระทำของความแข็งแกร่งของความยืดหยุ่นมันจะเคลื่อนที่เร่ง ในเวลาเดียวกันแรงสูงสุดของความยืดหยุ่นนั้นใช้ได้กับร่างกายเนื่องจากมีการยืดตัวที่แท้จริงของ X M Springs ที่ใหญ่ที่สุด ดังนั้นในตำแหน่งนี้การเร่งความเร็วสูงสุด เมื่อร่างกายเคลื่อนไปยังตำแหน่งของความสมดุลส่วนขยายที่สมบูรณ์ของฤดูใบไม้ผลิลดลงและดังนั้นการเร่งความเร็วจะลดลงรายงานโดยความยืดหยุ่นโดยแรง แต่เนื่องจากการเร่งความเร็วในการเคลื่อนไหวนี้จะเคลือบด้วยความเร็วความเร็วของลูกตุ้มเพิ่มขึ้นและในตำแหน่งดุลยภาพมันจะเป็นสูงสุด

เมื่อถึงตำแหน่งของความสมดุล C ร่างกายจะไม่หยุด (แม้ว่าฤดูใบไม้ผลิจะไม่เปลี่ยนรูปในตำแหน่งนี้และความแข็งแกร่งของความยืดหยุ่นเป็นศูนย์) และมีความเร็วจะเคลื่อนที่ด้วยความเฉื่อยยืดสปริง ตอนนี้แรงของความยืดหยุ่นที่เกิดขึ้นใหม่นั้นมุ่งเน้นไปที่การเคลื่อนไหวของร่างกายและช้าลง ที่จุด D ความเร็วของร่างกายจะเป็นศูนย์และการเร่งความเร็วสูงสุดร่างกายจะหยุดสักครู่หลังจากที่ความยืดหยุ่นจะเริ่มเคลื่อนไหวในทิศทางตรงกันข้ามกับตำแหน่งของสมดุล การกระทำของเขาโดยความเฉื่อยร่างกายบีบสปริงและชะลอการเคลื่อนไหวถึงจุด A (เนื่องจากไม่มีแรงเสียดทาน), I.e. ครบวงจรเต็ม หลังจากนั้นการเคลื่อนไหวของร่างกายจะถูกทำซ้ำในลำดับที่อธิบายไว้ ดังนั้นเหตุผลของการแกว่งฟรีของลูกตุ้มฤดูใบไม้ผลิจึงเป็นผลของแรงของความยืดหยุ่นที่เกิดขึ้นระหว่างการเปลี่ยนรูปของฤดูใบไม้ผลิและความเฉื่อยของร่างกาย

ตามกฎหมายของลำคอ f x \u003d -kx ตามกฎหมายที่สองของนิวตัน F X \u003d Ma X ดังนั้น ma x \u003d -kx จากที่นี่

สมการแบบไดนามิกของการเคลื่อนไหวลูกตุ้มสปริง

เราเห็นว่าการเร่งความเร็วกำลังเคลื่อนย้ายโดยตรงและตรงข้ามถูกนำไปตรงมา การเปรียบเทียบสมการที่ได้รับด้วยสมการการสั่นฮาร์มอนิก เราเห็นว่าลูกตุ้มฤดูใบไม้ผลิดำเนินการสั่นฮาร์มอนิกด้วยความถี่ของวงจร

ช่วงเวลาของการแกว่งของลูกตุ้มฤดูใบไม้ผลิ

ในสูตรเดียวกันระยะเวลาของการแกว่งของลูกตุ้มฤดูใบไม้ผลิแนวตั้งสามารถคำนวณได้ (รูปที่ 1. b) แน่นอนในตำแหน่งดุลยภาพเนื่องจากการกระทำของแรงโน้มถ่วงฤดูใบไม้ผลิจะถูกยืดออกไปยังค่าที่แน่นอนของ x 0 ซึ่งกำหนดโดยอัตราส่วน MG \u003d KX 0 เมื่อลูกตุ้มแสดงตำแหน่งดุลยภาพ o บนการฉาย X ของแรงยืดหยุ่น

หากคุณย้ายลูกบอลออกจากตำแหน่งสมดุลที่ระยะทาง x จากนั้นส่วนขยายของสปริงจะเท่ากับδl 0 + x จากนั้นแรงที่เกิดขึ้นจะใช้ค่า:

พิจารณาสภาวะสมดุล (1.7.1) เราได้รับ:

เครื่องหมาย "ลบ" แสดงให้เห็นว่าการกระจัดและพลังงานมีทิศทางตรงกันข้าม

ความแข็งแรงยืดหยุ่น F มีคุณสมบัติดังต่อไปนี้:

1. มันเป็นสัดส่วนกับการกระจัดของลูกบอลจากตำแหน่งดุลยภาพ;
2. มันมักจะนำไปสู่ตำแหน่งสมดุล

ในการแจ้งให้ระบบการกระจัด X คุณต้องทำงานกับความแข็งแกร่งของความยืดหยุ่น:

งานนี้ไปสร้างสต็อกของระบบพลังงานที่มีศักยภาพ:

ภายใต้การกระทำของความแข็งแรงของความยืดหยุ่นลูกบอลจะย้ายไปที่ตำแหน่งของความสมดุลด้วยความเร็วที่เพิ่มขึ้นเรื่อย ๆ ดังนั้นพลังงานที่มีศักยภาพของระบบจะลดลง แต่พลังงานจลน์เพิ่มขึ้น (ชั่งน้ำหนักน้ำพุละเลย) มาถึงตำแหน่งสมดุลลูกบอลจะดำเนินการต่อไปโดยความเฉื่อย นี่คือการเคลื่อนไหวช้าและหยุดเมื่อพลังงานจลน์ผ่านไปสู่ศักยภาพอย่างสมบูรณ์ จากนั้นกระบวนการเดียวกันจะไหลเมื่อลูกบอลเคลื่อนที่ไปในทิศทางตรงกันข้าม หากไม่มีแรงเสียดทานในระบบลูกบอลจะผันผวนเป็นเวลานาน

สมการของกฎหมายที่สองของนิวตันในกรณีนี้มีรูปแบบ:

เราเปลี่ยนสมการเช่นนี้:

เข้าสู่การกำหนดเราได้รับสมการเชิงอนุพันธ์เชิงเส้นที่เป็นเนื้อเดียวกันเชิงเส้น:

การทดแทนโดยตรงนั้นง่ายต่อการตรวจสอบให้แน่ใจว่าโซลูชันทั่วไปของสมการ (1.7.8) มีรูปแบบ:

ที่ A คือแอมพลิจูดและφ - ขั้นตอนแรกของการแกว่ง - ค่าถาวร ดังนั้นความผันผวนของลูกตุ้มฤดูใบไม้ผลิจึงกลมกลืนกัน (รูปที่ 1.7.2)

รูปที่. 1.7.2 การสั่นฮาร์มอนิก

เนื่องจากเป็นระยะ ๆ ของโคไซน์รัฐต่าง ๆ ของระบบออสซิลโล่จะทำซ้ำหลังจากระยะเวลาหนึ่ง (ช่วงเวลาของการสั่น) t ซึ่งซึ่งเฟสการแกว่งได้รับการเพิ่มขึ้น2π คำนวณระยะเวลาโดยใช้ความเสมอภาค:

จากที่ต่อไปนี้:

จำนวนการแกว่งต่อหน่วยเวลาเรียกว่าความถี่:

ความถี่ของการแกว่งดังกล่าวจะถูกนำมาใช้ต่อหน่วยความถี่ระยะเวลาที่เป็น 1 วินาที หน่วยดังกล่าวเรียกว่า 1 Hz

จาก (1.7.11) มันเป็นไปตาม:

ดังนั้นω 0 คือจำนวนของการแกว่งที่ดำเนินการใน2πวินาที ค่าของω 0 เรียกว่าความถี่วงกลมหรือวงจร ใช้ (1.7.12) และ (1.7.13), เขียน:

ความแตกต่าง () ในเวลาที่เราได้รับการแสดงออกความเร็วของลูกบอล:

จาก (1.7.15) มันเป็นไปตามที่ความเร็วในการเปลี่ยนแปลงของกฎหมายฮาร์มอนิกและอยู่ข้างหน้าของการเปลี่ยนแปลงในระยะด้วย½π ความแตกต่าง (1.7.15), เราได้รับการเร่งความเร็ว:

1.7.2 ลูกตุ้มคณิตศาสตร์

ลูกตุ้มคณิตศาสตร์ พวกเขาเรียกระบบในอุดมคติที่ประกอบด้วยด้ายไร้น้ำหนักที่ไม่เป็นทางการซึ่งร่างกายถูกระงับซึ่งเป็นมวลทั้งหมดที่มีความเข้มข้นจนถึงจุดหนึ่ง

การเบี่ยงเบนของลูกตุ้มในตำแหน่งดุลยภาพนั้นโดดเด่นด้วยมุมφที่เกิดขึ้นจากเธรดที่มีแนวตั้ง (รูปที่ 1.7.3)

รูปที่. 1.7.3 ลูกตุ้มคณิตศาสตร์

ด้วยการเบี่ยงเบนของลูกตุ้มจากตำแหน่งสมดุลช่วงเวลาการหมุนเกิดขึ้นซึ่งพยายามที่จะคืนลูกตุ้มไปยังตำแหน่งสมดุล:

เราจะเขียนสำหรับลูกตุ้มสมการของพลวัตของการเคลื่อนไหวการหมุนเนื่องจากช่วงเวลาของความเฉื่อยของมันคือ ML 2:

สมการนี้อาจเกิดจาก:

จำกัด เฉพาะกรณีของการแกว่งขนาดเล็กSinφ≈φและแนะนำการกำหนด:

สมการ (1.7.19) อาจนำเสนอดังนี้

ซึ่งเกิดขึ้นพร้อมกับสมการของความผันผวนในลูกตุ้มฤดูใบไม้ผลิ ดังนั้นการแก้ปัญหาของมันจะเป็นการสั่นของฮาร์มอนิก:

จาก (1.7.20) มันเป็นไปตามความถี่ของการแกว่งของการแกว่งของลูกตุ้มคณิตศาสตร์ขึ้นอยู่กับความยาวและการเร่งความเร็วของการตกฟรี การใช้สูตรสำหรับระยะเวลาการแกว่ง () และ (1.7.20) เราได้รับอัตราส่วนที่ทราบ:

1.7.3 ลูกตุ้มทางกายภาพ

ลูกตุ้มทางกายภาพเรียกว่า ของแข็งความสามารถในการดำเนินการแกว่งรอบจุดคงที่ที่ไม่ตรงกับจุดศูนย์กลางความเฉื่อย ในตำแหน่งดุลยภาพความเฉื่อยของลูกตุ้มในลูกตุ้มอยู่ภายใต้จุดช่วงล่างในแนวตั้งหนึ่ง (รูปที่ 1.7.4)

รูปที่. 1.7.4 ลูกตุ้มทางกายภาพ

เมื่อลูกตุ้มเบี่ยงเบนจากตำแหน่งดุลยภาพไปจนถึงมุมφช่วงเวลาการหมุนเกิดขึ้นซึ่งพยายามที่จะคืนลูกตุ้มไปยังตำแหน่งสมดุล:

ที่ M คือมวลของลูกตุ้ม L คือระยะห่างระหว่างจุดช่วงล่างและศูนย์กลางความเฉื่อยของลูกตุ้ม

เราจะเขียนถึงลูกตุ้มสมการของพลวัตของการเคลื่อนไหวแบบหมุนเนื่องจากช่วงเวลาของความเฉื่อยของมันเท่ากับฉัน:

สำหรับการแกว่งขนาดเล็กSinφ≈φ จากนั้นแนะนำการกำหนด:

ซึ่งสอดคล้องกับรูปแบบที่มีสมการของความผันผวนในลูกตุ้มสปริง จากสมการ (1.7.27) และ (1.7.26) ตามด้วยการเบี่ยงเบนขนาดเล็กของลูกตุ้มทางกายภาพจากตำแหน่งดุลยภาพมันทำให้การสั่นของฮาร์มอนิคความถี่ที่ขึ้นอยู่กับมวลของลูกตุ้มช่วงเวลาแห่งความเฉื่อยและ ระยะห่างระหว่างแกนหมุนและจุดศูนย์กลางของความเฉื่อย ด้วย (1.7.26) คุณสามารถคำนวณระยะเวลาของการแกว่ง:

เปรียบเทียบสูตร (1.7.28) และ () เราได้รับลูกตุ้มคณิตศาสตร์ที่มีความยาว:

จะมีช่วงเวลาเดียวกันของการแกว่งว่าเป็นลูกตุ้มทางกายภาพที่พิจารณา จำนวนเงิน (1.7.29) เรียกว่า ความยาวที่กำหนด ลูกตุ้มทางกายภาพ ดังนั้นความยาวของลูกตุ้มทางกายภาพคือความยาวของลูกตุ้มทางคณิตศาสตร์ดังกล่าวช่วงเวลาของการแกว่งซึ่งเท่ากับช่วงเวลาของการแกว่งของลูกตุ้มทางกายภาพนี้

จุดบนเส้นตรงที่เชื่อมต่อจุดช่วงล่างกับจุดศูนย์กลางของความเฉื่อยนอนอยู่ที่ระยะทางของความยาวของความยาวจากแกนของการหมุนเรียกว่า สวิงกลาง ลูกตุ้มทางกายภาพ ในทฤษฎีบท Steiner ช่วงเวลาของความเฉื่อยของลูกตุ้มทางกายภาพคือ:

ที่ฉัน 0 คือช่วงเวลาของความเฉื่อยเมื่อเทียบกับศูนย์กลางของความเฉื่อย การแทนที่ (1.7.30) ใน (1.7.29), เราได้รับ:

ดังนั้นความยาวของความยาวจึงยิ่งใหญ่กว่าระยะห่างระหว่างจุดช่วงล่างและศูนย์กลางความเฉื่อยของลูกตุ้มดังนั้นจุดช่วงล่างและศูนย์สวิงจึงอยู่ด้านต่าง ๆ จากศูนย์กลางของความเฉื่อย

1.7.4 พลังงานของการแกว่งฮาร์มอนิก

ในการสั่นฮาร์มอนิกการแปลงร่วมกันเป็นระยะ ๆ ของพลังงานจลน์ของร่างกายที่ผันผวน E เพื่อและพลังงานที่มีศักยภาพ E P เนื่องจากการกระทำของแรงที่มีความยืดหยุ่นเสมือน ของพลังงานเหล่านี้พลังงานทั้งหมดของระบบ oscillatory ประกอบด้วย:

เรายกระดับการแสดงออกครั้งสุดท้าย

แต่ k \u003d mω 2 ดังนั้นเราจึงได้รับการแสดงออกสำหรับพลังงานทั้งหมดของร่างกายสั่น

ดังนั้นพลังงานทั้งหมดของการแกว่งความกลมกลืนจึงคงที่และเป็นสัดส่วนกับสแควร์ของแอมพลิจูดและสี่เหลี่ยมจัตุรัสของความถี่แบบวงกลมของการแกว่ง

1.7.5 การแกว่งไหล .

เมื่อศึกษาการแกว่งฮาร์มอนิกแรงเสียดทานและความต้านทานไม่ได้นำมาใช้ในบัญชีที่มีอยู่ในระบบจริง การกระทำของกองกำลังเหล่านี้เปลี่ยนแปลงธรรมชาติของการเคลื่อนไหวอย่างมีนัยสำคัญการแกว่งกลายเป็น การพยายาม.

หากระบบยกเว้นแรงต้านทาน (แรงเสียดทาน) กฎหมายที่สองของการกระทำของนิวตันในระบบแล้วกฎหมายที่สองของนิวตันสามารถเขียนได้ดังนี้:

โดยที่ R คือค่าสัมประสิทธิ์แรงเสียดทานลักษณะคุณสมบัติของสื่อในการต้านทานการเคลื่อนไหว ทดแทน (1.7.34b) ใน (1.7.34a):

กราฟของฟังก์ชั่นนี้แสดงในรูปที่ 1.7.5 ของเส้นโค้งที่เป็นของแข็ง 1 และสายจังหวะ 2 แสดงการเปลี่ยนแปลงในแอมพลิจูด:

ด้วยแรงเสียดทานที่เล็กมากช่วงเวลาของการสลายตัวของการสลายตัวอยู่ใกล้กับระยะเวลาของการสั่นของเหลวที่ไม่ใช่อิสระ (1.7.35.b)

ความเร็วของการลดลงของแอมพลิจูดของการสั่น สัมประสิทธิ์การลดทอน: ยิ่งβ, ผลการยับยั้งที่แข็งแกร่งของสื่อและยิ่งแอมพลิจูดเร็วขึ้น ในทางปฏิบัติระดับของการลดทอนมักเป็นลักษณะ ลอการิทึมลดการลดทอนการทำความเข้าใจกับจำนวนนี้เท่ากับลอการิทึมตามธรรมชาติของความสัมพันธ์ของแอมพลิจูดสองต่อเนื่องกันของการแกว่ง, ช่วงเวลาที่แยกจากกันเท่ากับระยะเวลาของการแกว่ง:

;

ดังนั้นสัมประสิทธิ์การลดทอนและการลดทอนการลดทอนลอการิทึมจึงค่อนข้างพึ่งพาเรียบง่าย:

ด้วยการลดทอนที่แข็งแกร่งจากสูตร (1.7.37) จะเห็นได้ว่าระยะเวลาของการสั่นเป็นค่าจินตภาพ การเคลื่อนไหวในกรณีนี้เรียกว่าแล้ว aperiodic. กราฟของการเคลื่อนไหว aperiodic ในรูปแบบจะแสดงในรูปที่ 1.7.6 เรียกว่าการสั่นสะเทือนและซีดจาง ของตัวเอง หรือ ฟรี. พวกเขาเกิดขึ้นเนื่องจากการกระจัดเริ่มต้นหรือความเร็วเริ่มต้นและดำเนินการในกรณีที่ไม่มีอิทธิพลจากภายนอกเนื่องจากพลังงานที่สะสมในขั้นต้น

1.7.6 การแกว่งที่ถูกบังคับ เสียงสะท้อน .

ถูกบังคับ ความผันผวนนั้นเรียกว่าสิ่งที่เกิดขึ้นในระบบที่มีการมีส่วนร่วมของแรงภายนอกที่แตกต่างกันในกฎหมายกำหนด

สมมติว่าแรงที่สร้างแรงภายนอกทำหน้าที่ในจุดวัสดุยกเว้นแรงที่มีความยืดหยุ่นเสมือนและแรงเสียดทาน

,

โดยที่ f 0 เป็นแอมพลิจูด; ω - ความถี่วงกลมของความผันผวนของแรงบังคับ ทำสมการเชิงอนุพันธ์ (กฎหมายที่สองของนิวตัน):

,

แอมพลิจูดของการสั่นที่ถูกบังคับ (1.7.39) เป็นสัดส่วนโดยตรงกับแอมพลิจูดของแรงรุ่นและมีการพึ่งพาที่ซับซ้อนเกี่ยวกับสัมประสิทธิ์การลดทอนของสื่อและความถี่วงกลมของการสั่นของตัวเองและบังคับ หากได้รับω 0 และβสำหรับระบบแอมพลิจูดของการสืบค้นที่ถูกบังคับมีค่าสูงสุดที่ความถี่บางอย่างของแรงบังคับที่เรียกว่า ก้อง.

ปรากฏการณ์ของตัวเอง - ความสำเร็จของแอมพลิจูดสูงสุดสำหรับω 0 และβที่ระบุ - เรียกว่า เสียงสะท้อน

รูปที่. 1.7.7 เสียงสะท้อน

ในกรณีที่ไม่มีความต้านทานต่อแอมพลิจูดของการแกว่งที่ถูกบังคับในระหว่างเสียงสะท้อนนั้นมีขนาดใหญ่อย่างไม่สิ้นสุด ในกรณีนี้จากω \u003d ω 0, i.e. เสียงสะท้อนในระบบที่ไม่มีการลดทอนเกิดขึ้นเมื่อความถี่ของแรงบังคับให้เกิดขึ้นพร้อมกับความถี่ของการแกว่งของตัวเอง การพึ่งพากราฟิกของแอมพลิจูดของการสยองบังคับจากความถี่แบบวงกลมของแรงบังคับที่ค่าที่แตกต่างกันของสัมประสิทธิ์การลดทอนจะแสดงในรูปที่ ห้า.

เสียงสะท้อนทางกลสามารถเป็นปรากฏการณ์ที่เป็นประโยชน์และเป็นอันตราย ผลกระทบที่เป็นอันตรายของการซ้ำซ้อนส่วนใหญ่เกิดจากการทำลายที่อาจทำให้เกิด ดังนั้นในเทคนิคเนื่องจากการสั่นสะเทือนที่แตกต่างกันมีความจำเป็นต้องให้สำหรับการเกิดขึ้นของสภาพที่เป็นไปได้ของโรคเรโซแนนต์มิฉะนั้นการทำลายและภัยพิบัติอาจเป็นไปได้ ร่างกายมักจะมีความถี่การแกว่งหลายครั้งและตามความถี่พ้องหลายครั้ง

หากค่าสัมประสิทธิ์การลดทอนของอวัยวะภายในของบุคคลจะไม่ใหญ่ปรากฏการณ์เรโซแนนที่เกิดขึ้นในอวัยวะเหล่านี้ภายใต้อิทธิพลของการสั่นสะเทือนภายนอกหรือคลื่นเสียงอาจนำไปสู่ผลกระทบที่น่าเศร้า: การแตกของอวัยวะความเสียหายต่อเอ็น ฯลฯ . อย่างไรก็ตามปรากฏการณ์ดังกล่าวในอิทธิพลภายนอกปานกลางได้รับการปฏิบัติจริงเนื่องจากค่าสัมประสิทธิ์การลดทอนของระบบชีวภาพค่อนข้างใหญ่ อย่างไรก็ตามปรากฏการณ์เรโซแนนต์ภายใต้การกระทำของการแกว่งเชิงกลภายนอกเกิดขึ้นในอวัยวะภายใน ในเรื่องนี้เห็นได้ชัดว่าหนึ่งในสาเหตุของผลกระทบเชิงลบของความผันผวนของ Infrasound และการสั่นสะเทือนในร่างกายมนุษย์

1.7.7 Autocalbania

นอกจากนี้ยังมีระบบการสั่นสะเทือนเช่นนี้ที่ควบคุมการเติมพลังงานอสังหาริมทรัพย์เป็นระยะและจึงสามารถผันผวนเป็นเวลานาน

ความผันผวนของความผันผวนที่ไม่มีอยู่ในระบบใด ๆ ในกรณีที่ไม่มีอิทธิพลภายนอกสลับ การแกว่งตนเองและระบบเอง - ตัวสั่นตนเอง

แอมพลิจูดและความถี่ของการแกว่งตนเองขึ้นอยู่กับคุณสมบัติในระบบ Autocalibular ส่วนใหญ่ในทางตรงกันข้ามกับการบังคับของการบังคับพวกเขาจะไม่ได้รับการพิจารณาจากอิทธิพลภายนอก

ในหลาย ๆ กรณีระบบการแกว่งตนเองสามารถแสดงได้ด้วยองค์ประกอบหลักสามประการ (รูปที่ 1.7.8): 1) ระบบสั่นไหวที่เกิดขึ้นจริง 2) แหล่งพลังงาน; 3) ควบคุมการไหลของพลังงานในระบบสั่นของตัวเอง ระบบ oscillatory ช่องทาง ข้อเสนอแนะ (รูปที่ 6) ส่งผลกระทบต่อผู้ควบคุมแจ้งให้ทราบถึงหน่วยงานกำกับดูแลเกี่ยวกับสถานะของระบบนี้

ตัวอย่างคลาสสิกของระบบออโต้ออฟอัตโนมัติเชิงกลคือนาฬิกาที่ลูกตุ้มหรือความสมดุลเป็นระบบออสซิลเลสสปริงหรือเกี๊ยวที่เพิ่มขึ้น - แหล่งพลังงานและสมอเป็นตัวควบคุมการไหลของพลังงานจากแหล่งที่มาสู่แหล่งกำเนิด ระบบ.

ระบบชีวภาพจำนวนมาก (หัวใจปอด ฯลฯ ) เป็นตัวสั่นด้วยตนเอง ตัวอย่างลักษณะของระบบการสั่นอัตโนมัติแบบแม่เหล็กไฟฟ้าคือเครื่องกำเนิดไฟฟ้าของการแกว่งตนเอง

1.7.8 การเพิ่มการแกว่งของทิศทางเดียว

พิจารณาการเพิ่มการแกว่งของฮาร์มอนิกสองทิศทางเดียวกันและความถี่เดียวกัน:

x 1 \u003d a 1 cos (ω 0 T + α 1), x 2 \u003d a 2 cos (ω 0 t + α 2)

การแกว่งความกลมกลืนสามารถตั้งค่าโดยใช้เวกเตอร์ที่มีความยาวเท่ากับแอมพลิจูดของการแกว่งและทิศทางที่เกิดมุมกับแกนบางส่วนเท่ากับเฟสเริ่มต้นของการแกว่ง หากเวกเตอร์นี้หมุนด้วยความเร็วเชิงมุมω 0 การฉายภาพบนแกนที่เลือกจะเปลี่ยนไปตามกฎหมายฮาร์มอนิก จากนี้เราเลือกแกน X และจินตนาการถึงการแกว่งโดยใช้เวกเตอร์ 1 และ 2 (รูปที่ 1.7.9)

จากรูปที่ 1.7.6 มันเป็นไปตามนั้น

.

Schemes ที่การแกว่งเป็นภาพกราฟิกในรูปแบบของเวกเตอร์บนเครื่องบินเรียกว่าไดอะแกรมเวกเตอร์

จากสูตร 1.7.40 ดังนี้ เกิดอะไรขึ้นถ้าความแตกต่างของเฟสเป็นทั้งการแกว่งเท่ากับศูนย์แอมพลิจูดของการแกว่งที่เกิดขึ้นเท่ากับผลรวมของแอมพลิจูดของการแกว่งแบบพับเก็บได้ หากความแตกต่างในขั้นตอนของการแกว่งแบบพับเก็บได้เท่ากับจากนั้นแอมพลิจูดของการแกว่งที่เกิดขึ้นเท่ากับ หากความถี่ของการแกว่งที่คำนวณได้ไม่เหมือนกันเวกเตอร์ที่สอดคล้องกับความผันผวนเหล่านี้จะหมุนด้วย ความเร็วที่แตกต่างกัน. ในกรณีนี้เวกเตอร์ที่เกิดขึ้นเป็นจังหวะในขนาดและหมุนด้วยความเร็วที่ไม่ถาวร ดังนั้นอันเป็นผลมาจากการเพิ่มมันจะปรากฎว่าไม่ใช่การสั่นฮาร์มอนิก แต่กระบวนการสั่นที่ซับซ้อน

1.7.9 ไบเวีย

พิจารณาการเพิ่มการแกว่งสองแนวฮาร์มอนิกในทิศทางเดียวกันที่แตกต่างกันในความถี่ ให้ความถี่ของหนึ่งในนั้นเท่ากับωและที่สองω + δωและδω<<ω. Положим, что амплитуды складываемых колебаний одинаковы и начальные фазы обоих колебаний равны нулю. Тогда уравнения колебаний запишутся следующим образом:

x 1 \u003d a cos ωt, x 2 \u003d a cos (ω + δω) t

หลังจากสร้างนิพจน์เหล่านี้และใช้สูตรสำหรับปริมาณโคไซน์เราได้รับ:

การแกว่ง (1.7.41) ถือได้ว่าเป็นการแกว่งความเป็นแก่นแท้ของความถี่ω, แอมพลิจูดที่มีการเปลี่ยนแปลงตามกฎหมาย ฟังก์ชั่นนี้เป็นระยะด้วยความถี่ที่สูงกว่าความถี่ของนิพจน์สองเท่าภายใต้สัญลักษณ์ของโมดูล I.e. ด้วยความถี่δω ดังนั้นความถี่ของการเต้นของแอมพลิจูดเรียกว่าความถี่ของการเต้นเท่ากับความแตกต่างของความถี่ของการแกว่งแบบพับเก็บได้

1.7.10 นอกจากนี้การแกว่งแบบตั้งฉากร่วมกัน (ตัวเลข Lissuzh)

หากจุดวัสดุดำเนินการแกว่งทั้งสองตามแกน X และตามแนวแกนของ Y มันจะเคลื่อนที่ไปตามวิถี curvilinear บางอย่าง ปล่อยให้ความถี่ของการแกว่งของเดียวกันและขั้นตอนแรกของการแกว่งครั้งแรกเท่ากับศูนย์ดังนั้นสมการการแกว่งจะเขียนในแบบฟอร์ม:

สมการ (1.7.43) เป็นสมการวงรี, แกนที่มุ่งเน้นโดยพลการโดยพลการกับแกนพิกัด x และ y การวางแนวของวงรีและขนาดของแกนกึ่งขึ้นอยู่กับแอมพลิจูด A และ B และความแตกต่างของเฟสα พิจารณาบางกรณีบางกรณี:

นี่คือสมการวงรีแกนซึ่งตรงกับแกนของพิกัดและแกนกึ่งเท่ากับแอมพลิจูด (รูปที่ 1.7.12) หากแอมพลิจูดเท่ากับวงรีกลายเป็นวงกลม

รูปที่ 1.7.12

หากความถี่ของการแกว่งแบบตั้งฉากกันแตกต่างกันไปในมูลค่าต่ำδωพวกเขาถือได้ว่าเป็นการแกว่งของความถี่เดียวกัน แต่ด้วยความแตกต่างของเฟสที่เปลี่ยนแปลงอย่างช้าๆ ในกรณีนี้สมการการแกว่งสามารถบันทึกได้

x \u003d a cos ωt, y \u003d b cos [ωt + (δωt + α)]

และการแสดงออกδωt + αถือเป็นความแตกต่างของเฟสการเปลี่ยนแปลงอย่างช้า ๆ เมื่อเวลาผ่านไปตามกฎหมายเชิงเส้น การเคลื่อนไหวที่เกิดขึ้นในกรณีนี้เกิดขึ้นตามเส้นโค้งที่เปลี่ยนแปลงอย่างช้าๆซึ่งจะใช้รูปแบบที่ตรงกับค่าทั้งหมดของความแตกต่างของเฟสจาก-πถึง + π

หากความถี่ของการแกว่งตั้งฉากกันไม่เหมือนกันวิถีการเคลื่อนไหวที่เกิดขึ้นมีลักษณะของเส้นโค้งที่ซับซ้อนค่อนข้างเรียกว่า ตัวเลข lissen. ยกตัวอย่างเช่นความถี่ของการสืบค้นที่พับเป็นเป็น 1 : ความแตกต่าง 2 และเฟสπ / 2 จากนั้นสมการการแกว่งคือ

x \u003d a cos ωt, y \u003d b cos

ในช่วงเวลาเดียวกันในขณะที่แกน X จุดย้ายจากตำแหน่งที่รุนแรงไปยังอีกตำแหน่งหนึ่งไปตามแกน Y ออกมาจากตำแหน่งศูนย์มันมีเวลาที่จะบรรลุตำแหน่งที่รุนแรงหนึ่งตำแหน่งจากนั้นอีกหนึ่งและกลับมาอีกครั้ง มุมมองของเส้นโค้งแสดงในรูปที่ 1.7.13 เส้นโค้งที่มีอัตราส่วนความถี่เดียวกัน แต่ความแตกต่างของเฟสเป็นศูนย์แสดงในรูปที่ 1.7.14 อัตราส่วนของความถี่ของการแกว่งที่คำนวณได้คืนอัตราส่วนของจำนวนจุดของจุดตัดของตัวเลขที่มองไม่เห็นด้วยแกนตรงขนานของพิกัด ดังนั้นตามรูปแบบของตัวเลข Lissuzh คุณสามารถกำหนดอัตราส่วนของความถี่ของการแกว่งแบบพับเก็บได้หรือความถี่ที่ไม่รู้จัก หากหนึ่งในความถี่เป็นที่รู้จักกัน

รูปที่ 1.7.13

รูปที่ 1.7.14

การใกล้ชิดกับหน่วยที่มีเหตุผลที่แสดงความถี่ความถี่ของการแกว่งความเป็นแก่นเท่าใดตัวเลขที่ยากขึ้น

1.7.11 การกระจายคลื่นในสภาพแวดล้อมที่ยืดหยุ่น

หากในที่ใด ๆ ที่มีความยืดหยุ่น (ของเหลวของเหลวหรือก๊าซ) เพื่อเริ่มต้นการแกว่งของอนุภาคจากนั้นเนื่องจากการมีปฏิสัมพันธ์ระหว่างอนุภาคการแกว่งนี้จะถูกกระจายในสภาพแวดล้อมจากอนุภาคไปยังอนุภาคที่ความเร็วบางอย่าง กระบวนการกระจายการแกว่งในอวกาศเรียกว่า คลื่น.

อนุภาคขนาดกลางที่ใช้คลื่นไม่ได้มีส่วนร่วมในคลื่นในขบวนการแปลพวกเขาทำให้การแกว่งใกล้กับบทบัญญัติความสมดุลของพวกเขาเท่านั้น

ขึ้นอยู่กับพื้นที่ของการแกว่งของอนุภาคที่สัมพันธ์กับทิศทางที่มีการกระจายคลื่นโดดเด่น longitudinal I. ตามขวาง คลื่น. ในคลื่นยูระยะยาวปานกลางอนุภาคมีความผันผวนตามการแพร่กระจายของคลื่น ในคลื่นขวางอนุภาคปานกลางมีความผันผวนในทิศทางตั้งฉากกับทิศทางของการแพร่กระจายของคลื่น คลื่นขวางยืดหยุ่นอาจเกิดขึ้นเฉพาะในสื่อที่มีความต้านทานแรงเฉือน ดังนั้นในสื่อที่เป็นของเหลวและก๊าซเป็นไปได้ที่จะเกิดขึ้นโดยคลื่นยาวเท่านั้น ในสื่อที่เป็นของแข็งทั้งคลื่นตามยาวและตามขวางอาจเกิดขึ้นได้

ในรูปที่ 1.7.12 แสดงการเคลื่อนไหวของอนุภาคเมื่อกระจายในสื่อคลื่นขวาง ห้องพักคือ 1.2 ฯลฯ อนุภาคที่ล้าหลังซึ่งกันและกันสำหรับระยะทางเท่ากับ (¼t), I. ในระยะไกลเดินทางด้วยคลื่นสำหรับหนึ่งในสี่ของช่วงเวลาของการแกว่งที่ดำเนินการโดยอนุภาค ในเวลานั้นเวลาที่นำไปสู่ศูนย์คลื่นกระจายไปตามแกนจากซ้ายไปขวาถึงอนุภาค 1 อันเป็นผลมาจากอนุภาคเริ่มเปลี่ยนจากตำแหน่งของสมดุลขึ้นไปที่น่าสนใจอนุภาคต่อไปนี้ หนึ่งในสี่ของระยะเวลาของอนุภาค 1 ถึงตำแหน่งตอนบนสุดของความสมดุลของอนุภาค 2. เมื่อถึงไตรมาสอื่นของช่วงเวลาแรกส่วนแรกจะเป็นตำแหน่งของสมดุลเคลื่อนที่ไปในทิศทางจากบนลงล่าง อนุภาคที่สองจะถึงตำแหน่งบนสุดขั้วและอนุภาคที่สามจะเริ่มขยับตำแหน่งสมดุล ในช่วงเวลาเท่ากับ t อนุภาคแรกจะเสร็จสิ้นรอบเต็มของการแกว่งและจะอยู่ในสถานะเดียวกันของการเคลื่อนไหวเป็นคำชี้แจง คลื่นเมื่อถึงเวลาที่ผ่านไปตามเส้นทาง (υ) จะไปถึงอนุภาค 5

ในรูปที่ 1.7.13 แสดงการเคลื่อนไหวของอนุภาคเมื่อมีการกระจายคลื่นยาวในสื่อ การให้เหตุผลทั้งหมดเกี่ยวกับพฤติกรรมของอนุภาคในคลื่นขวางยังสามารถนำมาประกอบกับกรณีนี้ด้วยการแทนที่การกระจัดขึ้นและลงโดยออฟเซ็ตไปทางขวาและซ้าย

จากตัวเลขที่ชัดเจนว่าเมื่อคลื่นยาวแพร่กระจายความเข้มข้นสลับและการปล่อยอนุภาค (ไซต์ความเข้มข้นถูกล้อมรอบในรูปเส้นประ) ย้ายไปในทิศทางของการแพร่กระจายของคลื่นที่ความเร็วυ

รูปที่. 1.7.15

รูปที่. 1.7.16

ในรูปที่ 1.7.15 และ 1.7.16 แสดงการแกว่งของอนุภาคตำแหน่งสมดุลของการนอนบนแกน x.ในความเป็นจริงไม่เพียง แต่อนุภาคที่ตั้งอยู่ตามแนวแกนนั้นผันผวน xและจำนวนทั้งสิ้นของอนุภาคสรุปได้ในบางปริมาณ การแพร่กระจายจากแหล่งที่มาของการแกว่งกระบวนการคลื่นครอบคลุมชิ้นส่วนใหม่และใหม่ทั้งหมดของพื้นที่ตำแหน่งทางเรขาคณิตของจุดที่การแกว่งถึงช่วงเวลาที่เรียกว่า ด้านหน้าของคลื่น (หรือด้านหน้าของคลื่น) ด้านหน้าของคลื่นแสดงถึงพื้นผิวที่แยกส่วนของพื้นที่มีส่วนร่วมในกระบวนการคลื่นจากพื้นที่ที่การแกว่งยังไม่ได้เกิดขึ้น

ตำแหน่งทางเรขาคณิตของจุดที่มีความผันผวนในเฟสเดียวกันเรียกว่า พื้นผิวคลื่น . พื้นผิวคลื่นสามารถดำเนินการผ่านจุดใด ๆ ของพื้นที่ที่ครอบคลุมโดยกระบวนการคลื่น ดังนั้นพื้นผิวคลื่นจึงมีชุดอนันต์ในขณะที่คลื่นด้านหน้าทุกครั้งเป็นเพียงหนึ่งเดียว พื้นผิวคลื่นยังคงไม่สามารถเคลื่อนย้ายได้ (พวกเขาผ่านตำแหน่งของความสมดุลของอนุภาคความผันผวนในหนึ่งเฟส ). wavefront เคลื่อนไหวตลอดเวลา

พื้นผิวคลื่นสามารถเป็นรูปแบบใด ๆ ในกรณีที่ง่ายที่สุดพวกเขามีรูปแบบของเครื่องบินหรือทรงกลม ดังนั้นคลื่นในกรณีเหล่านี้จึงเรียกว่าแบนหรือทรงกลม ในคลื่นแบนพื้นผิวคลื่นเป็นชุดขนานกับเครื่องบินแต่ละลำในคลื่นทรงกลม - ส่วนใหญ่ของทรงกลมศูนย์กลาง

รูปที่. 1.7.17

ปล่อยให้คลื่นแบนกระจายไปตามแกน เอ็กซ์. จากนั้นจุดทั้งหมดของทรงกลมตำแหน่งสมดุลของที่มีพิกัดเดียวกัน เอ็กซ์(แต่ความแตกต่างของค่าพิกัด y.และ z)ผันผวนในระยะเดียวกัน

ในรูปที่ 1.7.17 แสดงให้เห็นถึงเส้นโค้งที่ให้การชดเชย ξ จากตำแหน่งของจุดดุลยภาพที่แตกต่างกัน เอ็กซ์ในบางจุดในเวลา คุณไม่ควรรับรู้รูปแบบนี้เป็นภาพที่มองเห็นได้ของคลื่น รูปแสดงกำหนดการของฟังก์ชั่น ξ (x, t)สำหรับบางอย่างคงที่ ช่วงเวลา t.ตารางนี้สามารถสร้างได้ทั้งในระยะยาวและสำหรับคลื่นขวาง

ระยะทางคลื่นกำลังแพร่กระจายในช่วงเวลาสั้น ๆ เท่ากับช่วงเวลาของการแกว่งของอนุภาคของสื่อเรียกว่า ความยาวคลื่น. เห็นได้ชัดว่า

ความเร็วของคลื่นคือระยะเวลาของการแกว่ง Walrow ความยาวยาวเท่ากับระยะห่างระหว่างจุดที่ใกล้ที่สุดของสื่อความผันผวนด้วยความแตกต่างของเฟสเท่ากับ2π (ดูรูปที่ 1.7.14)

การแทนที่อัตราส่วน (1.7.45) T ถึง 1 / ν (ν - ความถี่ของการแกว่ง) เราได้รับ

สูตรนี้สามารถมาจากการพิจารณาต่อไปนี้ ในหนึ่งวินาทีที่มาของคลื่นจะดำเนินการνการแกว่งสร้างขึ้นในสื่อที่มี "หวี" หนึ่ง "หวี" และคลื่น "คลื่น" หนึ่งอัน ตามเวลาที่แหล่งที่มาเสร็จสมบูรณ์ν - e ความผันผวนของ "หวี" ตัวแรกจะมีเวลาผ่านเส้นทางของคุณ ดังนั้น "สันเขา" และ "VPadin" คลื่นจะต้องพบในความยาวของυ

1.7.12 สมการคลื่นแบน

สมการคลื่นเรียกว่านิพจน์ที่ให้การกระจัดของอนุภาคสั่นเป็นฟังก์ชันของพิกัดของมัน x, y, z และเวลา ต. :

ξ \u003d ξ (x, y, z; t)

(อยู่ในใจพิกัดของตำแหน่งสมดุลของอนุภาค) คุณสมบัตินี้ต้องเป็นระยะเวลาประมาณเวลา ต. และสัมพันธ์กับพิกัด x, y, z. . ระยะเวลาดังต่อไปนี้จากความจริงที่ว่าคะแนนที่แยกออกจากกันในระยะไกล λ , ผันผวนในลักษณะเดียวกัน

ค้นหารูปแบบของฟังก์ชั่น ξ ในกรณีของคลื่นแบนสมมติว่าการแกว่งนั้นกลมกลืนกัน เพื่อลดความซับซ้อนให้ส่งแกนของพิกัดเพื่อให้แกน เอ็กซ์ ใกล้เคียงกับทิศทางของการแพร่กระจายของคลื่น จากนั้นพื้นผิวคลื่นจะตั้งฉากกับแกน เอ็กซ์ และเนื่องจากจุดทั้งหมดของพื้นผิวคลื่นมีอยู่เท่ากันออฟเซ็ต ξ จะขึ้นอยู่กับเท่านั้น เอ็กซ์ และ ต.:

ξ = ξ (x, t) .

รูปที่ 1.7.18

ปล่อยให้การแกว่งของจุดนอนอยู่ในระนาบ เอ็กซ์ = 0 (รูปที่ 1.7.18) คือ

ค้นหาประเภทของการแกว่งของคะแนนในระนาบที่สอดคล้องกับค่าโดยพลการ เอ็กซ์ . เพื่อที่จะผ่านเส้นทางจากเครื่องบิน เอ็กซ์=0 ก่อนที่ระนาบนี้คลื่นจะต้องใช้เวลา ( υ - Accpair ของการแพร่กระจายของคลื่น) ดังนั้นการแกว่งของอนุภาคที่อยู่ในระนาบ เอ็กซ์ จะล่าช้าในเวลา τ จากการแกว่งของอนุภาคในระนาบ เอ็กซ์ = 0 . จะปรากฏขึ้น

ดังนั้น, สมการคลื่นแบน (ตามยาวและขวาง) การแพร่กระจายไปในทิศทางของแกน เอ็กซ์ ดังต่อไปนี้:

การแสดงออกนี้กำหนดความสัมพันธ์ระหว่าง t และสถานที่ เอ็กซ์ ซึ่งเฟสมีค่าคงที่ ค่า DX / DX ที่เกิดขึ้นให้ความเร็วที่ค่าเฟสนี้เคลื่อนที่ แสดงออกอย่างไม่พอใจ (1.7.48) เราได้รับ

สมการของคลื่นที่แพร่กระจายไปยัง Descending เอ็กซ์ :

ในบทสรุปของสูตร (1.7.53) เราสันนิษฐานว่าแอมพลิจูดของการแกว่งไม่ได้ขึ้นอยู่กับ เอ็กซ์ . สำหรับคลื่นแบนนี่เป็นที่สังเกตในกรณีที่พลังงานคลื่นไม่ถูกดูดซึมโดยสื่อ เมื่อกระจายในการดูดซับพลังงานความเข้มของคลื่นที่มีการกำจัดออกจากแหล่งกำเนิดของการสั่นจะค่อยๆลดลง - คลื่นจะลดทอน ประสบการณ์แสดงให้เห็นว่าในสื่อที่เป็นเนื้อเดียวกันการลดทอนดังกล่าวเกิดขึ้นในกฎหมายเลขชี้กำลัง:

ตามลำดับ สมการคลื่นแบนโดยคำนึงถึงการลดทอนบัญชีมันมีรูปแบบต่อไปนี้:

(0 - แอมพลิจูดที่จุดของเครื่องบิน x \u003d 0)