Open Library - an open library of educational information. Exposed windblown Pythagorean tree Using a recursive procedure to construct the figure of a Pythagorean tree

12.01.2024

Epithets in prophetic Oleg. A. S. Pushkin “Song of the prophetic Oleg”: analysis of the poem. Structural analysis of the poem

Bank reporting under IFRS - new requirements Bank reporting under IFRS

The Pythagorean tree is a type of fractal that is based on a figure known as Pythagorean Pants.

Proving his famous theorem, Pythagoras constructed a figure in which there were squares on each side of a right triangle. Over time, this figure of Pythagoras turned into a whole tree. The first to construct the Pythagorean tree during the Second World War was A. Bosman, using an ordinary drawing ruler.

One of the main properties of the Pythagorean tree is that when the area of the first square is one, then at each level the sum of the areas of the squares will also be equal to one. The classic Pythagorean tree has an angle of 45 degrees, but it is also possible to construct a generalized Pythagorean tree using other angles. Such a tree is called the wind-blown tree of Pythagoras. If you draw only the segments that somehow connect certain “centers” of the triangles, then you get a naked Pythagorean tree.

Another example would be the famous "Pythagorean tree". It is often depicted as shown in Fig. 3.2. Each of the right triangles in this tree has an interior angle of 45°.

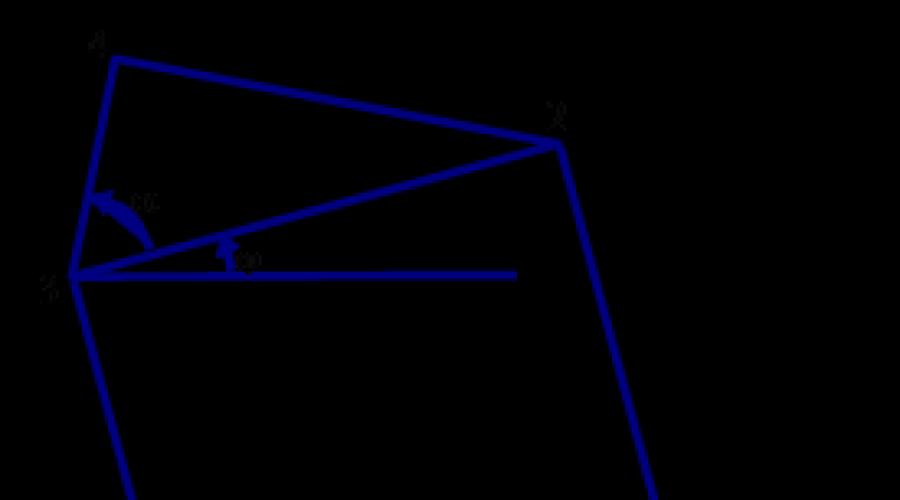
Again, we will use a random number generator to create a more general program that can generate not only rice. 3.2, but also generate less regular trees. Angles set to 45° for Fig. 3.2, in general, will be set randomly within the range between (45 - delta)° and (45 + delta)° , where is the value delta is given as an input parameter along with the parameter n, which determines the recursion depth. The regular version shown in Fig. 3.2, obtained by specifying delta= 0 and n = 7. In the figure, the parameter P determines the number of triangles on the path from the root to the leaves of the tree. The core of the program will be the recursive function square_and_triangle ("square and triangle") with the parameter n, which determines the depth of the recursion, as the first argument. If the value of the parameter n is greater than zero, then the function of square_and_triangle, as its name implies, will draw a square and a triangle over it, and then call itself twice more with the corresponding new arguments, the first of which is set to n-1. The size and position of the square are completely determined by four parameters: X0, Y0, a and j (see Fig. 3.3). To draw a triangle, you need to know the angle a. This angle, expressed in degrees, is equal to 45+deviation, where deviation is equal to one of the integers of the series -delta, -delta+I, ... , delta, chosen at random. In Fig. 3.3 the necessary points are numbered consecutive numbers 0,1,2,3,4. The coordinates X0, Y0 of point O are specified in a call to the function. To calculate the remaining points, we first consider a simpler situation with j = 0, that is, when the side 0 1 of the square occupies a horizontal position.

In this position, the coordinates of the points are very easy to determine. They are stored in the x and y arrays. Then the entire structure is rotated around point O by angle j. The result of the rotation is recorded in the xx and yy arrays.

/* PYTH_TREE: Variant of the Pythagorean tree */

#include "math.h"

#include "stdlib.h"

#include "time.h"

#define pi 3.1415927

#include "stdio.h"

struct (float xx; float yy; int ii;) s;

void pfopen())( fp=fopen("scratch", "wb"); )

void pmove(float x,float y)

( s.xx=x; s.yy=y; s.ii=0; /* 0 = pen up */ /* 0 = pen up */

fwrite(&s, sizeof s, 1, fp);

void pdraw(float x,float y)

( s.xx=x; s.yy=y; s.ii=1; /* 1 = pen down */ /* 1 = pen down */

fwrite(&s, sizeof s, 1, fp);

void pfclose())( fclose(fp); )

void square_and_triangle(int n,float x0,float y0, float a, float phi)

( float x, y, xx, yy, cphi, sphi, c1, c2, b, c,

alpha, calpha, salpha;

int i, deviation; /* phi and alpha in radians */

/* delta in degrees */

if(n==0) return; /* angles phi and alpha in radians */

/* angle delta in degrees */

deviation=rand()%(2*delta+1)-delta;

alpha=(45+deviation)*pi/180.0;

x=x=x0; x=x=x0+a;

y=y=y0; y=y=y0+a;

calpha=cos(alpha); salpha=sin(alpha);

c=a*calpha; b=a*salpha;

/* Rotation about (x0, y0) through angle phi ; */

/* Rotate around the point (x0, y0) by angle phi;*/

cphi=cos(phi); sphi=sin(phi);

c1=x0-x0*cphi+y0*sphi;

c2=y0-x0*sphi-y0*cphi;

for (i=0; i<5; i++)

( xx[i]=x[i]*cphi-y[i]*sphi+c1;

yy[i]=x[i]*sphi+y[i]*cphi+c2;

for (i=0; i<5; i++) pdraw(xx[i],yy[i]);

square_and_triangle(n-1, xx, yy, c, phi+alpha);

square_and_triangle(n-1, xx, yy, b, phi+alpha-0.5*pi);

pfopen(); time(&seed); srand((int)seed);

printf(" Set delta angle in degrees (0< delta < 45) ");

scanf("%d", &delta);

printf(" Set recursion depth n "); scanf("%d", &n);

square_and_triangle(n, 0.0, 0.0, 1.0, 0.0);

This program generates a file SCRATCH which must be processed by the G program ENPLOT from lecture 2. Graphical result of the program for delta= 30 and n = 7 is shown in Fig. 3.4.

The Pythagorean tree is a type of fractal that is based on a figure known as Pythagorean Pants.

The Mandelbrot set is a classic example of a fractal... Wikipedia

HTML HTML and HTML5 Dynamic HTML ... Wikipedia

The Mandelbrot set is a classic example of a fractal. Fractal (lat. fractus crushed) is a term meaning a geometric figure that has the property of self-similarity, that is, composed of several parts, each of which is similar to the entire figure... ... Wikipedia

Levy curve fractal. Proposed by the French mathematician P. Levy. It turns out if you take half a square of the form /, and then replace each side with the same fragment, and, repeating this operation, in ... Wikipedia

Newton Pools ... Wikipedia

Cayley graph is a graph that is constructed from a group with a distinguished system of generators. Named after Caylee. Definition Let a discrete group G and a system of generators S be given. Suppose S = S − 1, that is, for each. Cayley count of group G according to the system... ... Wikipedia

A graph that is constructed from a group with a dedicated system of generators. Named after Caylee. Definition Let a discrete group and a system of generators be given. Let's assume, that is, for each. Count Cayley group ... Wikipedia

Ancient Iranian religion in ancient sources. The article contains a review of information from ancient authors (ancient Greek, Latin and partly Armenian and Syrian) of the 5th century BC. e. 6th century AD e. about the religion of the Iranian peoples of the Achaemenid era, the Parthians and the power ... Wikipedia

The culture of the peoples who inhabited it in ancient times, in the 4th 1st millennium BC. e., Mesopotamia Mesopotamia Tigris and Euphrates (the territory of modern Iraq), Sumerians and Akkadians, Babylonians and Assyrians, who created the large states of Sumer, Akkad, Babylonia (See... ... Great Soviet Encyclopedia

Books

At the end of summer, Vera Orlovskaya. Vera Orlovskaya’s new book AT THE END OF SUMMER continues to amaze the reader with its variety of forms and what some of the titles suggest: PYTHAGORUS’ PHILOSOPHY IN NUMBERS, THE TREE OF DREAM, SYMPHONY No. 1...
R-functions as a device in applications of fractal geometry, A. V. Tolok. The mathematical apparatus of the theory of R-functions is used to describe objects of fractal geometry by the functions ɷ(x) = 0, x ∈ En, where ɷ(x) has the form of a single analytical expression. By…

Hello, friends interested in fractals and more. Starting from this moment, I am launching a series of posts in which I will explain the principles of constructing the simplest fractals. It is always interesting to study and I will help you with this: from now on we will know many, many fractals. The Lorenz attractor in the article about chaos was an example of this. And today I will tell you about the Pythagorean tree.

So what is it? The Pythagorean tree is the simplest fractal that can be drawn on paper. But why is this fractal called the Pythagorean tree? The fact is that there is a connection here with the Pythagorean theorem - one of the foundations of Euclidean geometry. Remember her? Let me remind you: a2 + b2 = c2 (the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse). This theorem has been known since ancient times; there are currently more than 400 proofs of the theorem, and only Pythagoras was the first to prove it geometrically. He built the following figure: he took a right triangle and drew squares on its sides. This figure is also called “Pythagorean pants”:

If we continue this construction recursively, we end up with a Pythagorean tree:
1st iteration (in our Pythagorean tree the angle is 45 degrees):

Second iteration:

Third iteration:

Tenth iteration:

An important property of the Pythagorean tree: if the area of the first square is equal to one, then at each level the sum of the areas of the squares will also be equal to one.
If the angle is changed from 45 degrees, then other types of Pythagorean tree can be constructed.
Here, for example, is the so-called “wind-blown tree of Pythagoras”:

Some fractal graphics generators implement a formula for constructing a fractal based on the Pythagorean tree. This implementation is very reminiscent of the IFS system, especially if you replace the squares with rectangles or elongated shapes.
That's all for today, until the next meetings, in which there will be many other interesting fractals)

Open Library - an open library of educational information. Exposed windblown Pythagorean tree Using a recursive procedure to construct the figure of a Pythagorean tree

Read also

Books