วิธีการสร้างแบบจำลองเชิงวิเคราะห์ของฟังก์ชันเชิงเส้น การศึกษาฟังก์ชันเชิงเส้น การคุ้มครองข้อมูลส่วนบุคคล
การรักษาความเป็นส่วนตัวของคุณเป็นสิ่งสำคัญสำหรับเรา ด้วยเหตุนี้ เราจึงได้พัฒนานโยบายความเป็นส่วนตัวที่อธิบายถึงวิธีที่เราใช้และจัดเก็บข้อมูลของคุณ โปรดตรวจสอบหลักปฏิบัติด้านความเป็นส่วนตัวของเราและแจ้งให้เราทราบหากคุณมีคำถามใดๆ
การรวบรวมและการใช้ข้อมูลส่วนบุคคล
ข้อมูลส่วนบุคคลหมายถึงข้อมูลที่สามารถใช้เพื่อระบุหรือติดต่อบุคคลใดบุคคลหนึ่งโดยเฉพาะ
คุณอาจถูกขอให้ให้ข้อมูลส่วนบุคคลของคุณได้ตลอดเวลาเมื่อคุณติดต่อเรา
ด้านล่างนี้คือตัวอย่างบางส่วนของประเภทของข้อมูลส่วนบุคคลที่เราอาจรวบรวมและวิธีที่เราอาจใช้ข้อมูลดังกล่าว
เราเก็บรวบรวมข้อมูลส่วนบุคคลอะไรบ้าง:
- เมื่อคุณส่งใบสมัครบนเว็บไซต์ เราอาจรวบรวมข้อมูลต่าง ๆ รวมถึงชื่อ หมายเลขโทรศัพท์ ที่อยู่อีเมลของคุณ ฯลฯ
เราใช้ข้อมูลส่วนบุคคลของคุณอย่างไร:
- ข้อมูลส่วนบุคคลที่เรารวบรวมช่วยให้เราสามารถติดต่อคุณเพื่อรับข้อเสนอ โปรโมชั่น และกิจกรรมอื่น ๆ และกิจกรรมที่กำลังจะเกิดขึ้น
- ในบางครั้ง เราอาจใช้ข้อมูลส่วนบุคคลของคุณเพื่อส่งประกาศและการสื่อสารที่สำคัญ
- เรายังอาจใช้ข้อมูลส่วนบุคคลเพื่อวัตถุประสงค์ภายใน เช่น การดำเนินการตรวจสอบ การวิเคราะห์ข้อมูล และการวิจัยต่างๆ เพื่อปรับปรุงบริการที่เรามีให้และให้คำแนะนำเกี่ยวกับบริการของเรา
- หากคุณเข้าร่วมการจับรางวัล การประกวด หรือการส่งเสริมการขายที่คล้ายกัน เราอาจใช้ข้อมูลที่คุณให้ไว้เพื่อจัดการโปรแกรมดังกล่าว
การเปิดเผยข้อมูลแก่บุคคลที่สาม
เราไม่เปิดเผยข้อมูลที่ได้รับจากคุณต่อบุคคลที่สาม
ข้อยกเว้น:
- หากจำเป็น - ตามกฎหมาย ขั้นตอนการพิจารณาคดี ในการดำเนินการทางกฎหมาย และ/หรือตามคำขอสาธารณะหรือคำขอจากหน่วยงานของรัฐในสหพันธรัฐรัสเซีย - ให้เปิดเผยข้อมูลส่วนบุคคลของคุณ เรายังอาจเปิดเผยข้อมูลเกี่ยวกับคุณหากเราพิจารณาว่าการเปิดเผยดังกล่าวมีความจำเป็นหรือเหมาะสมเพื่อความปลอดภัย การบังคับใช้กฎหมาย หรือวัตถุประสงค์ที่สำคัญสาธารณะอื่น ๆ
- ในกรณีของการปรับโครงสร้างองค์กร การควบรวมกิจการ หรือการขาย เราอาจถ่ายโอนข้อมูลส่วนบุคคลที่เรารวบรวมไปยังบุคคลที่สามที่รับช่วงต่อที่เกี่ยวข้อง
การคุ้มครองข้อมูลส่วนบุคคล
เราใช้ความระมัดระวัง - รวมถึงการบริหารจัดการ ทางเทคนิค และทางกายภาพ - เพื่อปกป้องข้อมูลส่วนบุคคลของคุณจากการสูญหาย การโจรกรรม และการใช้งานในทางที่ผิด รวมถึงการเข้าถึง การเปิดเผย การเปลี่ยนแปลง และการทำลายโดยไม่ได้รับอนุญาต
การเคารพความเป็นส่วนตัวของคุณในระดับบริษัท
เพื่อให้มั่นใจว่าข้อมูลส่วนบุคคลของคุณปลอดภัย เราจะสื่อสารมาตรฐานความเป็นส่วนตัวและความปลอดภัยให้กับพนักงานของเรา และบังคับใช้หลักปฏิบัติด้านความเป็นส่วนตัวอย่างเคร่งครัด
สรุปและจัดระบบความรู้ในหัวข้อ “ฟังก์ชันเชิงเส้น”:
- รวมความสามารถในการอ่านและสร้างกราฟของฟังก์ชันที่กำหนดโดยสูตร y = kx+b, y = kx;
- รวมความสามารถในการกำหนดตำแหน่งสัมพัทธ์ของกราฟของฟังก์ชันเชิงเส้น
- พัฒนาทักษะในการทำงานกับกราฟของฟังก์ชันเชิงเส้น
พัฒนาความสามารถในการวิเคราะห์ เปรียบเทียบ สรุปผล การพัฒนาความสนใจทางปัญญาในด้านคณิตศาสตร์ ความสามารถในการพูดทางคณิตศาสตร์ด้วยวาจา ความแม่นยำและความแม่นยำในการก่อสร้าง
การเลี้ยงดูความเอาใจใส่ ความเป็นอิสระในการทำงาน ความสามารถในการทำงานเป็นคู่
อุปกรณ์ : ไม้บรรทัด ดินสอ การ์ดงาน ดินสอสี
ประเภทบทเรียน: บทเรียนเกี่ยวกับการรวบรวมเนื้อหาที่เรียน
แผนการเรียน:
- เวลาจัดงาน.
- งานช่องปาก. การเขียนตามคำบอกทางคณิตศาสตร์พร้อมการทดสอบตนเองและการประเมินตนเอง ทัศนศึกษาทางประวัติศาสตร์
- แบบฝึกหัดการฝึกอบรม
- ทำงานอิสระ.
- สรุปบทเรียน
- การบ้าน.
ในระหว่างเรียน
1. ระบุจุดประสงค์ของบทเรียน
วัตถุประสงค์ของบทเรียนคือการสรุปและจัดระบบความรู้ในหัวข้อ “ฟังก์ชันเชิงเส้น”
2. เริ่มต้นด้วยการทดสอบความรู้ทางทฤษฎีของคุณ
– กำหนดฟังก์ชั่น ตัวแปรอิสระคืออะไร? ตัวแปรตาม?
– กำหนดกราฟของฟังก์ชัน
– กำหนดนิยามของฟังก์ชันเชิงเส้น
– กราฟของฟังก์ชันเชิงเส้นคืออะไร?
– วิธีการสร้างกราฟฟังก์ชันเชิงเส้น?
– กำหนดคำจำกัดความของสัดส่วนโดยตรง กราฟคืออะไร? จะสร้างกราฟได้อย่างไร? กราฟของฟังก์ชัน y = kx อยู่ในระนาบพิกัดสำหรับ k > 0 และสำหรับ k อย่างไร< 0?
การเขียนตามคำบอกทางคณิตศาสตร์พร้อมการทดสอบตนเองและการประเมินตนเอง
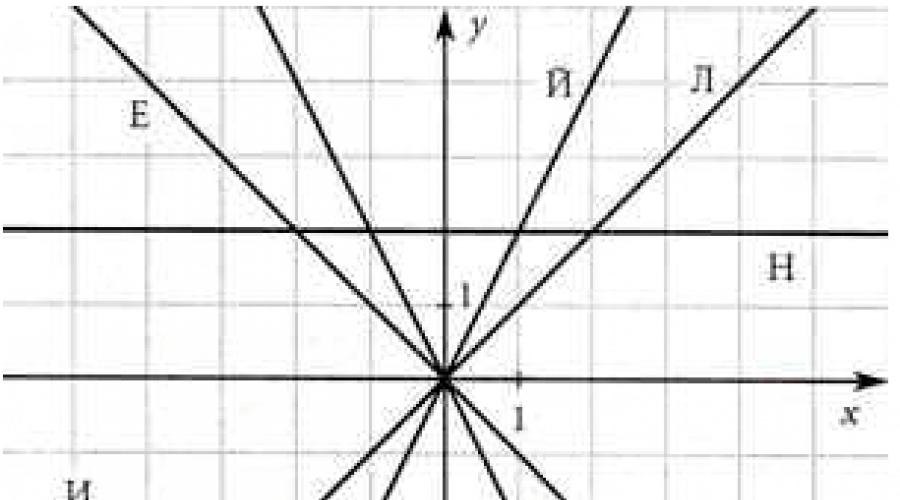
ดูภาพแล้วตอบคำถาม
1) กราฟของฟังก์ชันใดซ้ำซ้อน
2) รูปใดแสดงกราฟสัดส่วนตรง
3) กราฟของฟังก์ชันเชิงเส้นมีความชันเป็นลบในรูปใด
4) กำหนดเครื่องหมายของหมายเลข b (เขียนคำตอบเป็นอสมการ)
ตรวจสอบงาน. เรตติ้ง.
ทำงานเป็นคู่.
ถอดรหัสชื่อของนักคณิตศาสตร์ที่ใช้คำว่าฟังก์ชันเป็นคนแรก เมื่อต้องการทำสิ่งนี้ ให้เขียนตัวอักษรลงในกล่องที่ตรงกับกราฟของฟังก์ชันที่กำหนด เขียนตัวอักษร C ในช่องสี่เหลี่ยมที่เหลือ วาดรูปด้วยกราฟของฟังก์ชันที่ตรงกับตัวอักษรนี้

ภาพที่ 1

รูปที่ 2

รูปที่ 3
กอตต์ฟรีด วิลเฮล์ม ไลบ์นิซ (ค.ศ. 1646-1716) นักปรัชญา นักคณิตศาสตร์ นักฟิสิกส์ และนักภาษาศาสตร์ชาวเยอรมัน เขาและนักวิทยาศาสตร์ชาวอังกฤษ I. Newton ได้สร้างรากฐานของสาขาวิชาคณิตศาสตร์ที่สำคัญ - การวิเคราะห์ทางคณิตศาสตร์ (โดยแยกจากกัน) ไลบ์นิซแนะนำแนวคิดและสัญลักษณ์มากมายที่ยังคงใช้ในคณิตศาสตร์จนถึงทุกวันนี้
3. 1. รับฟังก์ชันที่ระบุโดยสูตร: y = x-5; y = 0.5x; ย = – 2x; ย = 4.
ตั้งชื่อฟังก์ชัน ระบุว่ากราฟใดของฟังก์ชันเหล่านี้จะผ่านจุด M (8;4) แสดงแผนผังว่าภาพวาดจะมีลักษณะอย่างไรหากคุณพรรณนากราฟของฟังก์ชันที่ผ่านจุด M บนภาพวาดนั้น

2. กราฟของสัดส่วนโดยตรงผ่านจุด C (2;1) สร้างสูตรที่ระบุสัดส่วนโดยตรง กราฟจะผ่านจุด B (-4;m) ที่มีค่า m เท่าใด
3. สร้างกราฟฟังก์ชันที่กำหนดโดย y=1/2X คุณจะหากราฟของฟังก์ชันที่กำหนดโดยสูตร y=1/2X – 4 และ y = 1/2X+3 จากกราฟของฟังก์ชันที่กำหนดได้อย่างไร วิเคราะห์กราฟผลลัพธ์
4. ฟังก์ชันถูกกำหนดโดยสูตร:
1) y= 4x+9 และ y= 6x-5;
2) y=1/2x-3 และ y=0.5x+2;
3) y= x และ y= -5x+2.4;
4) y= 3x+6 และ y= -2.5x+6
ตำแหน่งสัมพันธ์ของกราฟฟังก์ชันคืออะไร? โดยไม่ต้องทำการก่อสร้าง ให้ค้นหาพิกัดของจุดตัดของกราฟคู่แรก (ทดสอบตัวเอง)
4. งานอิสระเป็นคู่ (แสดงบนกระดาษมล.) การสื่อสารระหว่างวิชา
มีความจำเป็นต้องสร้างกราฟของฟังก์ชันและเลือกส่วนนั้นสำหรับจุดที่มีความไม่เท่าเทียมกันที่สอดคล้องกัน:
y = x + 6, 4 < เอ็กซ์ < 6; y = -x + 6, -6 < เอ็กซ์ < -4; y = – 1/3 x + 10, -6 < เอ็กซ์ < -3; y = 1/3 x +10, 3 < เอ็กซ์ < 6; y = -x + 14, 0 < เอ็กซ์ < 3; y = x + 14, -3 < เอ็กซ์ < 0; y = 9x – 18, 2 < เอ็กซ์ < 4; ย = – 9x – 18 -4 < เอ็กซ์ < -2; ย = 0, -2 < เอ็กซ์ < 2.
คุณได้รับการวาดภาพประเภทใด? - ทิวลิป.)

เล็กน้อยเกี่ยวกับดอกทิวลิป:
ทิวลิปเป็นที่รู้จักประมาณ 120 สายพันธุ์ โดยส่วนใหญ่กระจายอยู่ในเอเชียกลาง เอเชียตะวันออก เอเชียใต้ และยุโรปใต้ นักพฤกษศาสตร์เชื่อว่าวัฒนธรรมทิวลิปมีต้นกำเนิดในตุรกีในศตวรรษที่ 12 พืชดังกล่าวได้รับชื่อเสียงไปทั่วโลกซึ่งห่างไกลจากบ้านเกิดในฮอลแลนด์ ซึ่งเรียกอย่างถูกต้องว่าดินแดนแห่งทิวลิป
นี่คือตำนานเกี่ยวกับดอกทิวลิป ความสุขอยู่ในดอกตูมสีทองของดอกทิวลิปสีเหลือง ไม่มีใครสามารถเข้าถึงความสุขนี้ได้ เพราะไม่มีพลังใดที่จะเปิดตาของมันได้ แต่วันหนึ่งมีผู้หญิงกับลูกคนหนึ่งกำลังเดินผ่านทุ่งหญ้า เด็กชายหนีจากอ้อมแขนของแม่ วิ่งขึ้นไปบนดอกไม้พร้อมกับหัวเราะกึกก้อง และดอกตูมสีทองก็เปิดออก เสียงหัวเราะที่ไร้ความกังวลของเด็กๆ บรรลุผลสำเร็จในสิ่งที่ไม่มีกำลังจะทำได้ ตั้งแต่นั้นมา ได้กลายเป็นธรรมเนียมที่จะมอบดอกทิวลิปให้กับผู้ที่มีความสุขเท่านั้น
การบ้านที่สร้างสรรค์ สร้างภาพวาดในระบบพิกัดสี่เหลี่ยม ประกอบด้วยส่วนต่างๆ และสร้างแบบจำลองการวิเคราะห์ของระบบ
6. งานอิสระ งานที่แตกต่าง (ในสองเวอร์ชัน)
ตัวเลือกที่ 1:
ร่างกราฟของฟังก์ชัน:

ตัวเลือกที่สอง:
วาดกราฟของฟังก์ชันตามแผนผังซึ่งตรงตามเงื่อนไขต่อไปนี้:

7. สรุปบทเรียน
การวิเคราะห์งานที่ทำ การให้เกรด
คำแนะนำ
หากต้องการค้นหาพิกัดของจุดบนเส้น ให้เลือกจุดบนเส้นแล้ววาดเส้นตั้งฉากบนแกนพิกัด กำหนดว่าจุดตัดตรงกับจำนวนใด จุดตัดกับแกน x คือค่า Abscissa นั่นคือ x1 จุดตัดกับแกน y คือพิกัด y1
ลองเลือกจุดที่สามารถกำหนดพิกัดได้โดยไม่มีค่าเศษส่วน เพื่อความสะดวกและแม่นยำในการคำนวณ ในการสร้างสมการ คุณต้องมีจุดอย่างน้อยสองจุด ค้นหาพิกัดของจุดอื่นที่เป็นของเส้นนี้ (x2, y2)
แทนค่าพิกัดลงในสมการของเส้นตรงที่มีรูปแบบทั่วไป y=kx+b คุณจะได้ระบบสองสมการ y1=kx1+b และ y2=kx2+b แก้ระบบนี้ ดังตัวอย่างต่อไปนี้
เขียน b จากสมการแรกแล้วแทนค่าลงในสมการที่สอง หา k แทนลงในสมการใดๆ แล้วหา b ตัวอย่างเช่น คำตอบของระบบ 1=2k+b และ 3=5k+b จะมีลักษณะดังนี้: b=1-2k, 3=5k+(1-2k); 3k=2, k=1.5, b=1-2*1.5=-2 ดังนั้นสมการของเส้นตรงคือ y=1.5x-2
เมื่อทราบจุดสองจุดที่เป็นของเส้นตรงแล้ว ให้ลองใช้สมการมาตรฐานของเส้นตรง ซึ่งจะมีลักษณะดังนี้: (x - x1)/(x2 - x1) = (y - y1)/(y2 - y1) แทนค่า (x1;y1) และ (x2;y2) ทำให้ง่ายขึ้น ตัวอย่างเช่น จุด (2;3) และ (-1;5) อยู่ในเส้นตรง (x-2)/(-1-2)=(y-3)/(5-3); -3(x-2)=2(y-3); -3x+6=2y-6; 2y=12-3x หรือ y=6-1.5x
หากต้องการค้นหาสมการของฟังก์ชันที่มีกราฟไม่เชิงเส้น ให้ดำเนินการดังนี้ ดูแผนภูมิมาตรฐานทั้งหมด y=x^2, y=x^3, y=√x, y=sinx, y=cosx, y=tgx ฯลฯ หากหนึ่งในนั้นทำให้คุณนึกถึงตารางเวลาของคุณ ให้ใช้เป็นพื้นฐาน
วาดกราฟมาตรฐานของฟังก์ชันฐานบนแกนพิกัดเดียวกันแล้วค้นหาจากกราฟของคุณ หากกราฟถูกย้ายขึ้นหรือลงหลายหน่วย แสดงว่าตัวเลขนี้ได้ถูกเพิ่มเข้าไปในฟังก์ชันแล้ว (เช่น y=sinx+4) ถ้ากราฟถูกย้ายไปทางขวาหรือซ้าย หมายความว่ามีการเพิ่มตัวเลขลงในอาร์กิวเมนต์แล้ว (เช่น y=sin (x+P/2)
กราฟความสูงที่มีความยาวแสดงว่าฟังก์ชันอาร์กิวเมนต์ถูกคูณด้วยตัวเลขจำนวนหนึ่ง (เช่น y=2sinx) ในทางกลับกัน หากกราฟมีความสูงลดลง แสดงว่าตัวเลขที่อยู่หน้าฟังก์ชันมีค่าน้อยกว่า 1
เปรียบเทียบกราฟของฟังก์ชันฐานกับฟังก์ชันของคุณตามความกว้าง หากแคบกว่า x จะนำหน้าด้วยตัวเลขที่มากกว่า 1 กว้าง - ตัวเลขที่น้อยกว่า 1 (เช่น y=sin0.5x)
บันทึก
บางทีกราฟอาจสอดคล้องกับสมการที่พบเฉพาะในส่วนใดส่วนหนึ่งเท่านั้น ในกรณีนี้ให้ระบุว่าค่า x ของความเท่าเทียมกันที่เกิดขึ้นมีค่าเท่าใด
เส้นตรงคือเส้นพีชคณิตของลำดับแรก ในระบบพิกัดคาร์ทีเซียนบนเครื่องบิน สมการของเส้นตรงจะได้รับจากสมการระดับแรก
คุณจะต้องการ
- ความรู้เกี่ยวกับเรขาคณิตวิเคราะห์ ความรู้พื้นฐานเกี่ยวกับพีชคณิต
คำแนะนำ
สมการนี้ถูกกำหนดโดยสองซึ่งเส้นตรงนี้จะต้องผ่าน มาสร้างอัตราส่วนของพิกัดของจุดเหล่านี้กัน ให้จุดแรกมีพิกัด (x1,y1) และจุดที่สอง (x2,y2) จากนั้นสมการของเส้นตรงจะเขียนได้ดังนี้: (x-x1)/(x2-x1) = (y-y1 )(y2-y1)
ลองแปลงสมการเส้นตรงที่ได้แล้วเขียน y ให้ชัดเจนในรูปของ x หลังจากการดำเนินการนี้ สมการของเส้นตรงจะอยู่ในรูปแบบสุดท้าย: y=(x-x1)/((x2-x1)*(y2-y1))+y1
วิดีโอในหัวข้อ
บันทึก
ถ้าตัวเลขตัวใดตัวหนึ่งในตัวส่วนเป็นศูนย์ แสดงว่าเส้นขนานนั้นขนานกับแกนพิกัดแกนใดแกนหนึ่ง
คำแนะนำที่เป็นประโยชน์
หลังจากที่คุณเขียนสมการของเส้นแล้ว ให้ตรวจสอบความถูกต้อง เมื่อต้องการทำเช่นนี้ ให้แทนที่พิกัดของจุดแทนพิกัดที่เกี่ยวข้อง และตรวจสอบให้แน่ใจว่ามีความเท่าเทียมกัน
เป็นที่ทราบกันดีว่า y ขึ้นอยู่กับ x เป็นเส้นตรง และให้กราฟของการพึ่งพานี้มา ในกรณีนี้ สามารถหาสมการของเส้นตรงได้ ก่อนอื่นคุณต้องเลือกสองจุดบนเส้นตรง

คำแนะนำ
ค้นหาจุดที่เลือก เมื่อต้องการทำสิ่งนี้ ให้ลดตั้งฉากลงจากจุดบนแกนพิกัดแล้วจดตัวเลขจากสเกล ดังนั้นสำหรับจุด B จากตัวอย่างของเรา พิกัด x คือ -2 และพิกัด y คือ 0 ในทำนองเดียวกัน สำหรับจุด A พิกัดจะเป็น (2;3)
เป็นที่ทราบกันว่าเส้นตรงมีรูปแบบ y = kx + b เราแทนที่พิกัดของจุดที่เลือกลงในสมการในรูปแบบทั่วไป จากนั้นสำหรับจุด A เราจะได้สมการต่อไปนี้: 3 = 2k + b สำหรับจุด B เราจะได้สมการอื่น: 0 = -2k + b แน่นอนว่า เรามีระบบสมการสองสมการที่ไม่ทราบค่าสองตัว: k และ b
จากนั้นเราจะแก้ไขระบบด้วยวิธีที่สะดวก ในกรณีของเรา คุณสามารถเพิ่มสมการของระบบได้ เนื่องจาก k ที่ไม่ทราบค่ารวมอยู่ในสมการทั้งสองที่มีค่าสัมประสิทธิ์ซึ่งมีขนาดเท่ากันแต่มีเครื่องหมายตรงกันข้าม จากนั้นเราจะได้ 3 + 0 = 2k - 2k + b + b หรือเท่ากัน: 3 = 2b ดังนั้น b = 3/2 แทนค่าที่พบของ b ลงในสมการใดๆ เพื่อหา k จากนั้น 0 = -2k + 3/2, k = 3/4
ลองแทนค่า k และ b ที่พบลงในสมการทั่วไปแล้วได้สมการเส้นตรงที่ต้องการ: y = 3x/4 + 3/2
วิดีโอในหัวข้อ
บันทึก
ค่าสัมประสิทธิ์ k เรียกว่าความชันของเส้นตรงและเท่ากับค่าแทนเจนต์ของมุมระหว่างเส้นตรงกับแกน x
เส้นตรงสามารถลากได้จากสองจุด พิกัดของจุดเหล่านี้ "ซ่อน" ไว้ในสมการของเส้นตรง สมการจะบอกความลับทั้งหมดเกี่ยวกับเส้นนี้ให้คุณทราบ เช่น หมุนอย่างไร อยู่ด้านใดของระนาบพิกัด เป็นต้น

คำแนะนำ
บ่อยครั้งจำเป็นต้องสร้างบนเครื่องบิน แต่ละจุดจะมีพิกัดสองจุด: x, y ให้ความสนใจกับสมการ โดยเป็นไปตามรูปแบบทั่วไป: y=k*x ±b โดยที่ k, b เป็นตัวเลขอิสระ และ y, x เป็นพิกัดเดียวกันของทุกจุดบนเส้นตรงจากสมการทั่วไป นั่นคือถึง ค้นหาพิกัด y ที่คุณต้องรู้พิกัด x สิ่งที่น่าสนใจที่สุดคือคุณสามารถเลือกค่าใดก็ได้สำหรับพิกัด x: จากค่าอนันต์ทั้งหมดของตัวเลขที่รู้จัก ต่อไป แทน x ลงในสมการแล้วแก้โจทย์เพื่อหา y ตัวอย่าง. ให้สมการได้รับ: y=4x-3 คิดค่าสองค่าใดก็ได้สำหรับพิกัดของจุดสองจุด ตัวอย่างเช่น x1 = 1, x2 = 5 แทนค่าเหล่านี้ลงในสมการเพื่อค้นหาพิกัด y y1 = 4*1 – 3 = 1 y2 = 4*5 – 3 = 17 เราได้สองจุด A และ B, A (1; 1) และ B (5; 17)
คุณควรพล็อตจุดที่พบในแกนพิกัด เชื่อมต่อกันและดูเส้นตรงที่สมการอธิบายไว้ ในการสร้างเส้นตรง คุณต้องทำงานในระบบพิกัดคาร์ทีเซียน วาดแกน X และ Y ตั้งค่าเป็น "ศูนย์" ที่จุดตัดกัน พล็อตตัวเลขบนแกน
ในระบบที่สร้างขึ้น ให้ทำเครื่องหมายสองจุดที่พบในขั้นตอนที่ 1 หลักการตั้งค่าจุดที่ระบุ: จุด A มีพิกัด x1 = 1, y1 = 1; บนแกน X เลือกหมายเลข 1 บนแกน Y – หมายเลข 1 จุด A อยู่ที่จุดนี้ จุด B กำหนดโดยค่า x2 = 5, y2 = 17 โดยการเปรียบเทียบให้ค้นหาจุด B บนกราฟ เชื่อมต่อ A และ B เพื่อสร้างเส้นตรง
วิดีโอในหัวข้อ
คำว่าแก้ฟังก์ชันเช่นนี้ไม่ได้ใช้ในวิชาคณิตศาสตร์ ควรเข้าใจว่าสูตรนี้ดำเนินการบางอย่างกับฟังก์ชันที่กำหนดเพื่อค้นหาคุณลักษณะเฉพาะ ตลอดจนค้นหาข้อมูลที่จำเป็นสำหรับการสร้างกราฟของฟังก์ชัน

คำแนะนำ
คุณสามารถพิจารณาแผนภาพโดยประมาณตามพฤติกรรมของฟังก์ชันที่เหมาะสมและสร้างกราฟได้
ค้นหาโดเมนของฟังก์ชัน ตรวจสอบว่าฟังก์ชันเป็นเลขคู่หรือคี่ หากคุณพบคำตอบที่ต้องการ ให้ดำเนินการต่อเฉพาะครึ่งแกนที่ต้องการเท่านั้น ตรวจสอบว่าฟังก์ชันเป็นแบบคาบ หากคำตอบเป็นบวก ให้ศึกษาต่อเพียงช่วงระยะเวลาเดียวเท่านั้น ค้นหาจุดและกำหนดพฤติกรรมในบริเวณใกล้เคียงกับจุดเหล่านี้
ค้นหาจุดตัดของกราฟของฟังก์ชันด้วยแกนพิกัด ค้นหาพวกเขาหากมีอยู่ ใช้อนุพันธ์อันดับ 1 เพื่อตรวจสอบฟังก์ชันสำหรับช่วงสุดขั้วและช่วงความซ้ำซ้อน ทำการศึกษาโดยใช้อนุพันธ์อันดับสองสำหรับจุดนูน ความเว้า และจุดเปลี่ยนเว้า เลือกจุดเพื่อปรับแต่งฟังก์ชันและคำนวณค่าฟังก์ชันที่จุดเหล่านั้น สร้างกราฟของฟังก์ชันโดยคำนึงถึงผลลัพธ์ที่ได้จากการศึกษาทั้งหมดที่ดำเนินการ
บนแกน 0X ควรระบุจุดคุณลักษณะ: จุดไม่ต่อเนื่อง, x = 0, ศูนย์ฟังก์ชัน, จุดสุดขั้ว, จุดเปลี่ยนเว้า เส้นกำกับเหล่านี้จะให้ภาพร่างกราฟของฟังก์ชัน
ดังนั้น เมื่อใช้ตัวอย่างเฉพาะของฟังก์ชัน y=((x^2)+1)/(x-1) ให้ทำการศึกษาโดยใช้อนุพันธ์อันดับหนึ่ง เขียนฟังก์ชันใหม่เป็น y=x+1+2/(x-1) อนุพันธ์อันดับหนึ่งจะเท่ากับ y’=1-2/((x-1)^2)
ค้นหาจุดวิกฤตประเภทแรก: y’=0, (x-1)^2=2 ผลลัพธ์จะเป็นสองจุด: x1=1-sqrt2, x2=1+sqrt2 ทำเครื่องหมายค่าที่ได้รับในโดเมนของคำจำกัดความของฟังก์ชัน (รูปที่ 1)
กำหนดเครื่องหมายของอนุพันธ์ในแต่ละช่วง ตามกฎของการสลับเครื่องหมายจาก “+” ถึง “-” และจาก “-” ถึง “+” คุณจะได้ว่าจุดสูงสุดของฟังก์ชันคือ x1=1-sqrt2 และจุดต่ำสุดคือ x2=1+ sqrt2. ข้อสรุปเดียวกันนี้สามารถหาได้จากเครื่องหมายของอนุพันธ์อันดับสอง
ระดับ: 7
ฟังก์ชันนี้ถือเป็นหลักสูตรชั้นนำแห่งหนึ่งในหลักสูตรพีชคณิตของโรงเรียน และมีการนำไปประยุกต์ใช้กับวิทยาศาสตร์อื่นๆ มากมาย ในช่วงเริ่มต้นของการศึกษา เพื่อจุดประสงค์ในการจูงใจและการทำให้ประเด็นเป็นจริง ข้าพเจ้าขอแจ้งให้คุณทราบว่าไม่ใช่ปรากฏการณ์เดียวหรือกระบวนการเดียวในธรรมชาติที่สามารถศึกษาได้ ไม่มีเครื่องจักรใดที่สามารถสร้างและดำเนินการได้โดยไม่ต้องมีคำอธิบายทางคณิตศาสตร์ที่สมบูรณ์ . เครื่องมือหนึ่งสำหรับสิ่งนี้คือฟังก์ชัน การศึกษาเริ่มต้นในชั้นประถมศึกษาปีที่ 7 ตามกฎแล้วเด็ก ๆ จะไม่เจาะลึกคำจำกัดความ แนวคิดที่เข้าถึงยากเป็นพิเศษคือขอบเขตของคำจำกัดความและขอบเขตของความหมาย โดยใช้การเชื่อมโยงที่ทราบระหว่างปริมาณในปัญหาของการเคลื่อนไหวและมูลค่า ฉันแปลมันเป็นภาษาของฟังก์ชัน โดยรักษาความเชื่อมโยงกับคำจำกัดความของมัน ดังนั้นนักเรียนจึงพัฒนาแนวคิดเรื่องการทำงานในระดับจิตสำนึก ในขั้นตอนเดียวกัน การทำงานอย่างอุตสาหะจะดำเนินการกับแนวคิดใหม่: โดเมนของคำจำกัดความ, โดเมนของค่า, อาร์กิวเมนต์, ค่าของฟังก์ชัน ฉันใช้การเรียนรู้ขั้นสูง: ฉันแนะนำสัญกรณ์ D(y), E(y) แนะนำแนวคิดของศูนย์ของฟังก์ชัน (เชิงวิเคราะห์และกราฟิก) เมื่อแก้แบบฝึกหัดที่มีพื้นที่ที่มีเครื่องหมายคงที่ ยิ่งนักเรียนต้องเผชิญกับแนวคิดที่ยากขึ้นเร็วและบ่อยขึ้นเท่าใด พวกเขาก็จะยิ่งตระหนักรู้ถึงแนวคิดเหล่านั้นในระดับความจำระยะยาวได้ดีขึ้นเท่านั้น เมื่อศึกษาฟังก์ชันเชิงเส้น แนะนำให้แสดงความเชื่อมโยงกับคำตอบของสมการและระบบเชิงเส้น และต่อมากับคำตอบของอสมการเชิงเส้นและระบบของพวกมัน ในการบรรยาย นักเรียนจะได้รับข้อมูลใหม่จำนวนมาก (โมดูล) ดังนั้นในตอนท้ายของการบรรยาย เนื้อหาจะถูก "ตัดออก" และจะมีการรวบรวมบทสรุปที่นักเรียนต้องรู้ ทักษะการปฏิบัติได้รับการพัฒนาในกระบวนการฝึกหัดโดยใช้วิธีการต่าง ๆ ซึ่งขึ้นอยู่กับงานส่วนบุคคลและงานอิสระ
1. ข้อมูลบางอย่างเกี่ยวกับฟังก์ชันเชิงเส้น
ฟังก์ชันเชิงเส้นมักพบบ่อยมากในทางปฏิบัติ ความยาวของแกนเป็นฟังก์ชันเชิงเส้นของอุณหภูมิ ความยาวของรางและสะพานก็เป็นฟังก์ชันเชิงเส้นของอุณหภูมิเช่นกัน ระยะทางที่คนเดินเท้า รถไฟ หรือรถยนต์เดินทางด้วยความเร็วคงที่นั้นเป็นฟังก์ชันเชิงเส้นของเวลาเดินทาง
ฟังก์ชันเชิงเส้นอธิบายความสัมพันธ์ทางกายภาพและกฎจำนวนหนึ่ง ลองดูบางส่วนของพวกเขา
1) l = l о (1+at) – การขยายตัวเชิงเส้นของของแข็ง
2) v = v о (1+bt) – การขยายตัวเชิงปริมาตรของของแข็ง
3) p=p o (1+at) – การขึ้นอยู่กับความต้านทานของตัวนำที่เป็นของแข็งกับอุณหภูมิ
4) v = v o + at – ความเร็วของการเคลื่อนที่ที่มีความเร่งสม่ำเสมอ
5) x= x o + vt – พิกัดของการเคลื่อนที่สม่ำเสมอ
ภารกิจที่ 1 กำหนดฟังก์ชันเชิงเส้นจากข้อมูลแบบตาราง:
| เอ็กซ์ | 1 | 3 |
| ที่ | -1 | 3 |
สารละลาย. y= kx+b ปัญหาลดลงเหลือเพียงการแก้ระบบสมการ: 1=k 1+b และ 3=k 3 + b
คำตอบ: y = 2x – 3
ปัญหาที่ 2 การเคลื่อนที่สม่ำเสมอและเป็นเส้นตรง ร่างกายผ่านไป 14 เมตรใน 8 วินาทีแรก และ 12 เมตรในอีก 4 วินาที สร้างสมการการเคลื่อนที่โดยอาศัยข้อมูลเหล่านี้
สารละลาย. ตามเงื่อนไขของปัญหาเรามีสมการสองสมการ: 14 = x o +8 v o และ 26 = x o +12 v o การแก้ระบบสมการเราได้ v = 3, x o = -10
คำตอบ: x = -10 + 3t
ปัญหาที่ 3. รถยนต์คันหนึ่งออกจากเมืองเคลื่อนที่ด้วยความเร็ว 80 กม./ชม. ผ่านไป 1.5 ชั่วโมง ก็มีมอเตอร์ไซค์คันหนึ่งตามมาด้วยความเร็ว 100 กม./ชม. มอเตอร์ไซค์อีกนานเท่าไหร่ถึงจะตามทัน? สิ่งนี้จะเกิดขึ้นที่ระยะทางจากเมืองเท่าใด?
คำตอบ: 7.5 ชั่วโมง 600 กม.
ภารกิจที่ 4ระยะห่างระหว่างจุดสองจุดในช่วงเวลาเริ่มต้นคือ 300 เมตร จุดเคลื่อนที่เข้าหากันด้วยความเร็ว 1.5 m/s และ 3.5 m/s พวกเขาจะพบกันเมื่อไหร่? สิ่งนี้จะเกิดขึ้นที่ไหน?
คำตอบ: 60 วิ 90 ม.
ภารกิจที่ 5ไม้บรรทัดทองแดงที่อุณหภูมิ 0 o C มีความยาว 1 เมตร ค้นหาความยาวที่เพิ่มขึ้นเมื่ออุณหภูมิเพิ่มขึ้น 35 o, 1,000 o C (จุดหลอมเหลวของทองแดงคือ 1,083 o C)
คำตอบ: 0.6 มม.
2. สัดส่วนโดยตรง
กฎฟิสิกส์หลายข้อแสดงออกมาผ่านสัดส่วนโดยตรง ในกรณีส่วนใหญ่ แบบจำลองจะใช้ในการเขียนกฎหมายเหล่านี้
ในบางกรณี -
ลองยกตัวอย่างบางส่วน
1. S = โวลต์ เสื้อ (v – const)
2. v = a t (a – const, a – ความเร่ง)
3. F = kx (กฎของฮุค: F – แรง, k – ความแข็ง (const), x – การยืดตัว)
4. E= F/q (E คือความเข้ม ณ จุดที่กำหนดของสนามไฟฟ้า, E คือ const, F คือแรงที่กระทำต่อประจุ, q คือขนาดของประจุ)
ในฐานะที่เป็นแบบจำลองทางคณิตศาสตร์ของสัดส่วนโดยตรง คุณสามารถใช้ความคล้ายคลึงกันของสามเหลี่ยมหรือสัดส่วนของเซกเมนต์ได้ (ทฤษฎีบทของทาเลส)
ปัญหาที่ 1 รถไฟผ่านสัญญาณไฟจราจรใน 5 วินาที และผ่านชานชาลายาว 150 เมตร ใน 15 วินาที รถไฟมีความยาวเท่าไรและมีความเร็วเท่าไร?
สารละลาย. ให้ x เป็นความยาวของรถไฟ x+150 เป็นความยาวรวมของรถไฟและชานชาลา ในปัญหานี้ ความเร็วจะคงที่ และเวลาเป็นสัดส่วนกับความยาว
เรามีสัดส่วน: (x+150) :15 = x: 5
โดยที่ x = 75, v = 15
คำตอบ. 75 ม., 15 ม./วินาที
ปัญหาที่ 2 เรือล่องไปตามกระแสน้ำเป็นระยะทาง 90 กม. ในช่วงเวลาหนึ่ง ในช่วงเวลาเดียวกัน เขาจะเดินทางทวนกระแสน้ำเป็นระยะทาง 70 กม. ช่วงนี้แพจะเดินทางได้ไกลแค่ไหน?
คำตอบ. 10 กม.
ปัญหาที่ 3. อุณหภูมิเริ่มต้นของอากาศจะเป็นเท่าใด หากได้รับความร้อน 3 องศา ปริมาตรเพิ่มขึ้น 1% ของอุณหภูมิเดิม
คำตอบ. 300 K (เคลวิน) หรือ 27 0 C
การบรรยายในหัวข้อ "ฟังก์ชันเชิงเส้น"
พีชคณิต ชั้นประถมศึกษาปีที่ 7
1. พิจารณาตัวอย่างปัญหาโดยใช้สูตรที่รู้จักกันดี:
S = v t (สูตรเส้นทาง), (1)
C = ck (สูตรค่า) (2)
ปัญหาที่ 1 รถขับไป 20 กม. จากจุด A และเดินทางต่อด้วยความเร็ว 62 กม./ชม. ระยะทางจากจุด A รถจะอยู่ห่างจากจุด A เท่าใดหลังจาก t ชั่วโมง? สร้างนิพจน์ของปัญหาแทนระยะทาง S หาได้ที่ t = 1 ชั่วโมง 2.5 ชั่วโมง 4 ชั่วโมง
1) จากสูตร (1) เราจะหาเส้นทางที่รถยนต์เคลื่อนที่ด้วยความเร็ว 62 กม./ชม. ในเวลา t, S 1 = 62t;
2) จากนั้นจากจุด A หลังจาก t ชั่วโมง รถจะอยู่ที่ระยะทาง S = S 1 + 20 หรือ S = 62t + 20 ลองหาค่าของ S:
ที่ เสื้อ = 1, S = 62*1 + 20, S = 82;
ที่ เสื้อ = 2.5, S = 62*2.5 + 20, S = 175;
ที่ t = 4, S = 62*4+ 20, S = 268
เราสังเกตว่าเมื่อค้นหา S เฉพาะค่าของ t และ S เท่านั้นที่เปลี่ยนแปลง กล่าวคือ t และ S เป็นตัวแปร และ S ขึ้นอยู่กับ t แต่ละค่าของ t สอดคล้องกับค่าเดียวของ S โดยแสดงถึงตัวแปร S ด้วย Y และ t ด้วย x เราได้รับสูตรสำหรับการแก้ปัญหานี้:
Y= 62x + 20. (3)
ปัญหาที่ 2 ในร้านค้าเราซื้อหนังสือเรียนราคา 150 รูเบิลและสมุดบันทึก 15 เล่มราคา n รูเบิลต่อเล่ม คุณจ่ายเงินเท่าไรในการซื้อ? เขียนนิพจน์สำหรับปัญหา โดยแทนต้นทุน C หาได้สำหรับ n = 5,8,16
1) การใช้สูตร (2) เราค้นหาต้นทุนของโน้ตบุ๊ก C 1 = 15n;
2) จากนั้นต้นทุนของการซื้อทั้งหมดคือ C = C 1 +150 หรือ C = 15n+150 ลองหาค่าของ C:
โดยที่ n = 5, C = 15 5 + 150, C = 225;
โดยที่ n = 8, C = 15 8 + 150, C = 270;
โดยที่ n = 16, C = 15 16+ 150, C = 390
ในทำนองเดียวกัน เราสังเกตว่า C และ n เป็นตัวแปร สำหรับแต่ละค่าของ n จะมีค่าเดียวของ C แสดงว่าตัวแปร C เป็น Y และ n เป็น x เราจะได้สูตรสำหรับการแก้ปัญหา 2:
Y= 15x + 150 (4)
เมื่อเปรียบเทียบสูตร (3) และ (4) เรามั่นใจว่าตัวแปร Y พบผ่านตัวแปร x โดยใช้อัลกอริทึมเดียวกัน เราพิจารณาเพียงสองปัญหาที่แตกต่างกันซึ่งอธิบายปรากฏการณ์ที่ล้อมรอบเราทุกวัน ในความเป็นจริง มีกระบวนการมากมายที่เปลี่ยนแปลงไปตามกฎหมายที่ได้รับ ดังนั้นการพึ่งพาระหว่างตัวแปรดังกล่าวจึงสมควรได้รับการศึกษา
วิธีแก้ไขปัญหาแสดงให้เห็นว่าค่าของตัวแปร x ถูกเลือกโดยพลการซึ่งเป็นไปตามเงื่อนไขของปัญหา (บวกในปัญหา 1 และเป็นธรรมชาติในปัญหา 2) เช่น x เป็นตัวแปรอิสระ (เรียกว่าอาร์กิวเมนต์) และ Y เป็นตัวแปรตามและมีการโต้ตอบแบบหนึ่งต่อหนึ่งระหว่างตัวแปรเหล่านั้น และตามคำจำกัดความแล้ว การพึ่งพาดังกล่าวถือเป็นฟังก์ชัน ดังนั้นเราจึงแสดงค่าสัมประสิทธิ์ของ x ด้วยตัวอักษร k และเทอมอิสระด้วยตัวอักษร b เราได้สูตร
Y= kx + ข
ความหมาย: หน้าที่ของแบบฟอร์ม y= kx + ขโดยที่ k, b คือตัวเลขบางตัว x คืออาร์กิวเมนต์ y คือค่าของฟังก์ชัน เรียกว่าฟังก์ชันเชิงเส้น
เพื่อศึกษาคุณสมบัติของฟังก์ชันเชิงเส้น เราจะแนะนำคำจำกัดความ
คำจำกัดความ 1 ชุดของค่าที่ยอมรับได้ของตัวแปรอิสระเรียกว่าโดเมนของคำจำกัดความของฟังก์ชัน (ยอมรับได้ - นี่หมายถึงค่าตัวเลขของ x ที่ทำการคำนวณ y) และแสดงแทน D(y)
คำจำกัดความ 2 ชุดของค่าของตัวแปรตามเรียกว่าโดเมนของฟังก์ชัน (นี่คือค่าตัวเลขที่ y รับ) และแสดงแทน E(y)
คำจำกัดความ 3 กราฟของฟังก์ชันคือเซตของจุดบนระนาบพิกัดซึ่งพิกัดจะเปลี่ยนสูตรให้มีความเท่าเทียมกันอย่างแท้จริง
คำจำกัดความ 4. ค่าสัมประสิทธิ์ k ของ x เรียกว่าความชัน
ลองพิจารณาคุณสมบัติของฟังก์ชันเชิงเส้นกัน
1. D(y) – ตัวเลขทั้งหมด (การคูณกำหนดไว้ที่เซตของตัวเลขทั้งหมด)
2. E(y) – ตัวเลขทั้งหมด
3. ถ้า y = 0 แล้ว x = -b/k จุด (-b/k;0) – จุดตัดกับแกน Ox เรียกว่าศูนย์ของฟังก์ชัน
4. ถ้า x = 0 แล้ว y = b จุด (0; b) คือจุดตัดกับแกน Oy
5. มาดูกันว่าฟังก์ชันเชิงเส้นบนระนาบพิกัดเส้นใดจะเรียงตามจุดต่างๆ เช่น ซึ่งเป็นกราฟของฟังก์ชัน เมื่อต้องการทำเช่นนี้ ให้พิจารณาฟังก์ชันต่างๆ
1) y= 2x + 3, 2) y= -3x – 2
เราจะสร้างตารางค่าสำหรับแต่ละฟังก์ชัน มาตั้งค่าที่กำหนดเองของตัวแปร x และคำนวณค่าที่สอดคล้องกันของตัวแปร Y
| เอ็กซ์ | -1,5 | -2 | 0 | 1 | 2 |
| ย | 0 | -1 | 3 | 5 | 7 |

เมื่อสร้างคู่ผลลัพธ์ (x;y) บนระนาบพิกัดและเชื่อมต่อพวกมันสำหรับแต่ละฟังก์ชันแยกกัน (เราใช้ค่า x ด้วยขั้นตอนที่ 1 ถ้าเราลดขั้นตอน จุดต่างๆ จะเรียงกันบ่อยขึ้น และ หากขั้นตอนใกล้กับศูนย์ จุดจะรวมกันเป็นเส้นทึบ ) เราจะสังเกตเห็นว่าจุดเรียงกันเป็นเส้นตรงในกรณีที่ 1) และในกรณีที่ 2) เนื่องจากความจริงที่ว่าฟังก์ชั่นถูกเลือกโดยพลการ (สร้างกราฟด้วยตัวเอง y= 0.5x – 4, y= x + 5) เราจึงสรุปได้ว่า ว่ากราฟของฟังก์ชันเชิงเส้นเป็นเส้นตรง- การใช้คุณสมบัติของเส้นตรง: มีเพียงเส้นตรงเส้นเดียวที่ผ่านจุดสองจุด ก็เพียงพอแล้วที่จะใช้สองจุดเพื่อสร้างเส้นตรง
6. จากเรขาคณิต เป็นที่ทราบกันดีว่าเส้นสามารถตัดกันหรือขนานกันก็ได้ เรามาศึกษาตำแหน่งสัมพัทธ์ของกราฟของฟังก์ชันต่างๆ กัน
1) y= -x + 5, y= -x + 3, y= -x – 4; 2) y= 2x + 2, y= x + 2, y= -0.5x + 2
มาสร้างกลุ่มกราฟ 1) และ 2) แล้วสรุปผล
|
 |
กราฟของฟังก์ชัน 1) วางขนานกันเมื่อตรวจสอบสูตร เราสังเกตว่าฟังก์ชันทั้งหมดมีค่าสัมประสิทธิ์ x เท่ากัน
กราฟของฟังก์ชัน 2) ตัดกันที่จุดหนึ่ง (0;2) จากการตรวจสอบสูตร เราสังเกตเห็นว่าค่าสัมประสิทธิ์แตกต่างกัน และตัวเลข b = 2
นอกจากนี้ จะสังเกตเห็นได้ง่ายว่าเส้นตรงที่กำหนดโดยฟังก์ชันเชิงเส้นที่มี k › 0 ทำให้เกิดมุมแหลมโดยมีทิศทางบวกของแกน Ox และมุมป้านที่มี k ‹ 0 ดังนั้นค่าสัมประสิทธิ์ k จึงเรียกว่าค่าสัมประสิทธิ์ความชัน
7. ลองพิจารณากรณีพิเศษของฟังก์ชันเชิงเส้น ขึ้นอยู่กับค่าสัมประสิทธิ์
1) ถ้า b=0 ฟังก์ชันจะอยู่ในรูปแบบ y= kx แล้ว k = y/x (อัตราส่วนจะแสดงจำนวนครั้งของความแตกต่าง หรือส่วน y มาจาก x)
ฟังก์ชันที่อยู่ในรูปแบบ Y= kx เรียกว่า สัดส่วนโดยตรง ฟังก์ชันนี้มีคุณสมบัติทั้งหมดของฟังก์ชันเชิงเส้น ลักษณะพิเศษของมันคือสำหรับ x=0 y=0 กราฟสัดส่วนโดยตรงจะผ่านจุดกำเนิด (0;0)
2) ถ้า k = 0 ฟังก์ชันจะอยู่ในรูปแบบ y = b ซึ่งหมายความว่าสำหรับค่าใด ๆ ของ x ฟังก์ชันจะใช้ค่าเดียวกัน
ฟังก์ชันที่อยู่ในรูปแบบ y = b เรียกว่าค่าคงที่ กราฟของฟังก์ชันเป็นเส้นตรงที่ลากผ่านจุด (0;b) ขนานกับแกน Ox ที่ b=0 กราฟของฟังก์ชันคงที่เกิดขึ้นพร้อมกับแกน abscissa
เชิงนามธรรม
1. คำนิยาม ฟังก์ชันที่อยู่ในรูปแบบ Y = kx + b โดยที่ k, b คือตัวเลขจำนวนหนึ่ง x คืออาร์กิวเมนต์ Y คือค่าของฟังก์ชัน เรียกว่าฟังก์ชันเชิงเส้น
D(y) – ตัวเลขทั้งหมด
E(y) – ตัวเลขทั้งหมด
กราฟของฟังก์ชันเชิงเส้นคือเส้นตรงที่ผ่านจุด (0;b)
2. ถ้า b=0 ฟังก์ชันจะอยู่ในรูปแบบ y= kx เรียกว่า สัดส่วนโดยตรง กราฟสัดส่วนตรงจะผ่านจุดกำเนิด
3. ถ้า k = 0 ฟังก์ชันจะอยู่ในรูปแบบ y= b เรียกว่าค่าคงที่ กราฟของฟังก์ชันคงที่ผ่านจุด (0;b) ขนานกับแกนแอบซิสซา
4. การจัดเรียงกราฟของฟังก์ชันเชิงเส้นเชิงสัมพันธ์
กำหนดให้ฟังก์ชัน y= k 1 x + b 1 และ y= k 2 x + b 2
ถ้า k 1 = k 2 กราฟจะขนานกัน
ถ้า k 1 และ k 2 ไม่เท่ากัน กราฟจะตัดกัน
5. ดูตัวอย่างกราฟของฟังก์ชันเชิงเส้นด้านบน
วรรณกรรม.
- หนังสือเรียน Yu.N. มาคารีเชฟ, N.G. มินดุ๊ก, K.I. เนชคอฟและคนอื่นๆ “พีชคณิต 8”
- สื่อการสอนเกี่ยวกับพีชคณิตสำหรับเกรด 8 / V.I. Zhokhov, Yu.N. มาคารีเชฟ, N.G. มินดุ๊ก. – อ.: การศึกษา, 2549 – 144 น.
- ภาคผนวกของหนังสือพิมพ์ 1 กันยายน “คณิตศาสตร์”, 2544, ฉบับที่ 2, ฉบับที่ 4.
มาสโลวา แองเจลิน่า
งานวิจัยทางคณิตศาสตร์ แองเจลินารวบรวมแบบจำลองคอมพิวเตอร์ของฟังก์ชันเชิงเส้นซึ่งเธอใช้ในการทำวิจัย
ดาวน์โหลด:
ดูตัวอย่าง:
สถาบันการศึกษาอิสระของเทศบาล โรงเรียนมัธยมหมายเลข 8 ของเขตเมือง Bor ภูมิภาค Nizhny Novgorod
งานวิจัยทางวิทยาการคอมพิวเตอร์และคณิตศาสตร์
สำเร็จโดยนักเรียนคลาส 7A Angelina Maslova
หัวหน้า: ครูสอนวิทยาศาสตร์คอมพิวเตอร์ Voronina Anna Alekseevna
เขตเมืองบ่อ - 2558
การแนะนำ
- การสำรวจฟังก์ชันเชิงเส้นในสเปรดชีต
บทสรุป
บรรณานุกรม
การแนะนำ
ปีนี้ในบทเรียนพีชคณิต เราได้รู้จักฟังก์ชันเชิงเส้น เราเรียนรู้ที่จะสร้างกราฟของฟังก์ชันเชิงเส้น โดยพิจารณาว่ากราฟของฟังก์ชันควรมีลักษณะอย่างไรโดยขึ้นอยู่กับค่าสัมประสิทธิ์ของมัน หลังจากนั้นไม่นาน ในบทเรียนวิทยาการคอมพิวเตอร์ เราได้เรียนรู้ว่าการกระทำเหล่านี้ถือได้ว่าเป็นการสร้างแบบจำลองทางคณิตศาสตร์ ฉันตัดสินใจว่าจะสำรวจฟังก์ชันเชิงเส้นโดยใช้สเปรดชีตได้หรือไม่
เป้าหมายของงาน: สำรวจฟังก์ชันเชิงเส้นในสเปรดชีต
วัตถุประสงค์ของการวิจัย:
- ค้นหาและศึกษาข้อมูลเกี่ยวกับฟังก์ชันเชิงเส้น
- สร้างแบบจำลองทางคณิตศาสตร์ของฟังก์ชันเชิงเส้นในสเปรดชีต
- สำรวจฟังก์ชันเชิงเส้นโดยใช้แบบจำลองที่สร้างขึ้น
วัตถุประสงค์ของการศึกษา:การสร้างแบบจำลองทางคณิตศาสตร์
หัวข้อการศึกษา:แบบจำลองทางคณิตศาสตร์ของฟังก์ชันเชิงเส้น
การสร้างแบบจำลองเป็นวิธีการรับรู้
บุคคลสัมผัสโลกเกือบตั้งแต่เกิด ในการทำเช่นนี้บุคคลจะใช้แบบจำลองที่มีความหลากหลายมาก
แบบอย่าง เป็นวัตถุใหม่ที่สะท้อนคุณสมบัติที่สำคัญบางประการของวัตถุจริง
แบบจำลองของวัตถุจริงถูกนำมาใช้ในสถานการณ์ต่างๆ:
- เมื่อวัตถุมีขนาดใหญ่มาก (เช่น โลกเป็นแบบจำลอง: ลูกโลกหรือแผนที่) หรือในทางกลับกัน เล็กเกินไป (เซลล์ชีวภาพ)
- เมื่อวัตถุมีโครงสร้างที่ซับซ้อนมาก (รถ - รุ่น: รถเด็ก)
- เมื่อวัตถุมีอันตรายต่อการศึกษา (ภูเขาไฟ)
- เมื่อวัตถุอยู่ไกลมาก
การสร้างแบบจำลอง เป็นกระบวนการสร้างและศึกษาแบบจำลอง
เราสร้างและใช้โมเดลด้วยตัวเอง บางครั้งโดยไม่ได้คิดถึงมันเลย ตัวอย่างเช่น เราถ่ายรูปเหตุการณ์บางอย่างในชีวิตของเราแล้วแสดงให้เพื่อนๆ ของเราดู
ขึ้นอยู่กับประเภทของข้อมูล ทุกรุ่นสามารถแบ่งออกเป็นหลายกลุ่ม:
- โมเดลวาจา โมเดลเหล่านี้อาจมีอยู่ในรูปแบบวาจาหรือลายลักษณ์อักษรก็ได้ อาจเป็นเพียงคำอธิบายด้วยวาจาของวัตถุหรือบทกวี หรืออาจเป็นบทความในหนังสือพิมพ์หรือเรียงความ ทั้งหมดนี้เป็นเพียงแบบจำลองทางวาจา
- โมเดลกราฟิก นี่คือภาพวาด ภาพถ่าย ไดอะแกรม และกราฟของเรา
- โมเดลอันเป็นเอกลักษณ์ เหล่านี้เป็นแบบจำลองที่เขียนด้วยภาษาสัญลักษณ์บางภาษา: บันทึกย่อ สูตรทางคณิตศาสตร์ ฟิสิกส์ หรือเคมี
ฟังก์ชันเชิงเส้นและคุณสมบัติของมัน
ฟังก์ชันเชิงเส้นเรียกว่าฟังก์ชันของแบบฟอร์ม
กราฟของฟังก์ชันเชิงเส้นจะเป็นเส้นตรง
1 - เพื่อพล็อตฟังก์ชันเราต้องการพิกัดของจุดสองจุดที่เป็นของกราฟของฟังก์ชัน ในการค้นหา คุณต้องนำค่า x สองค่ามาแทนที่ลงในสมการของฟังก์ชัน และใช้ค่าเหล่านี้ในการคำนวณค่า y ที่สอดคล้องกัน
ตัวอย่างเช่น เพื่อพล็อตฟังก์ชันสะดวกในการพกพาและ แล้วพิกัดของจุดเหล่านี้จะเท่ากันและ .
เราได้คะแนน A(0;2) และ B(3;3) ลองเชื่อมต่อพวกมันและรับกราฟของฟังก์ชันกัน:

2 - ในสมการของฟังก์ชัน y=kx+b ค่าสัมประสิทธิ์ k รับผิดชอบต่อความชันของกราฟฟังก์ชัน:
ค่าสัมประสิทธิ์ b มีหน้าที่ในการเลื่อนกราฟไปตามแกน OY:
รูปด้านล่างแสดงกราฟของฟังก์ชัน; ;

โปรดทราบว่าในฟังก์ชันทั้งหมดเหล่านี้จะมีค่าสัมประสิทธิ์มากกว่าศูนย์ไปทางขวา - อีกทั้งยิ่งมีมูลค่ามากขึ้นยิ่งเส้นตรงชันมากเท่าไร
ในทุกฟังก์ชั่น– และเราเห็นว่ากราฟทั้งหมดตัดแกน OY ที่จุด (0;3)
ทีนี้มาดูกราฟของฟังก์ชันกัน; ;

คราวนี้ในทุกฟังก์ชันจะมีค่าสัมประสิทธิ์น้อยกว่าศูนย์ และกราฟฟังก์ชันทั้งหมดมีความลาดเอียงซ้าย - ค่าสัมประสิทธิ์ b เท่ากัน b=3 และกราฟตัดแกน OY ที่จุด (0;3) เช่นเดียวกับในกรณีก่อนหน้านี้
ลองดูกราฟของฟังก์ชันกัน; ;

ตอนนี้ในสมการฟังก์ชันทั้งหมดจะมีค่าสัมประสิทธิ์มีความเท่าเทียมกัน และเราได้เส้นขนานสามเส้น
แต่ค่าสัมประสิทธิ์ b ต่างกัน และกราฟเหล่านี้ตัดแกน OY ที่จุดต่างกัน:
กราฟของฟังก์ชัน (b=3) ตัดแกน OY ที่จุด (0;3)
กราฟของฟังก์ชัน (b=0) ตัดแกน OY ที่จุด (0;0) - จุดกำเนิด
กราฟของฟังก์ชัน (b=-2) ตัดแกน OY ที่จุด (0;-2)
ดังนั้น หากเรารู้สัญญาณของสัมประสิทธิ์ k และ b เราก็สามารถจินตนาการได้ทันทีว่ากราฟของฟังก์ชันจะเป็นอย่างไร.
ถ้า k 0 แล้วกราฟของฟังก์ชันมีรูปแบบ:

ถ้า k>0 และ b>0 , แล้วกราฟของฟังก์ชันมีรูปแบบ:

ถ้า k>0 และ b , แล้วกราฟของฟังก์ชันมีรูปแบบ:

ถ้าเค แล้วกราฟของฟังก์ชันมีรูปแบบ:

ถ้า k=0 แสดงว่าฟังก์ชัน กลายเป็นฟังก์ชันและกราฟของมันจะเป็นดังนี้:

พิกัดของจุดทั้งหมดบนกราฟของฟังก์ชันเท่ากัน
ถ้าข=0 แล้วกราฟของฟังก์ชันผ่านแหล่งกำเนิด:

4. เงื่อนไขความขนานของเส้นสองเส้น:
กราฟของฟังก์ชัน ขนานกับกราฟของฟังก์ชัน, ถ้า
5. เงื่อนไขของการตั้งฉากของเส้นตรงสองเส้น:
กราฟของฟังก์ชัน ตั้งฉากกับกราฟของฟังก์ชัน, เพื่อ
6 - จุดตัดของกราฟฟังก์ชันด้วยแกนพิกัด
ด้วยแกน OY ค่า Abscissa ของจุดใดๆ ที่เป็นของแกน OY มีค่าเท่ากับศูนย์ ดังนั้น หากต้องการหาจุดตัดกับแกน OY คุณต้องแทนที่ศูนย์ในสมการของฟังก์ชันแทน x เราได้ y=b นั่นคือจุดตัดกับแกน OY มีพิกัด (0; b)
ด้วยแกน OX: พิกัดของจุดใดๆ ที่เป็นของแกน OX มีค่าเท่ากับศูนย์ ดังนั้น หากต้องการหาจุดตัดกับแกน OX คุณต้องแทนที่ศูนย์ในสมการของฟังก์ชันแทน y เราได้ 0=kx+b จากที่นี่- นั่นคือจุดตัดกับแกน OX มีพิกัด (;0):

การสำรวจฟังก์ชันเชิงเส้นในสเปรดชีต
เพื่อศึกษาฟังก์ชันเชิงเส้นในสภาพแวดล้อมสเปรดชีต ฉันได้รวบรวมอัลกอริทึมต่อไปนี้:
- สร้างแบบจำลองทางคณิตศาสตร์ของฟังก์ชันเชิงเส้นในสเปรดชีต
- กรอกตารางการติดตามของอาร์กิวเมนต์และค่าฟังก์ชัน
- พล็อตฟังก์ชันเชิงเส้นโดยใช้ตัวช่วยสร้างแผนภูมิ
- สำรวจฟังก์ชันเชิงเส้นขึ้นอยู่กับค่าของสัมประสิทธิ์
เพื่อศึกษาฟังก์ชันเชิงเส้น ฉันใช้ Microsoft Office Excel 2007 ฉันใช้สูตรเพื่อรวบรวมตารางอาร์กิวเมนต์และค่าฟังก์ชัน ฉันได้รับตารางค่าต่อไปนี้:
เมื่อใช้แบบจำลองทางคณิตศาสตร์ดังกล่าว คุณสามารถตรวจสอบการเปลี่ยนแปลงในกราฟของฟังก์ชันเชิงเส้นได้อย่างง่ายดายโดยการเปลี่ยนค่าสัมประสิทธิ์ในตาราง
นอกจากนี้ เมื่อใช้สเปรดชีต ฉันตัดสินใจติดตามว่าตำแหน่งสัมพัทธ์ของกราฟของฟังก์ชันเชิงเส้นสองฟังก์ชันเปลี่ยนแปลงไปอย่างไร หลังจากสร้างแบบจำลองทางคณิตศาสตร์ใหม่ในสเปรดชีต ฉันได้ผลลัพธ์ดังต่อไปนี้:
ด้วยการเปลี่ยนค่าสัมประสิทธิ์ของฟังก์ชันเชิงเส้นสองฟังก์ชัน ฉันมั่นใจได้อย่างชัดเจนถึงความถูกต้องของข้อมูลที่ฉันได้เรียนรู้เกี่ยวกับคุณสมบัติของฟังก์ชันเชิงเส้น
บทสรุป
ฟังก์ชันเชิงเส้นในพีชคณิตถือว่าง่ายที่สุด แต่ในขณะเดียวกันก็มีคุณสมบัติหลายอย่างที่ไม่ชัดเจนในทันที หลังจากสร้างแบบจำลองทางคณิตศาสตร์ของฟังก์ชันเชิงเส้นในสเปรดชีตและตรวจสอบแล้ว คุณสมบัติของฟังก์ชันเชิงเส้นก็ชัดเจนมากขึ้นสำหรับฉัน ฉันสามารถเห็นได้อย่างชัดเจนว่ากราฟเปลี่ยนแปลงอย่างไรเมื่อค่าสัมประสิทธิ์ของฟังก์ชันเปลี่ยนไป
ฉันคิดว่าแบบจำลองทางคณิตศาสตร์ที่ฉันสร้างขึ้นจะช่วยให้นักเรียนชั้นประถมศึกษาปีที่ 7 สำรวจฟังก์ชันเชิงเส้นได้อย่างอิสระและเข้าใจได้ดีขึ้น
บรรณานุกรม
- หนังสือเรียนพีชคณิตสำหรับชั้นประถมศึกษาปีที่ 7
- หนังสือเรียนวิทยาการคอมพิวเตอร์สำหรับชั้นประถมศึกษาปีที่ 7
- วิกิพีเดีย.org
ดูตัวอย่าง:
หากต้องการใช้ตัวอย่างการนำเสนอ ให้สร้างบัญชี Google และเข้าสู่ระบบ: https://accounts.google.com
คำอธิบายสไลด์:
วัตถุประสงค์ของการศึกษา: ฟังก์ชันเชิงเส้น หัวข้อวิจัย: แบบจำลองทางคณิตศาสตร์ของฟังก์ชันเชิงเส้น
วัตถุประสงค์ของงาน: เพื่อตรวจสอบฟังก์ชันเชิงเส้นในสเปรดชีต วัตถุประสงค์การวิจัย: เพื่อค้นหาและศึกษาข้อมูลเกี่ยวกับฟังก์ชันเชิงเส้น สร้างแบบจำลองทางคณิตศาสตร์ของฟังก์ชันเชิงเส้นในสเปรดชีต สำรวจฟังก์ชันเชิงเส้นโดยใช้แบบจำลองที่สร้างขึ้น
ฟังก์ชันเชิงเส้นคือฟังก์ชันที่อยู่ในรูปแบบ y= k x+ b โดยที่ x คืออาร์กิวเมนต์ และ k และ b คือตัวเลขจำนวนหนึ่ง (สัมประสิทธิ์) กราฟของฟังก์ชันเชิงเส้นจะเป็นเส้นตรง
พิจารณาฟังก์ชัน y=kx+b โดยที่ k 0 , b=0 ดู: y=kx ในระบบพิกัดเดียว เราจะสร้างกราฟของฟังก์ชันเหล่านี้: y=3x y=x y=-7x เราจะสร้างแต่ละกราฟด้วยสีที่สอดคล้องกัน x 0 1 y 0 3 x 0 1 y 0 1 x 0 1 ใช่ 0 7
กราฟของฟังก์ชันเชิงเส้นในรูปแบบ y = k x ผ่านจุดกำเนิด y=x y=3x y=-7x y x
สรุป: กราฟของฟังก์ชันเชิงเส้นในรูปแบบ y = kx + b ตัดกับแกน O Y ที่จุด (0; b)
พิจารณาฟังก์ชัน y=kx+b โดยที่ k=0 ดู: y=b ในระบบพิกัดเดียว สร้างกราฟของฟังก์ชัน: y=4 y=-3 y=0 เราสร้างแต่ละกราฟด้วยสีที่เหมาะสม
กราฟของฟังก์ชันเชิงเส้นในรูปแบบ y = b วิ่งขนานกับแกน OX และตัดแกน O Y ที่จุด (0; b) y=4 y=-3 y=0 yx
ในระบบพิกัดเดียว สร้างกราฟของฟังก์ชัน: Y=2x Y=2x+ 3 Y=2x-4 เราสร้างแต่ละกราฟด้วยสีที่เหมาะสม x 0 1 y 0 2 x 0 1 y 3 5 x 0 1 y -4 -2
กราฟของฟังก์ชันเชิงเส้นในรูปแบบ y=kx+b จะขนานกันถ้าสัมประสิทธิ์ของ x เท่ากัน y =2x+ 3 y =2x y =2x-4 yx
ในระบบพิกัดหนึ่ง เราจะสร้างกราฟของฟังก์ชัน: y=3x+4 Y= - 2x+4 เราจะสร้างกราฟด้วยสีที่เหมาะสม x 0 1 y 4 7 x 0 1 y 4 2
กราฟของฟังก์ชันเชิงเส้นสองฟังก์ชันในรูปแบบ y=kx+b จะตัดกันหากสัมประสิทธิ์ของ x ต่างกัน ใช่
ในระบบพิกัดหนึ่ง เราจะสร้างกราฟของฟังก์ชัน: y=0, 5x-2 y=-2x-4 y= 4 x-1 y=- 0, 2 5 x- 3 x 0 4 y x 0 -2 y -4 0 x 0 4 ปี -2 0 x 0 1 ปี -1 3 x 0 - 4 ปี -3 -2
y=0, 5x-2 y=-2x-4 y= 4 x-1 y=- 0, 2 5 x- 3 กราฟของฟังก์ชันเชิงเส้นตรงสองฟังก์ชันในรูปแบบ y=kx+b จะตั้งฉากกัน ถ้าผลคูณของ ค่าสัมประสิทธิ์ของ x คือ “ - 1" .
ดังนั้นค่าสัมประสิทธิ์ k จึงเรียกว่าความชันของเส้นตรง - กราฟของฟังก์ชัน y=kx+ b ถ้า k 0 มุมเอียงของกราฟกับแกน O X จะเป็นมุมแหลม ฟังก์ชั่นเพิ่มขึ้น ใช่ x ใช่ x
สเปรดชีต
สเปรดชีต
สมการเชิงเส้น เงื่อนไขพีชคณิต อนุพันธ์ทางเรขาคณิต y = k 1 x+ b 1 k 1 = k 2, b 1 ≠ b 2 y = k 2 x+ b 2 k 1 = k 2, b 1 = b 2 k 1 ≠ k 2 k 1 * ถึง 2 = -1 เส้นขนาน เส้นมีความบังเอิญ เส้นตั้งฉาก เส้นตัดกัน
แบบจำลองทางคณิตศาสตร์ที่ฉันสร้างขึ้นจะช่วยให้นักเรียนชั้นประถมศึกษาปีที่ 7 สำรวจฟังก์ชันเชิงเส้นได้อย่างอิสระและเข้าใจฟังก์ชันได้ดีขึ้น

