Otvorena biblioteka - otvorena biblioteka obrazovnih informacija. Izloženo pitagorejsko drvo koje je nanijelo vjetrom Korištenje rekurzivne procedure za konstruiranje figure Pitagorinog drveta

Pitagorino drvo je vrsta fraktala koja se zasniva na figuri poznatoj kao Pitagorine pantalone.

Dokazujući svoju čuvenu teoremu, Pitagora je konstruisao figuru u kojoj su na svakoj strani pravouglog trougla bili kvadrati. S vremenom se ova Pitagorina figura pretvorila u cijelo drvo. Prvi koji je konstruisao Pitagorino drvo tokom Drugog svetskog rata bio je A. Bosman, koristeći običnu crtaću lenjiru.

Jedno od glavnih svojstava Pitagorinog stabla je da kada je površina prvog kvadrata jedan, tada će na svakom nivou zbir površina kvadrata također biti jednak jedan. Klasično Pitagorino stablo ima ugao od 45 stepeni, ali je takođe moguće konstruisati generalizovano Pitagorino stablo koristeći druge uglove. Takvo drvo se naziva Pitagorino drvo koje nosi vjetar. Ako nacrtate samo segmente koji nekako povezuju određene "centre" trouglova, onda ćete dobiti golo pitagorejsko drvo.

Drugi primjer bi bilo poznato "pitagorejsko drvo". Često se prikazuje kao što je prikazano na sl. 3.2. Svaki od pravokutnih trougla u ovom stablu ima unutrašnji ugao od 45°.

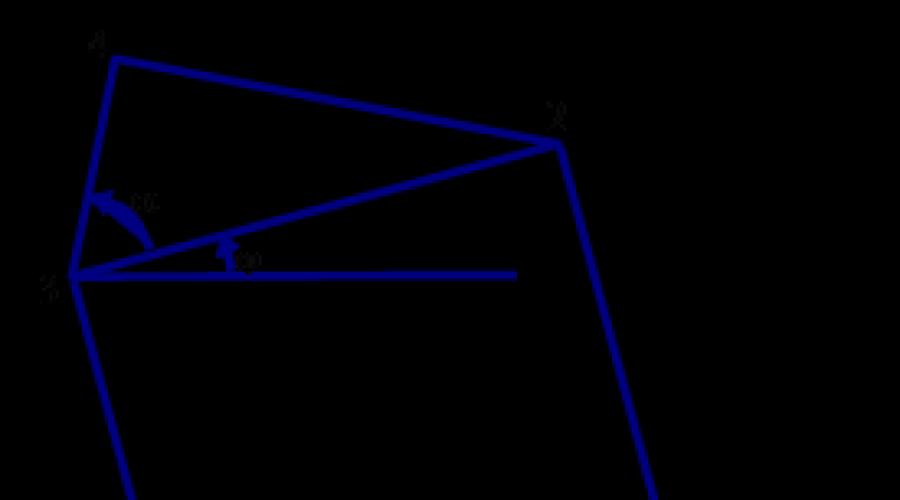
Opet ćemo koristiti generator slučajnih brojeva da kreiramo opštiji program koji može generirati ne samo rižu. 3.2, ali i stvaraju manje pravilna stabla. Uglovi postavljeni na 45° za Sl. 3.2, općenito će biti nasumično postavljen unutar raspona između (45 - delta)° i (45 + delta)° , gdje je vrijednost delta je dat kao ulazni parametar zajedno sa parametrom n, koji određuje dubinu rekurzije. Redovna verzija prikazana na sl. 3.2, dobijeno specificiranjem delta= 0 i n = 7. Na slici je parametar P određuje broj trouglova na putu od korijena do listova drveta. Jezgro programa će biti rekurzivna funkcija square_and_triangle ("kvadrat i trokut") sa parametrom n, koji određuje dubinu rekurzije, kao prvim argumentom. Ako je vrijednost parametra n veća od nule, tada će funkcija square_and_troangle, kao što joj ime govori, nacrtati kvadrat i trokut preko nje, a zatim će se još dva puta pozvati s odgovarajućim novim argumentima, od kojih je prvi postavljeno na n-1. Veličina i položaj kvadrata u potpunosti određuju četiri parametra: X0, Y0, a i j (vidi sliku 3.3). Da biste nacrtali trougao, morate znati ugao a. Ovaj ugao, izražen u stepenima, jednak je 45+devijacija, gde je odstupanje jednako jednom od celih brojeva serije -delta, -delta+I, ... , delta, nasumično odabranih. Na sl. 3.3 potrebne tačke su numerisane uzastopnim brojevima 0,1,2,3,4. Koordinate X0, Y0 tačke O su specificirane u pozivu funkcije. Da bismo izračunali preostale tačke, prvo ćemo razmotriti jednostavniju situaciju sa j = 0, odnosno kada stranica 0 1 kvadrata zauzima horizontalni položaj.

U ovom položaju, koordinate tačaka je vrlo lako odrediti. Oni su pohranjeni u x i y nizovima. Tada se cijela konstrukcija rotira oko tačke O za ugao j. Rezultat rotacije se bilježi u xx i yy nizovima.

/* PYTH_TREE: Varijanta Pitagorinog drveta */

#include "math.h"

#include "stdlib.h"

#include "time.h"

#define pi 3.1415927

#include "stdio.h"

struct (float xx; float yy; int ii;) s;

void pfopen())( fp=fopen("ogrebotina", "wb"); )

void pmove(float x,float y)

( s.xx=x; s.yy=y; s.ii=0; /* 0 = olovka gore */ /* 0 = olovka gore */

fwrite(&s, sizeof s, 1, fp);

void pdraw(float x,float y)

( s.xx=x; s.yy=y; s.ii=1; /* 1 = olovka dolje */ /* 1 = olovka dolje */

fwrite(&s, sizeof s, 1, fp);

void pfclose())( fclose(fp); )

void square_and_troangle(int n,float x0,float y0, float a, float phi)

( float x, y, xx, yy, cphi, sphi, c1, c2, b, c,

alfa, kalfa, salfa;

int i, odstupanje; /* phi i alfa u radijanima */

/* delta u stepenima */

if(n==0) return; /* uglovi phi i alpha u radijanima */

/* ugao delta u stepenima */

devijacija=rand()%(2*delta+1)-delta;

alfa=(45+devijacija)*pi/180,0;

x=x=x0; x=x=x0+a;

y=y=y0; y=y=y0+a;

calpha=cos(alfa); salfa=grijeh(alfa);

c=a*calpha; b=a*salpha;

/* Rotacija oko (x0, y0) kroz ugao phi ; */

/* Rotirajte oko tačke (x0, y0) za ugao phi;*/

cphi=cos(phi); sphi=sin(phi);

c1=x0-x0*cphi+y0*sphi;

c2=y0-x0*sphi-y0*cphi;

za (i=0; i<5; i++)

( xx[i]=x[i]*cphi-y[i]*sphi+c1;

yy[i]=x[i]*sphi+y[i]*cphi+c2;

za (i=0; i<5; i++) pdraw(xx[i],yy[i]);

kvadrat_i_trokut(n-1, xx, yy, c, phi+alpha);

square_and_troangle(n-1, xx, yy, b, phi+alpha-0.5*pi);

pfopen(); vrijeme(&sjeme); srand((int)seed);

printf(" Podesite delta ugao u stepenima (0< delta < 45) ");

scanf("%d", &delta);

printf(" Postavi dubinu rekurzije n "); scanf("%d", &n);

square_and_troangle(n, 0.0, 0.0, 1.0, 0.0);

Ovaj program generiše datoteku SCRATCH koje mora obraditi G program ENPLOT iz predavanja 2. Grafički rezultat programa za delta= 30 i n = 7 je prikazano na sl. 3.4.

Pitagorino drvo je vrsta fraktala koja se zasniva na figuri poznatoj kao Pitagorine pantalone.

Dokazujući svoju čuvenu teoremu, Pitagora je konstruisao figuru u kojoj su na svakoj strani pravouglog trougla bili kvadrati. S vremenom se ova Pitagorina figura pretvorila u cijelo drvo. Prvi koji je konstruisao Pitagorino drvo tokom Drugog svetskog rata bio je A. Bosman, koristeći običnu crtaću lenjiru.

Jedno od glavnih svojstava Pitagorinog stabla je da kada je površina prvog kvadrata jedan, tada će na svakom nivou zbir površina kvadrata također biti jednak jedan. Klasično Pitagorino stablo ima ugao od 45 stepeni, ali je takođe moguće konstruisati generalizovano Pitagorino stablo koristeći druge uglove. Takvo drvo se naziva Pitagorino drvo koje nosi vjetar. Ako nacrtate samo segmente koji nekako povezuju određene "centre" trouglova, onda ćete dobiti golo pitagorejsko drvo.

Mandelbrotov skup je klasičan primjer fraktala... Wikipedia

HTML HTML i HTML5 Dynamic HTML ... Wikipedia

Mandelbrotov skup je klasičan primjer fraktala.Fraktal (lat. fractus crushed) je pojam koji označava geometrijsku figuru koja ima svojstvo samosličnosti, odnosno sastavljena od više dijelova od kojih je svaki sličan cjelini. slika... ... Wikipedia

Fraktal Levyjeve krivulje. Predložio francuski matematičar P. Levy. Ispada ako uzmete pola kvadrata oblika /, a zatim zamijenite svaku stranu istim fragmentom i, ponavljajući ovu operaciju, u ... Wikipediji

Newton Pools ... Wikipedia

Cayley graf je graf koji je konstruisan iz grupe sa istaknutim sistemom generatora. Ime je dobio po Caylee. Definicija Neka su data diskretna grupa G i sistem generatora S. Pretpostavimo da je S = S − 1, odnosno za svaki. Cayley broj grupe G prema sistemu... ... Wikipedia

Graf koji je konstruisan iz grupe sa namenskim sistemom generatora. Ime je dobio po Caylee. Definicija Neka su data diskretna grupa i sistem generatora. Pretpostavimo, odnosno za svaku. Grupa Count Cayley ... Wikipedia

Drevna iranska religija u drevnim izvorima. Članak sadrži pregled podataka antičkih autora (starogrčki, latinski i dijelom jermenski i sirijski) iz 5. stoljeća prije Krista. e. 6. vek nove ere e. o vjeri iranskih naroda iz doba Ahemenida, Parta i moći ... Wikipedia

Kultura naroda koji su ga naseljavali u antičko doba, u 4. 1. milenijumu pr. e., Mesopotamija Mezopotamija Tigris i Eufrat (teritorija modernog Iraka), Sumerani i Akađani, Babilonci i Asirci, koji su stvorili velike države Sumer, Akad, Babilon (vidi... ... Velika sovjetska enciklopedija

Knjige

• Krajem ljeta, Vera Orlovskaya. Nova knjiga Vere Orlovske KRAJ LJETA nastavlja da oduševljava čitaoca svojom raznolikošću oblika i onim što neki od naslova sugerišu: PITAGOROVA FILOZOFIJA U BROJEVIMA, DRVO SNOVA, SIMFONIJA br. 1...
• R-funkcije kao uređaj u primjenama fraktalne geometrije, A. V. Tolok. Matematički aparat teorije R-funkcija koristi se za opisivanje objekata fraktalne geometrije funkcijama ɷ(x) = 0, x ∈ En, pri čemu ɷ(x) ima oblik jednog analitičkog izraza. Od…

Zdravo, prijatelji zainteresovani za fraktale i još mnogo toga. Počevši od ovog trenutka, pokrećem seriju postova u kojima ću objasniti principe konstruisanja najjednostavnijih fraktala. Uvijek je zanimljivo učiti i ja ću vam pomoći u tome: od sada ćemo znati mnogo, mnogo fraktala. Lorenzov atraktor u članku o haosu bio je primjer za to. A danas ću vam pričati o Pitagorinom drvetu.

Pa šta je to? Pitagorino drvo je najjednostavniji fraktal koji se može nacrtati na papiru. Ali zašto se ovaj fraktal zove Pitagorino drvo? Činjenica je da ovdje postoji veza s Pitagorinom teoremom - jednom od temelja euklidske geometrije. Sjećaš li je se? Da vas podsjetim: a2 + b2 = c2 (zbir kvadrata dužina kateta jednak je kvadratu dužine hipotenuze). Ova teorema je poznata još od antičkih vremena, trenutno postoji više od 400 dokaza teoreme, a samo Pitagora ju je prvi geometrijski dokazao. Izgradio je sljedeću figuru: uzeo je pravougli trokut i nacrtao kvadrate na njegovim stranicama. Ova figura se još naziva i "pitagorine pantalone":

Ako nastavimo ovu konstrukciju rekurzivno, na kraju ćemo dobiti Pitagorino stablo:
1. iteracija (u našem Pitagorinom stablu ugao je 45 stepeni):

Druga iteracija:

Treća iteracija:

Deseta iteracija:

Važno svojstvo Pitagorinog stabla: ako je površina prvog kvadrata jednaka jedan, tada će na svakom nivou zbir površina kvadrata također biti jednak jedan.
Ako se ugao promeni od 45 stepeni, onda se mogu konstruisati druge vrste Pitagorinog drveta.
Evo, na primjer, takozvanog „Pitagorinog stabla raznesenog vjetrom“:

Neki generatori fraktalne grafike implementiraju formulu za konstruisanje fraktala na osnovu Pitagorinog stabla. Ova implementacija vrlo podsjeća na IFS sistem, posebno ako kvadrate zamijenite pravokutnicima ili izduženim oblicima.
To je sve za danas, do narednih sastanaka na kojima će biti još mnogo zanimljivih fraktala)