शुद्ध प्रजनन की प्रक्रिया का उपयोग। शुद्ध प्रजनन की प्रक्रिया। प्रजनन और मृत्यु प्रक्रिया
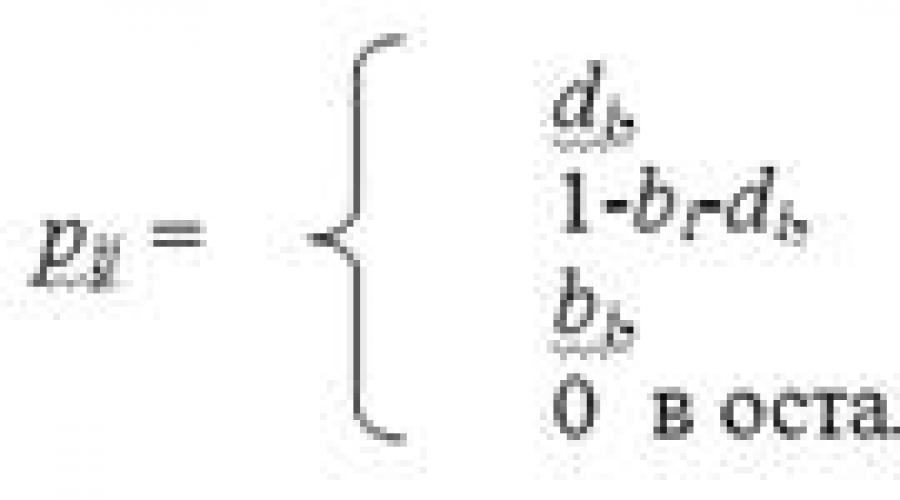
परिचय
इस पेपर में, निरंतर मार्कोव चेन की योजना पर विचार किया जाएगा - तथाकथित "मृत्यु और प्रजनन का आरेख"
प्रजनन और मृत्यु की प्रक्रिया एक अलग या निरंतर समय में बहने वाले राज्यों के एक गणनीय (परिमित या अनंत) सेट के साथ एक यादृच्छिक प्रक्रिया है। यह है कि समय के यादृच्छिक क्षणों में कुछ सिस्टम एक राज्य से दूसरे राज्य से गुजरता है, और कुछ घटनाएं होने पर राज्यों के बीच संक्रमण एक कूद के साथ होती है। एक नियम के रूप में, ये घटनाएं दो प्रकार हैं: उनमें से एक सशर्त रूप से किसी वस्तु का जन्म कहा जाता है, और दूसरा इस वस्तु की मृत्यु है।
यह विषय आर्थिक, पर्यावरणीय और जैविक प्रक्रियाओं के अध्ययन में मार्कोव प्रक्रियाओं के उच्च महत्व के कारण बेहद प्रासंगिक है, इसके अलावा, मार्कोव प्रक्रियाएं जन सेवा के सिद्धांत के केंद्र में हैं, जो वर्तमान में विभिन्न आर्थिक क्षेत्रों में सक्रिय रूप से उपयोग की जाती हैं, उद्यम में प्रक्रियाओं के प्रबंधन सहित।
मौत और प्रजनन की मार्कोव प्रक्रियाओं का व्यापक रूप से भौतिकी, जीवमंडल, पारिस्थितिक तंत्र आदि में होने वाली विभिन्न प्रक्रियाओं को समझाने में उपयोग किया जाता है। यह ध्यान दिया जाना चाहिए कि इस प्रकार की मार्कोव प्रक्रियाओं को जीवविज्ञान में व्यापक रूप से उपयोग के कारण इसका नाम प्राप्त हुआ, विशेष रूप से विभिन्न आबादी के व्यक्तियों के मौत और प्रजनन को मॉडलिंग करते समय।
इस पेपर को कार्य किया जाएगा, जिसका उद्देश्य प्रजनन और मृत्यु की कुछ प्रक्रियाओं के लिए गणितीय अपेक्षाओं को परिभाषित करना है। स्थिर मोड में सिस्टम में आवेदनों की औसत संख्या की गणना के उदाहरण प्रजनन और मृत्यु प्रक्रियाओं के विभिन्न मामलों के लिए किए जाते हैं।
प्रजनन और मृत्यु प्रक्रिया
प्रजनन और मृत्यु की प्रक्रियाएं मार्कोव यादृच्छिक प्रक्रियाओं का एक विशेष मामला है, जो, फिर भी, असतत प्रणालियों के अध्ययन में बहुत व्यापक रूप से उपयोग की जाने वाली स्टोकास्टिक प्रकृति के साथ उपयोग की जाती है। प्रजनन और मृत्यु की प्रक्रिया एक मार्कोव यादृच्छिक प्रक्रिया है जिसमें राज्य ई से संक्रमण केवल ई - 1, ई I और ई + 1 के आसन्न राज्यों में ही अनुमत हैं। जैविक आबादी की मात्रा में होने वाले परिवर्तनों का वर्णन करने के लिए प्रजनन और मृत्यु की प्रक्रिया एक पर्याप्त मॉडल है। इस मॉडल के बाद, ऐसा कहा जाता है कि प्रक्रिया राज्य ई I में है, यदि जनसंख्या की मात्रा सदस्यों के बराबर है। इस मामले में, राज्य ई I से राज्य ई + 1 से संक्रमण जन्म के अनुरूप है, और ई आई -1 में संक्रमण से संक्रमण, मृत्यु, यह माना जाता है कि आबादी की मात्रा अधिक भिन्न नहीं हो सकती है एक; इसका मतलब है कि प्रजनन प्रक्रियाओं और मृत्यु के लिए कई एक साथ जन्म और / या मृत्यु की अनुमति नहीं है।
असतत प्रजनन प्रक्रियाओं और मृत्यु निरंतर की तुलना में कम दिलचस्प हैं, इसलिए भविष्य में उन्हें विस्तार से नहीं माना जाता है और निरंतर प्रक्रियाओं पर केंद्रित होता है। हालांकि, यह ध्यान दिया जाना चाहिए कि लगभग समानांतर गणना अलग-अलग प्रक्रियाओं के लिए गुजरती है। राज्य ई से प्रजनन और मृत्यु की प्रक्रिया का संक्रमण इंटरनेट पर वापस आ गया है ई मैं केवल असतत चेन मार्कोव के लिए तत्काल रुचि का प्रतिनिधित्व करता हूं; निरंतर मामले में, तीव्रता जिसके साथ प्रक्रिया वर्तमान राज्य में लौटती है वह अनंत के बराबर होती है, और इस अनंत को बाहर रखा गया था और इसे निम्नानुसार परिभाषित किया गया है:
राज्यों के बीच संक्रमण की संभावना के एक असतत समय के साथ प्रजनन और मृत्यु की प्रक्रिया के मामले में

यहां डी की संभावना है कि अगले चरण में (जैविक आबादी के संदर्भ में) एक मौत होगी जो आबादी की मात्रा को कम कर देगी इससे पहले कि जनसंख्या की मात्रा इस चरण के बराबर है। इसी प्रकार, बी मैं अगले चरण में जन्म की संभावना है जिससे जनसंख्या की मात्रा में वृद्धि हुई है; यह संभावना है कि इनमें से कोई भी घटना नहीं होगी और अगले चरण में जनसंख्या की मात्रा में बदलाव नहीं आएगा। केवल इन तीन संभावनाओं की अनुमति है। यह स्पष्ट है कि, चूंकि मृत्यु नहीं आ सकती है, अगर किसी प्रकार की मर जाती है।
हालांकि, काउंटरवेट अंतर्ज्ञान में इसकी अनुमति है, जो जन्म की संभावना से मेल खाती है, जब आबादी में एक सदस्य नहीं होता है। हालांकि इसे एक सहज जन्म या दिव्य सृजन के रूप में माना जा सकता है, लेकिन असतत प्रणाली के सिद्धांत में ऐसा मॉडल एक पूरी तरह से सार्थक धारणा है। अर्थात्, मॉडल ऐसा है: जनसंख्या प्रणाली में दावों का प्रवाह है, मृत्यु का अर्थ है सिस्टम की आवश्यकता की देखभाल, और जन्म प्रणाली की नई मांग से मेल खाता है। यह स्पष्ट है कि ऐसे मॉडल में मुफ्त सिस्टम में एक नई आवश्यकता (जन्म) दर्ज करना काफी संभव है। प्रजनन और मृत्यु की सामान्य प्रक्रिया के लिए संक्रमण के संभाव्यता मैट्रिक्स में निम्नलिखित रूप हैं:

यदि मार्कोव श्रृंखला अंतिम है, तो मैट्रिक्स की बाद वाली रेखा फॉर्म में लिखी गई है; यह इस तथ्य से मेल खाती है कि जनसंख्या अधिकतम मात्रा एन तक पहुंचने के बाद कोई प्रजनन की अनुमति नहीं है। मैट्रिक्स टी में केवल मुख्य विकर्ण और इसके निकटतम दो विकर्णों पर शून्य सदस्य होते हैं। इस तरह के एक विशेष प्रकार के मैट्रिक्स टी की वजह से, यह उम्मीद करना स्वाभाविक है कि प्रजनन और मृत्यु की प्रक्रिया का विश्लेषण कठिनाइयों का कारण नहीं बनना चाहिए। इसके बाद, हम केवल प्रजनन और मृत्यु की निरंतर प्रक्रियाओं पर विचार करेंगे, जिसमें राज्य ई से संक्रमण केवल पड़ोसी राज्यों ई -1 (मृत्यु) और ई I + 1 (जन्म) में ही संभव है। प्रजनन की तीव्रता से निंदा; यह उस गति का वर्णन करता है जिसके साथ मेरी मात्रा में प्रजनन होता है। इसी प्रकार, मैं के माध्यम से, हम मृत्यु की तीव्रता को दर्शाते हैं, निर्दिष्ट गति की गति की मात्रा में मृत्यु उत्पन्न होती है। ध्यान दें कि पेश की गई प्रजनन तीव्रता और मृत्यु उस समय पर निर्भर नहीं है, और राज्य ई पर निर्भर करती है, इसलिए, हम मार्कोव प्रकार की प्रजनन और मृत्यु की एक सतत सजातीय श्रृंखला प्राप्त करते हैं। ये विशेष पदनाम पेश किए जाते हैं क्योंकि वे सीधे असतत प्रणालियों के सिद्धांत में अपनाए गए नोटेशन का नेतृत्व करते हैं। पहले दर्ज किए गए पदों के आधार पर, हमारे पास है:
i \u003d q i, i + 1 और i \u003d q i, i-1।
निकटतम आसन्न राज्यों में केवल स्वीकार्य संक्रमण की आवश्यकता का मतलब है कि इस तथ्य के आधार पर कि
हम q ii \u003d - (i + i) प्राप्त करते हैं। इस प्रकार, प्रजनन और मृत्यु की सामान्य सजातीय प्रक्रिया के संक्रमण की तीव्रता के मैट्रिक्स फॉर्म लेते हैं:

ध्यान दें कि मुख्य विकर्ण और उसके पड़ोसी के अपवाद और ऊपर से, मैट्रिक्स के सभी तत्व शून्य हैं। संक्रमण तीव्रता के संबंधित ग्राफ संबंधित आकृति (2.1) में प्रस्तुत किए जाते हैं:
चित्रा 2.1 - प्रजनन और मृत्यु की प्रक्रिया के लिए संक्रमण तीव्रता की गिनती
प्रजनन और मृत्यु की निरंतर प्रक्रिया का एक और सटीक निर्धारण निम्नानुसार है: कुछ प्रक्रिया प्रजनन और मृत्यु की प्रक्रिया है, अगर यह कई राज्यों के साथ मार्कोव की एक सजातीय श्रृंखला है (ई 0, ई 1, ई 2, ... ), यदि जन्म और मृत्यु स्वतंत्र घटनाएं हैं (यह सीधे मार्कोव संपत्ति से लेकर) है और यदि निम्न स्थितियां संतुष्ट हैं:
(समय अंतराल (टी, टी + डीटी) में बिल्कुल 1 जन्म, जनसंख्या की मात्रा I के बराबर है);
(समय अंतराल में 1 मौत (टी, टी + डीटी) | जनसंख्या की मात्रा I के बराबर है);
\u003d (समय अंतराल (टी, टी + डीटी) में बिल्कुल 0 जन्म | आबादी की मात्रा I के बराबर है);
\u003d (समय अंतराल में 0 मौतें (टी, टी + डीटी) | आबादी की मात्रा I के बराबर है)।
इस प्रकार, ए टी सटीकता एन व्यक्तियों की आबादी में एक नए व्यक्ति के जन्म की संभावना है, ए - उस समय के दौरान इस आबादी में व्यक्तियों की मौत की संभावना।
संक्रमण की संभावनाएं कोल्मोगोरोव के विपरीत समीकरणों को संतुष्ट करती हैं। इस प्रकार, संभावना है कि समय पर पुनरुत्पादन और मृत्यु की निरंतर प्रक्रिया राज्य ई (I के बराबर आबादी की मात्रा) में है (2.1) में निर्धारित है:

गैर-अस्थिर मामले में अंतर समीकरणों की प्राप्त प्रणाली को हल करने के लिए, जब संभावनाएं पीआई (टी), i \u003d 0,1,2, ..., उस समय पर निर्भर करती हैं, प्रारंभिक संभावनाओं के वितरण को निर्दिष्ट करना आवश्यक है। (0), i \u003d 0,1,2, ..., टी \u003d 0 पर। इसके अलावा, सामान्यीकरण की स्थिति संतुष्ट होनी चाहिए।
अब हम शुद्ध प्रजनन की सबसे सरल प्रक्रिया पर विचार करते हैं, जिसे एक प्रक्रिया के रूप में परिभाषित किया जाता है जिसके लिए मैं सभी के लिए i \u003d 0 करता हूं। इसके अलावा, समस्या के बड़े सरलीकरण के लिए, मान लीजिए कि मैं \u003d सभी के लिए \u003d 0,1,2, .... समीकरण में इन मानों को प्रतिस्थापित करना (2.1) हम प्राप्त करते हैं (2.2):

सादगी के लिए, हम यह भी मानते हैं कि प्रक्रिया शून्य सदस्यों पर शून्य पल में शुरू होती है, यह है:
यहां से पी 0 (टी) के लिए हमें एक समाधान मिलता है:
I \u003d 1 पर समीकरण (2.2) के लिए इस समाधान को प्रतिस्थापित करना, हम समीकरण पर पहुंचते हैं:
इस अंतर समीकरण का समाधान स्पष्ट रूप से फॉर्म है:
यह पोइसन का परिचित वितरण है। इस प्रकार, निरंतर तीव्रता के साथ शुद्ध प्रजनन की प्रक्रिया poisson प्रवाह बनाने के जन्म के अनुक्रम की ओर ले जाती है।
व्यावहारिक शर्तों में सबसे बड़ी रुचि स्थिर मोड में प्रजनन प्रक्रिया और मृत्यु के राज्यों की संभावनाओं का प्रतिनिधित्व करती है। इस प्रक्रिया में एक एर्गोडिक संपत्ति है, यानी, सीमाएं हैं
हम सीमा की संभावनाओं की परिभाषा को बदलते हैं p i। स्थिर शासन की संभावनाओं को निर्धारित करने के लिए समीकरण सीधे (2.1) से प्राप्त किए जा सकते हैं, दिए गए डीपी I (टी) / डीटी \u003d 0 के साथ:
सामान्यीकरण की स्थिति (2.4) के संबंध में समीकरणों की परिणामी प्रणाली हल की जाती है:
प्रजनन और मृत्यु की प्रक्रिया के स्थापित मोड के लिए समीकरण (2.3) की प्रणाली को चित्रा 2.1 में संक्रमण की तीव्रता के ग्राफ द्वारा सीधे किया जा सकता है, प्रक्रिया की एक अलग स्थिति में संभाव्यता धाराओं की समानता के सिद्धांत को लागू किया जा सकता है। उदाहरण के लिए, यदि आप स्थिर मोड में ई I की स्थिति पर विचार करते हैं, तो:
प्रायिकता की तीव्रता में और
संभावना प्रवाह की तीव्रता से।
संतुलन स्थिति में, ये दो धाराएं बराबर होनी चाहिए, और इसलिए हम सीधे प्राप्त करते हैं:
लेकिन यह सिस्टम (2.3) में बिल्कुल पहली समानता है। इसी तरह, आप सिस्टम की दूसरी समानता प्राप्त कर सकते हैं। प्रवाह के संरक्षण पर वही तर्क, जिसे पहले दिखाया गया था, किसी भी बंद सीमा के माध्यम से संभावनाओं की धारा पर लागू किया जा सकता है। उदाहरण के लिए, प्रत्येक राज्य को हाइलाइट करने और इसके लिए एक समीकरण बनाने के बजाय, आप समोच्चों के अनुक्रम का चयन कर सकते हैं, जिनमें से पहला राज्य ई 0 को कवर करता है, दूसरा राज्य ई 0 और ई 1 है, और इतने पर भी शामिल है नई सीमा में हर बार अगला राज्य। फिर आई-वें समोच्च (आसपास के राज्य ई 0, ई 1, ..., ई आई -1) के लिए, संभाव्यता प्रवाह का संरक्षण निम्नलिखित सरल रूप में लिखा जा सकता है:
समानता (2.5) को एक नियम के रूप में तैयार किया जा सकता है: रोगीकरण मोड में प्रजनन और मृत्यु की सबसे सरल प्रणाली के लिए, किसी भी दो आसन्न राज्यों के बीच संभाव्यता धाराएं बराबर होती हैं।
समीकरणों की परिणामी प्रणाली कम पहले के बराबर है। समीकरणों की अंतिम प्रणाली को संकलित करने के लिए, पड़ोसी राज्यों को अलग करने वाली ऊर्ध्वाधर रेखा को ले जाना आवश्यक है, और परिणामी सीमा के माध्यम से धाराओं को समान रखें।
गणितीय प्रेरण द्वारा सिस्टम (2.5) का समाधान पाया जा सकता है।
I \u003d 1 में हमारे पास है
प्राप्त समानता के प्रकार से पता चलता है कि समीकरणों की प्रणाली का समग्र समाधान (2.5) का रूप है:
या, यह देखते हुए, परिभाषा के अनुसार, एक खाली सेट पर काम एक है:
इस प्रकार, स्थिर मोड के लिए सभी संभावनाएं पी मैं केवल अज्ञात निरंतर पी 0 के माध्यम से व्यक्त की जाती हैं। समानता (2.4) पी 0 निर्धारित करने के लिए एक अतिरिक्त शर्त देता है। फिर, सभी I पर संक्षेप में, पी 0 के लिए हमें मिलता है (2.7):

आइए हम स्थिर संभावनाओं के अस्तित्व के मुद्दे पर जाएं। अभिव्यक्तियों को निर्दिष्ट करने के लिए, आवश्यकता आमतौर पर अतिरंजित होती है ताकि पी 0\u003e 0 हो। यह स्पष्ट रूप से संबंधित समीकरणों में प्रजनन गुणांक और मृत्यु पर प्रतिबंध लगा देता है। अनिवार्य रूप से यह आवश्यक है कि सिस्टम कभी-कभी खाली होता है; यदि आप वास्तविक जीवन के उदाहरणों को चालू करते हैं तो यह स्थिरता की स्थिति बहुत उचित प्रतीत होती है। यदि यह बहुत तेजी से बढ़ता है, तो यह तब हो सकता है कि अंत बिंदु पर सकारात्मक संभावना के साथ, प्रक्रिया "एक असीमित रिमोट पॉइंट" में चरण स्थान (0.1, ...) छोड़ देगी? (जनसंख्या में व्यक्ति बहुत अधिक होंगे)। दूसरे शब्दों में, प्रक्रिया नियमित नहीं होगी, और फिर समानता (2.4) टूट जाएगी। हम निम्नलिखित दो राशियों को परिभाषित करते हैं:

प्रजनन और मृत्यु की प्रक्रिया की नियमितता के लिए, यह आवश्यक है और एस 2 \u003d के लिए पर्याप्त है।
अपने स्थिर वितरण के अस्तित्व के लिए, यह आवश्यक है और एस 1 के लिए पर्याप्त है< .
प्रश्न में कार्यवाही प्रक्रिया के ई I के सभी राज्यों के क्रम में और मौतें एर्गोडिक थीं, और श्रृंखला एस के पर्याप्त अभिसरण थे< , при этом ряд должен расходиться S 2 = . Только эргодический случай приводит к установившимся вероятностям P i , i = 0, 1, 2, …, и именно этот случай представляет интерес. Заметим, что условия эргодичности выполняются, например, когда, начиная с некоторого i, все члены последовательности {} ограничены единицей, т. е. тогда, когда существует некоторое i 0 (и некоторое С<1) такое, что для всех ii 0 выполняется неравенство:
इस असमानता को एक साधारण व्याख्या दी जा सकती है: कुछ राज्य ई I और सभी बाद के राज्यों से शुरू, प्रजनन की धारा की तीव्रता मृत्यु के प्रवाह की तीव्रता से कम होनी चाहिए।
कभी-कभी अभ्यास में "शुद्ध" प्रजनन की प्रक्रियाएं होती हैं। "शुद्ध" प्रजनन की प्रक्रिया मृत्यु और प्रजनन की प्रक्रिया है, जिसमें सभी मौत की प्रवाह शून्य शून्य होती है। राज्यों की संख्या को सीमित किए बिना ऐसी प्रक्रिया के राज्यों का ग्राफ आंकड़ा (2.2) में दिखाया गया है:

चित्रा 2.2 - "शुद्ध" प्रजनन की प्रक्रिया के लिए संक्रमण तीव्रता का ग्राफ
इसी प्रकार, "स्वच्छ" मौत की अवधारणा पेश की गई है। "स्वच्छ" मौत की प्रक्रिया को मौत और प्रजनन की इस तरह की प्रक्रिया कहा जाता है, जिसमें सभी प्रजनन प्रवाह की तीव्रता शून्य होती है। राज्यों की संख्या को सीमित किए बिना ऐसी प्रक्रिया के राज्यों का ग्राफ आंकड़ा में दिखाया गया है:

चित्रा 2.3 - "शुद्ध" मौत की प्रक्रिया के लिए संक्रमण तीव्रता की गिनती
ऐसी प्रक्रियाओं के लिए कोल्मोगोरोव समीकरण प्रणाली समीकरणों की प्रणाली (2.1) से प्राप्त की जा सकती है, जिसमें प्रवाह प्रक्रिया की सभी तीव्रताओं को शून्य के बराबर प्रवाह करना आवश्यक है :.
पोइसन प्रक्रिया का सबसे सरल सामान्यीकरण इस धारणा के तहत प्राप्त किया जाता है कि कूद की संभावनाएं सिस्टम की वर्तमान स्थिति पर निर्भर हो सकती हैं। इससे हमें निम्नलिखित आवश्यकताओं की ओर ले जाता है।
Postulates। (i) राज्य से प्रत्यक्ष संक्रमण केवल राज्य के लिए संभव है। (ii) यदि समय के समय प्रणाली एक राज्य में है, तो (सशर्त) बाद के कम समय के अंतराल में एक कूद की संभावना और है फिर (सशर्त) इस अंतराल में एक से अधिक कूद की संभावना है।
इस धारणा की एक विशिष्ट विशेषता यह है कि जिस समय प्रणाली किसी भी विशेष राज्य में खर्च करती है वह कोई भूमिका नहीं निभाती है; अचानक राज्य परिवर्तन संभव हैं, हालांकि, सिस्टम एक राज्य में है, यह उम्र नहीं है।
यह संभावना है कि समय के समय सिस्टम एक राज्य में है। ये कार्य अलग-अलग समीकरणों की प्रणाली को संतुष्ट करते हैं, जिन्हें पिछले पैराग्राफ के कारणों का उपयोग करके प्राप्त किया जा सकता है (5) पिछले पैराग्राफ में प्रतिस्थापित किया गया है
इस प्रकार, हम अंतर समीकरणों की मुख्य प्रणाली प्राप्त करते हैं
 (2)
(2)
पोइसन प्रक्रिया में, यह समझना स्वाभाविक था कि समय के समय, सिस्टम प्रारंभिक स्थिति से बाहर आता है। अब हम एक सामान्य मामले को स्वीकार कर सकते हैं जब प्रणाली मनमानी प्रारंभिक स्थिति से बाहर आती है। फिर हमें वह मिलता है
ये प्रारंभिक स्थितियां एकल प्रणाली (2) के समाधान को परिभाषित करती हैं। (विशेष रूप से, )। कई लेखकों द्वारा स्वतंत्र रूप से प्रदर्शित होने के लिए स्पष्ट सूत्र, लेकिन हमारे लिए वे रुचि का प्रतिनिधित्व नहीं करते हैं।
उदाहरण। रेडियोधर्मी क्षय। कणों के उत्सर्जन के परिणामस्वरूप या त्रिज्या, एक रेडियोधर्मी परमाणु, यूरेनियम कहते हैं, किसी अन्य प्रजाति के परमाणु में बदल सकते हैं। प्रत्येक दृश्य एक संभावित स्थिति है, और जब प्रक्रिया आगे बढ़ती है, तो हमें संक्रमण का अनुक्रम मिलता है। अपनाए गए भौतिक सिद्धांतों के अनुसार, संक्रमण की संभावना तब तक अपरिवर्तित बनी हुई है जब तक कि परमाणु राज्य में न हो, और इस परिकल्पना को हमारी प्रारंभिक धारणा में अभिव्यक्ति मिलती है। इसलिए, इस प्रक्रिया को विभेदक समीकरणों (2) (तथ्य, प्रसिद्ध भौतिक विज्ञानी) द्वारा वर्णित किया गया है। यदि - अंतिम राज्य, जिसमें से कोई अन्य संक्रमण असंभव नहीं है, फिर सिस्टम (2) टूटा हुआ है। (जब हम स्वचालित रूप से प्राप्त करते हैं)।
बेलारूस गणराज्य की शिक्षा मंत्रालय
शिक्षा की स्थापना
"गोमेल स्टेट यूनिवर्सिटी
फ्रांसिस स्कोराइना के नाम पर
गणितीय संकाय
आर्थिक साइबरनेटिक्स और संभाव्यता सिद्धांत विभाग
कोर्स परियोजना
प्रजनन और मृत्यु प्रक्रियाओं की स्थिर विशेषताएं
निष्पादक:
बुखोवेट विक्टोरिया
एलेक्ज़ेंड्रोव्ना
वैज्ञानिक सलाहकार:
विभागाध्यक्ष,
Malinkovsky Yuri।
Vladimirovich
गोमेल 2011।
परिचय
प्रजनन और मृत्यु प्रक्रिया
सरल द्रव्यमान रखरखाव प्रणाली के मामले में प्रजनन और मृत्यु प्रक्रियाओं के उदाहरण
मास रखरखाव प्रणाली एम / एम / एन के लिए गणितीय अपेक्षा की 3 परिभाषा
मास रखरखाव प्रणाली एम / एम / एन / एन के लिए गणितीय अपेक्षा की 4 परिभाषा
प्रजनन और मृत्यु की कुछ प्रक्रियाओं के लिए गणितीय उम्मीद की परिभाषा
रैखिक रूप से बढ़ती जन्म तीव्रता और चतुर्भुज बढ़ती मौत की तीव्रता के साथ प्रजनन और मृत्यु की प्रक्रिया
4 अतिरिक्त प्रवाह और उपकरणों की अनंत संख्या
आवेदन के रहने के समय के लिए प्रतिबंध के साथ 5 प्रणाली
आवेदन रहने के समय के लिए प्रतिबंध के साथ 6 प्रणाली, अतिरिक्त धारा और उपकरणों की अनंत संख्या
निष्कर्ष
बड़े पैमाने पर रखरखाव गणितीय उम्मीद
परिचय
इस पेपर में, निरंतर मार्कोव चेन की योजना पर विचार किया जाएगा - तथाकथित "मृत्यु और प्रजनन का आरेख"
प्रजनन और मृत्यु की प्रक्रिया एक अलग या निरंतर समय में बहने वाले राज्यों के एक गणनीय (परिमित या अनंत) सेट के साथ एक यादृच्छिक प्रक्रिया है। यह है कि समय के यादृच्छिक क्षणों में कुछ सिस्टम एक राज्य से दूसरे राज्य से गुजरता है, और कुछ घटनाएं होने पर राज्यों के बीच संक्रमण एक कूद के साथ होती है। एक नियम के रूप में, ये घटनाएं दो प्रकार हैं: उनमें से एक सशर्त रूप से किसी वस्तु का जन्म कहा जाता है, और दूसरा इस वस्तु की मृत्यु है।
यह विषय आर्थिक, पर्यावरणीय और जैविक प्रक्रियाओं के अध्ययन में मार्कोव प्रक्रियाओं के उच्च महत्व के कारण बेहद प्रासंगिक है, इसके अलावा, मार्कोव प्रक्रियाएं जन सेवा के सिद्धांत के केंद्र में हैं, जो वर्तमान में विभिन्न आर्थिक क्षेत्रों में सक्रिय रूप से उपयोग की जाती हैं, उद्यम में प्रक्रियाओं के प्रबंधन सहित।
मौत और प्रजनन की मार्कोव प्रक्रियाओं का व्यापक रूप से भौतिकी, जीवमंडल, पारिस्थितिक तंत्र आदि में होने वाली विभिन्न प्रक्रियाओं को समझाने में उपयोग किया जाता है। यह ध्यान दिया जाना चाहिए कि इस प्रकार की मार्कोव प्रक्रियाओं को जीवविज्ञान में व्यापक रूप से उपयोग के कारण इसका नाम प्राप्त हुआ, विशेष रूप से विभिन्न आबादी के व्यक्तियों के मौत और प्रजनन को मॉडलिंग करते समय।
इस पेपर को कार्य किया जाएगा, जिसका उद्देश्य प्रजनन और मृत्यु की कुछ प्रक्रियाओं के लिए गणितीय अपेक्षाओं को परिभाषित करना है। स्थिर मोड में सिस्टम में आवेदनों की औसत संख्या की गणना के उदाहरण प्रजनन और मृत्यु प्रक्रियाओं के विभिन्न मामलों के लिए किए जाते हैं।
1. प्रजनन और मृत्यु की प्रक्रिया
प्रजनन और मृत्यु की प्रक्रियाएं मार्कोव यादृच्छिक प्रक्रियाओं का एक विशेष मामला है, जो, फिर भी, असतत प्रणालियों के अध्ययन में बहुत व्यापक रूप से उपयोग की जाने वाली स्टोकास्टिक प्रकृति के साथ उपयोग की जाती है। प्रजनन और मृत्यु की प्रक्रिया एक मार्कोव यादृच्छिक प्रक्रिया है जिसमें राज्य ई से संक्रमण होता है मैं। केवल पड़ोसी राज्यों में अनुमति दी i-1। इ। मैं। और ई। i + 1। । जैविक आबादी की मात्रा में होने वाले परिवर्तनों का वर्णन करने के लिए प्रजनन और मृत्यु की प्रक्रिया एक पर्याप्त मॉडल है। इस मॉडल के बाद, वे कहते हैं कि प्रक्रिया एक राज्य ई में है मैं। यदि जनसंख्या की मात्रा सदस्यों के बराबर है। इस मामले में, राज्य ई से संक्रमण मैं। राज्य ई। i + 1। जन्म के अनुरूप, और ई से संक्रमण मैं। ई में i-1। - मौत, यह माना जाता है कि आबादी की मात्रा एक से अधिक नहीं भिन्न हो सकती है; इसका मतलब है कि प्रजनन प्रक्रियाओं और मृत्यु के लिए कई एक साथ जन्म और / या मृत्यु की अनुमति नहीं है।
असतत प्रजनन प्रक्रियाओं और मृत्यु निरंतर की तुलना में कम दिलचस्प हैं, इसलिए भविष्य में उन्हें विस्तार से नहीं माना जाता है और निरंतर प्रक्रियाओं पर केंद्रित होता है। हालांकि, यह ध्यान दिया जाना चाहिए कि लगभग समानांतर गणना अलग-अलग प्रक्रियाओं के लिए गुजरती है। राज्य ई से प्रजनन और मृत्यु की संक्रमण प्रक्रिया मैं। वापस राज्य ई मैं। केवल असतत चेन मार्कोव के लिए प्रत्यक्ष ब्याज का प्रतिनिधित्व करता है; निरंतर मामले में, तीव्रता जिसके साथ प्रक्रिया वर्तमान राज्य में लौटती है वह अनंत के बराबर होती है, और इस अनंत को बाहर रखा गया था और इसे निम्नानुसार परिभाषित किया गया है:
राज्यों के बीच संक्रमण की संभावना के एक असतत समय के साथ प्रजनन और मृत्यु की प्रक्रिया के मामले में
यहां, डी संभावना है कि अगले चरण में (जैविक आबादी के संदर्भ में) एक मौत होगी जो आबादी की मात्रा को कम कर देगी इससे पहले कि जनसंख्या की मात्रा इस चरण के बराबर है। इसी तरह, द्वि अगले चरण में जन्म की संभावना है, जिससे जनसंख्या की मात्रा में वृद्धि हुई है; यह संभावना है कि इनमें से कोई भी घटना नहीं होगी और अगले चरण में जनसंख्या की मात्रा में बदलाव नहीं आएगा। केवल इन तीन संभावनाओं की अनुमति है। यह स्पष्ट है कि, चूंकि मृत्यु नहीं आ सकती है, अगर किसी प्रकार की मर जाती है।
हालांकि, काउंटरवेट अंतर्ज्ञान में इसकी अनुमति है, जो जन्म की संभावना से मेल खाती है, जब आबादी में एक सदस्य नहीं होता है। हालांकि इसे एक सहज जन्म या दिव्य सृजन के रूप में माना जा सकता है, लेकिन असतत प्रणाली के सिद्धांत में ऐसा मॉडल एक पूरी तरह से सार्थक धारणा है। अर्थात्, मॉडल ऐसा है: जनसंख्या प्रणाली में दावों का प्रवाह है, मृत्यु का अर्थ है सिस्टम की आवश्यकता की देखभाल, और जन्म प्रणाली की नई मांग से मेल खाता है। यह स्पष्ट है कि ऐसे मॉडल में मुफ्त सिस्टम में एक नई आवश्यकता (जन्म) दर्ज करना काफी संभव है। प्रजनन और मृत्यु की सामान्य प्रक्रिया के लिए संक्रमण के संभाव्यता मैट्रिक्स में निम्नलिखित रूप हैं:
यदि मार्कोव श्रृंखला अंतिम है, तो मैट्रिक्स की बाद वाली रेखा फॉर्म में लिखी गई है; यह इस तथ्य से मेल खाती है कि जनसंख्या अधिकतम मात्रा एन तक पहुंचने के बाद कोई प्रजनन की अनुमति नहीं है। मैट्रिक्स टी में केवल मुख्य विकर्ण और इसके निकटतम दो विकर्णों पर शून्य सदस्य होते हैं। इस तरह के एक विशेष प्रकार के मैट्रिक्स टी की वजह से, यह उम्मीद करना स्वाभाविक है कि प्रजनन और मृत्यु की प्रक्रिया का विश्लेषण कठिनाइयों का कारण नहीं बनना चाहिए। इसके बाद, हम केवल प्रजनन और मृत्यु की निरंतर प्रक्रियाओं पर विचार करेंगे, जिसमें ईआई राज्य से संक्रमण केवल ईआई -1 (मौत) और ईआई + 1 (जन्म) के पड़ोसी राज्यों में संभव है। पुनरुत्पादन की तीव्रता ली द्वारा निरूपित; यह उस गति का वर्णन करता है जिसके साथ मेरी मात्रा में प्रजनन होता है। इसी प्रकार, एमआई के माध्यम से, हम मृत्यु की तीव्रता को दर्शाते हैं, निर्दिष्ट गति के साथ गति की मात्रा में मृत्यु उत्पन्न होती है। ध्यान दें कि पेश की गई प्रजनन तीव्रता और मृत्यु उस समय पर निर्भर नहीं है, और राज्य ईई पर निर्भर करती है, इसलिए, हम मार्कोव प्रकार की प्रजनन और मृत्यु की एक सतत सजातीय श्रृंखला प्राप्त करते हैं। ये विशेष पदनाम पेश किए जाते हैं क्योंकि वे सीधे असतत प्रणालियों के सिद्धांत में अपनाए गए नोटेशन का नेतृत्व करते हैं। पहले दर्ज किए गए पदों के आधार पर, हमारे पास है:
ली \u003d क्यूई, मैं + 1 और एमआई \u003d क्यूई, आई -1।
निकटतम आसन्न राज्यों में केवल स्वीकार्य संक्रमण की आवश्यकता का मतलब है कि इस तथ्य के आधार पर कि
हम qii \u003d - (mi + li) प्राप्त करते हैं। इस प्रकार, प्रजनन और मृत्यु की सामान्य सजातीय प्रक्रिया के संक्रमण की तीव्रता के मैट्रिक्स फॉर्म लेते हैं:
ध्यान दें कि मुख्य विकर्ण और उसके पड़ोसी के अपवाद और ऊपर से, मैट्रिक्स के सभी तत्व शून्य हैं। संक्रमण तीव्रता के संबंधित ग्राफ संबंधित आकृति (2.1) में प्रस्तुत किए जाते हैं:
चित्रा 2.1 - प्रजनन और मृत्यु की प्रक्रिया के लिए संक्रमण तीव्रता की गिनती
प्रजनन और मृत्यु की निरंतर प्रक्रिया का एक और सटीक निर्धारण निम्नानुसार है: कुछ प्रक्रिया प्रजनन और मृत्यु की प्रक्रिया है, यदि यह एकाधिक राज्यों (ई 0, ई 1, ई 2, ...) के साथ एक सजातीय मार्कोव श्रृंखला है, तो यदि जन्म और मृत्यु स्वतंत्र घटनाएं होती हैं (यह सीधे मार्कोव संपत्ति से होती है) और यदि निम्न स्थितियां संतुष्ट हैं:
1) (समय अंतराल (टी, टी +? टी) में बिल्कुल 1 जन्म, जनसंख्या मात्रा I के बराबर है);
2) (समय अंतराल में 1 मौत (टी, टी +? टी) | जनसंख्या की मात्रा I के बराबर है);
3) \u003d (समय अंतराल में 0 जन्म (टी, टी +? टी) | आबादी की मात्रा I के बराबर है);
4) \u003d (समय अंतराल में 0 मौतें (टी, टी +? टी) | आबादी की मात्रा I के बराबर है)।
इस प्रकार, ए टी सटीकता एन व्यक्तियों की आबादी में एक नए व्यक्ति के जन्म की संभावना है, ए - उस समय के दौरान इस आबादी में व्यक्तियों की मौत की संभावना।
संक्रमण की संभावनाएं कोल्मोगोरोव के विपरीत समीकरणों को संतुष्ट करती हैं। इस प्रकार, संभावना है कि समय पर पुनरुत्पादन और मृत्यु की निरंतर प्रक्रिया राज्य ईआई में है (जनसंख्या की मात्रा आई के बराबर है) फॉर्म में निर्धारित की जाती है (2.1):
गैर-अस्थिर मामले में अंतर समीकरणों की परिणामी प्रणाली को हल करने के लिए, जब संभावनाएं पीआई (टी), i \u003d 0,1,2, ..., उस समय पर निर्भर करती हैं, प्रारंभिक संभावनाओं के वितरण को सेट करना आवश्यक है (0), i \u003d 0,1,2, ..., टी \u003d 0 पर। इसके अलावा, सामान्यीकरण की स्थिति संतुष्ट होनी चाहिए।
अब शुद्ध प्रजनन की सबसे सरल प्रक्रिया पर विचार करें, जिसे एक प्रक्रिया के रूप में परिभाषित किया गया है जिसके लिए Mi \u003d 0 सभी के लिए। इसके अलावा, समस्या के बड़े सरलीकरण के लिए, मान लीजिए कि ली \u003d एल सभी के लिए i \u003d 0,1,2, .... समीकरण में इन मानों को प्रतिस्थापित करना (2.1) हम प्राप्त करते हैं (2.2):
सादगी के लिए, हम यह भी मानते हैं कि प्रक्रिया शून्य सदस्यों पर शून्य पल में शुरू होती है, यह है:
इसलिए पी 0 (टी) के लिए हमें एक समाधान मिलता है:
I \u003d 1 पर समीकरण (2.2) के लिए इस समाधान को प्रतिस्थापित करना, हम समीकरण पर पहुंचते हैं:
इस अंतर समीकरण का समाधान स्पष्ट रूप से फॉर्म है:
यह पोइसन का परिचित वितरण है। इस प्रकार, निरंतर तीव्रता के साथ शुद्ध प्रजनन की प्रक्रिया एल पोइसन प्रवाह बनाने वाले जन्मों के अनुक्रम की ओर ले जाती है।
व्यावहारिक शर्तों में सबसे बड़ी रुचि स्थिर मोड में प्रजनन प्रक्रिया और मृत्यु के राज्यों की संभावनाओं का प्रतिनिधित्व करती है। इस प्रक्रिया में एक एर्गोडिक संपत्ति है, यानी, सीमाएं हैं
आइए पीआई की सीमा संभावनाओं की परिभाषा की ओर मुड़ें। स्थिर मोड की संभावनाओं को निर्धारित करने के लिए समीकरण सीधे (2.1) से प्राप्त किए जा सकते हैं, दिए गए कि डीपीआई (टी) / डीटी \u003d 0 के साथ:
सामान्यीकरण की स्थिति (2.4) के संबंध में समीकरणों की परिणामी प्रणाली हल की जाती है:
प्रजनन और मृत्यु की प्रक्रिया के स्थापित मोड के लिए समीकरण (2.3) की प्रणाली को चित्रा 2.1 में संक्रमण की तीव्रता के ग्राफ द्वारा सीधे किया जा सकता है, प्रक्रिया की एक अलग स्थिति में संभाव्यता धाराओं की समानता के सिद्धांत को लागू किया जा सकता है। उदाहरण के लिए, यदि आप स्थिर मोड में ईआई स्थिति पर विचार करते हैं, तो:
प्रायिकता की तीव्रता में और
संभावना प्रवाह की तीव्रता से।
संतुलन स्थिति में, ये दो धाराएं बराबर होनी चाहिए, और इसलिए हम सीधे प्राप्त करते हैं:
लेकिन यह सिस्टम (2.3) में बिल्कुल पहली समानता है। इसी तरह, आप सिस्टम की दूसरी समानता प्राप्त कर सकते हैं। प्रवाह के संरक्षण पर वही तर्क, जिसे पहले दिखाया गया था, किसी भी बंद सीमा के माध्यम से संभावनाओं की धारा पर लागू किया जा सकता है। उदाहरण के लिए, प्रत्येक राज्य को अलग करने और इसके लिए एक समीकरण करने के बजाय, आप समोच्चों के अनुक्रम का चयन कर सकते हैं, जिनमें से पहला राज्य ई 0, दूसरा राज्य ई 0 और ई 1, और इसी तरह, प्रत्येक बार अगले राज्य को शामिल करता है एक और राज्य। फिर आई-वें समोच्च (आसपास के राज्य ई 0, ई 1, ..., ईआई -1) के लिए, संभाव्यता धारा निम्नलिखित सरल रूप में लिखी जा सकती है:
समानता (2.5) को एक नियम के रूप में तैयार किया जा सकता है: रोगीकरण मोड में प्रजनन और मृत्यु की सबसे सरल प्रणाली के लिए, किसी भी दो आसन्न राज्यों के बीच संभाव्यता धाराएं बराबर होती हैं।
समीकरणों की परिणामी प्रणाली कम पहले के बराबर है। समीकरणों की अंतिम प्रणाली को संकलित करने के लिए, पड़ोसी राज्यों को अलग करने वाली ऊर्ध्वाधर रेखा को ले जाना आवश्यक है, और परिणामी सीमा के माध्यम से धाराओं को समान रखें।
गणितीय प्रेरण द्वारा सिस्टम (2.5) का समाधान पाया जा सकता है।
I \u003d 1 में हमारे पास है
प्राप्त समानता के प्रकार से पता चलता है कि समीकरणों की प्रणाली का समग्र समाधान (2.5) का रूप है:
या, यह देखते हुए, परिभाषा के अनुसार, एक खाली सेट पर काम एक है:
इस प्रकार, स्थिर मोड के लिए पीआई की सभी संभावनाएं केवल अज्ञात निरंतर पी 0 के माध्यम से व्यक्त की जाती हैं। समानता (2.4) एक अतिरिक्त शर्त देता है जो आपको पी 0 निर्धारित करने की अनुमति देता है। फिर, सभी पर संक्षेप में, पी 0 के लिए हम प्राप्त करते हैं (2.7):
आइए हम पीआई की स्थिर संभावनाओं के अस्तित्व के मुद्दे पर जाएं। संभावनाओं को परिभाषित करने के लिए प्राप्त अभिव्यक्तियों के लिए, आवश्यकता आमतौर पर p0\u003e 0 के लिए अतिरंजित होती है। यह स्पष्ट रूप से संबंधित समीकरणों में प्रजनन गुणांक और मृत्यु पर प्रतिबंध लगा देता है। अनिवार्य रूप से यह आवश्यक है कि सिस्टम कभी-कभी खाली होता है; यदि आप वास्तविक जीवन के उदाहरणों को चालू करते हैं तो यह स्थिरता की स्थिति बहुत उचित प्रतीत होती है। यदि यह बहुत तेजी से बढ़ता है, तो यह तब हो सकता है कि अंत बिंदु पर सकारात्मक संभावना के साथ, प्रक्रिया "एक असीमित रिमोट पॉइंट" में चरण स्थान (0.1, ...) छोड़ देगी? (जनसंख्या में व्यक्ति बहुत अधिक होंगे)। दूसरे शब्दों में, प्रक्रिया नियमित नहीं होगी, और फिर समानता (2.4) टूट जाएगी। हम निम्नलिखित दो राशियों को परिभाषित करते हैं:
प्रजनन और मृत्यु की प्रक्रिया की नियमितता के लिए, यह आवश्यक है और एस 2 \u003d के लिए पर्याप्त है।
अपने स्थिर वितरण के अस्तित्व के लिए, यह आवश्यक है और एस 1 के लिए पर्याप्त है< .
विचाराधीन प्रजनन और मृत्यु की प्रक्रिया के ईआई के सभी राज्यों के लिए, यह आवश्यक है और श्रृंखला एस 1 के अभिसरण के लिए पर्याप्त है< , при этом ряд должен расходиться S2 = . Только эргодический случай приводит к установившимся вероятностям Pi, i = 0, 1, 2, …, и именно этот случай представляет интерес. Заметим, что условия эргодичности выполняются, например, когда, начиная с некоторого i, все члены последовательности {} ограничены единицей, т. е. тогда, когда существует некоторое i0 (и некоторое С<1) такое, что для всех ii0 выполняется неравенство:
इस असमानता को एक साधारण व्याख्या दी जा सकती है: कुछ राज्य ईआई से शुरू करना और बाद के सभी राज्यों के लिए, प्रजनन की धारा की तीव्रता मृत्यु के प्रवाह की तीव्रता से कम होनी चाहिए।
कभी-कभी अभ्यास में "शुद्ध" प्रजनन की प्रक्रियाएं होती हैं। "शुद्ध" प्रजनन की प्रक्रिया मृत्यु और प्रजनन की प्रक्रिया है, जिसमें सभी मौत की प्रवाह शून्य शून्य होती है। राज्यों की संख्या को सीमित किए बिना ऐसी प्रक्रिया के राज्यों का ग्राफ आंकड़ा (2.2) में दिखाया गया है:
चित्रा 2.2 - "शुद्ध" प्रजनन की प्रक्रिया के लिए संक्रमण तीव्रता का ग्राफ
इसी प्रकार, "स्वच्छ" मौत की अवधारणा पेश की गई है। "स्वच्छ" मौत की प्रक्रिया को मौत और प्रजनन की इस तरह की प्रक्रिया कहा जाता है, जिसमें सभी प्रजनन प्रवाह की तीव्रता शून्य होती है। राज्यों की संख्या को सीमित किए बिना ऐसी प्रक्रिया के राज्यों का ग्राफ आंकड़ा में दिखाया गया है:
चित्रा 2.3 - "शुद्ध" मौत की प्रक्रिया के लिए संक्रमण तीव्रता की गिनती
ऐसी प्रक्रियाओं के लिए कोल्मोगोरोव समीकरण प्रणाली समीकरणों की प्रणाली (2.1) से प्राप्त की जा सकती है, जिसमें प्रवाह प्रक्रिया की सभी तीव्रताओं को शून्य के बराबर प्रवाह करना आवश्यक है :.
2. सरल द्रव्यमान रखरखाव प्रणाली के मामले में मौत के नुकसान के उदाहरण
मास रखरखाव प्रणाली एम / एम / 1 के लिए गणितीय अपेक्षा की 1 परिभाषा
विचाराधीन द्रव्यमान रखरखाव प्रणाली निम्नलिखित संक्रमण ग्राफ (चित्रा 3.1) के साथ प्रजनन और मृत्यु की प्रक्रिया है:
चित्रा 3.1 - एम / एम / 1 सिस्टम के लिए संक्रमण तीव्रता की गणना करें
मौत और प्रजनन की प्रक्रिया के लिए ergodicity की स्थिति से, यह इस प्रकार है कि यदि एक स्थिर वितरण है जो ergodic के साथ मेल खाता है नेटवर्क लोड अनुपात कहा जाता है। संतुलन समीकरण में वह रूप है जहां हमें लगता है कि:
संभावना सामान्यीकरण स्थिति (2.4) का उपयोग करके पाया जा सकता है, जहां से यह इस प्रकार है और इसलिए
यानी स्टेशनरी मोड में इस तरह के एक बड़े पैमाने पर रखरखाव प्रणाली में अनुप्रयोगों की संख्या एक ज्यामितीय वितरण है।
इस वितरण के उत्पादक कार्य को खोजने में आसान:
यहां से हम स्थिर मोड में सिस्टम में अनुप्रयोगों की औसत संख्या के लिए एक अभिव्यक्ति प्राप्त करते हैं:
जाहिर है, बड़े पैमाने पर सेवा प्रणाली में कतार असीमित बढ़ रही है।
मास रखरखाव प्रणाली एम / एम / एन / 0 के लिए गणितीय अपेक्षा की 2 परिभाषा
इंतजार किए बिना यह एक हानि प्रणाली है। यदि एप्लिकेशन उस समय सिस्टम में प्रवेश करता है जब सेवा सभी एन लाइनों द्वारा कब्जा कर लिया जाता है, तो यह खो जाता है। इस तरह की एक प्रणाली पिछले शताब्दी की शुरुआत में डेनिश एरलांग इंजीनियर द्वारा पेश की गई थी और टेलीफोन एक्सचेंज में प्रवेश करने वाले कॉल प्रोसेसिंग मॉडल के रूप में लागू किया गया था। इस तरह के एक बड़े रखरखाव प्रणाली के लिए संक्रमण का ग्राफ फॉर्म (चित्रा 3.2) है:
चित्रा 3.2 - एम / एम / एन / 0 सिस्टम के लिए तीव्रता तीव्रता की गणना करें
बेशक सिस्टम राज्यों की संख्या के बाद से, और मार्कोव श्रृंखला irreducible है, एकमात्र स्थिर वितरण जो एर्गोडिक के साथ मेल खाता है, हमेशा किसी भी पैरामीटर के साथ मौजूद है।
यहां से हमें मिलता है:
संभावना, हमेशा की तरह, सामान्यीकरण की स्थिति (2.4), स्थान से मिल सकती है:
इस प्रकार, हमें मिलता है:
सिस्टम में अनुप्रयोगों की औसत संख्या संबंध से निर्धारित की जाती है:
बड़े एन के साथ, आप एसिम्प्टोटिक्स का उपयोग कर सकते हैं।
2.3 मास रखरखाव प्रणाली एम / एम / एन के लिए गणितीय अपेक्षा की परिभाषा
यह उम्मीद के साथ एक बहु-केबल प्रणाली है। यदि सभी एन लाइनों को सर्विसिंग अनुप्रयोगों द्वारा कब्जा कर लिया जाता है, तो सेवा तीव्रता बराबर होती है। इस प्रणाली के लिए संक्रमण ग्राफ का एक दृश्य है (चित्र 3.3):
चित्रा 3.3 - एम / एम / एन सिस्टम के लिए संक्रमण की गिनती गिनती
स्थिर वितरण मौजूद है
समतोल समीकरण निम्नानुसार हैं:
जहां, पिछले मामले के समान, प्राप्त करें
इस मामले में सामान्यीकरण की शर्तें फॉर्म ले जाएंगी:
जहां से यह इस प्रकार है
निष्क्रिय मोड में अनुप्रयोगों की औसत संख्या बराबर है
2.4 मास रखरखाव प्रणाली एम / एम / एन / एन के लिए गणितीय अपेक्षा की परिभाषा
यह सीमित संख्या में स्थानों के साथ एक बहु-पक्षीय प्रणाली है। यह इस तथ्य से पिछले द्रव्यमान रखरखाव प्रणाली से अलग है कि इसमें केवल एन स्थान हैं। इसलिए, इस मामले में संक्रमणों का ग्राफ फॉर्म (चित्रा 3.4) है:
चित्रा 3.4 - एम / एम / एन / एन सिस्टम के लिए संक्रमण की गिनती गिनती
सिस्टम की संख्या की संख्या के बाद से, एकमात्र स्थिर वितरण हमेशा किसी भी पैरामीटर के साथ मौजूद है। संतुलन समीकरण फॉर्म लेते हैं:
जहां यह रोगी की संभावनाओं का पालन करता है, पिछले द्रव्यमान सेवा प्रणाली के लिए एक ही रूप है, केवल एक ही अंतर के साथ उन्हें परिभाषित किया गया है। इस तरह
संभावना सामान्यीकरण की शर्तों से निर्धारित की जाती है (2.4):
कहाँ मिलता है:
सिस्टम में अनुप्रयोगों की औसत संख्या संबंध से निर्धारित की जाती है:
3. प्रजनन और मृत्यु की कुछ प्रक्रियाओं के लिए गणितीय उम्मीद की परिभाषा
रैखिक रूप से बढ़ती जन्म तीव्रता और मृत्यु के साथ प्रजनन और मृत्यु की प्रक्रिया
चित्रा 1 - प्रजनन और मृत्यु की प्रक्रिया के पहले मामले के लिए संक्रमण तीव्रता का ग्राफ
हम राज्यों की स्थिर संभावनाओं के लिए समीकरण संतुलन लिखते हैं:
गणितीय अपेक्षा निर्धारित करने के लिए, हम निम्नलिखित सूत्र का उपयोग करते हैं:
सूत्र द्वारा निर्धारित किया जाता है।
इस प्रकार, निश्चित मोड में सिस्टम में अनुप्रयोगों की औसत संख्या यह है:
3.2 रैखिक रूप से बढ़ती जन्म तीव्रता और चतुर्भुज बढ़ती मौत की तीव्रता के साथ प्रजनन और मृत्यु की प्रक्रिया
स्पीड ली को, जिस वॉल्यूम की मात्रा में प्रजनन, और एमआई की मौत की तीव्रता, निर्दिष्ट गति की तीव्रता, जिस पर मृत्यु I जनसंख्या में मृत्यु होती है, निम्नलिखित नियमों द्वारा निर्धारित की जाती है:
प्रजनन और मृत्यु की इस प्रक्रिया के लिए संक्रमण तीव्रता का ग्राफ फॉर्म है:
चित्रा 2 - प्रजनन और मृत्यु की प्रक्रिया के दूसरे मामले के लिए संक्रमण तीव्रता का ग्राफ
हम राज्यों की स्थिर संभावनाओं के लिए समीकरण संतुलन लिखते हैं:
रैखिक रूप से बढ़ती जन्म तीव्रता और चतुर्भुज की बढ़ती मौत की तीव्रता के साथ प्रजनन और मृत्यु की प्रक्रिया
स्पीड ली को, जिस वॉल्यूम की मात्रा में प्रजनन, और एमआई की मौत की तीव्रता, निर्दिष्ट गति की तीव्रता, जिस पर मृत्यु I जनसंख्या में मृत्यु होती है, निम्नलिखित नियमों द्वारा निर्धारित की जाती है:
प्रजनन और मृत्यु की इस प्रक्रिया के लिए संक्रमण तीव्रता का ग्राफ फॉर्म है
चित्रा 3 - प्रजनन और मृत्यु की प्रक्रिया के तीसरे मामले के लिए संक्रमण तीव्रता की गिनती
हम राज्यों की स्थिर संभावनाओं के लिए समीकरण संतुलन लिखते हैं:
गणितीय उम्मीद खोजने के लिए, हम सूत्र का उपयोग करते हैं। हम यह प्राप्त करते हैं कि स्थिर मोड में अनुप्रयोगों की औसत संख्या यह है:
3.4 अतिरिक्त धारा और infinite उपकरणों की संख्या
स्पीड ली को, जिस वॉल्यूम की मात्रा में प्रजनन, और एमआई की मौत की तीव्रता, निर्दिष्ट गति की तीव्रता, जिस पर मृत्यु I जनसंख्या में मृत्यु होती है, निम्नलिखित नियमों द्वारा निर्धारित की जाती है:
प्रजनन और मृत्यु की इस प्रक्रिया के लिए संक्रमण तीव्रता का ग्राफ फॉर्म है:
चित्रा 4 - प्रजनन और मृत्यु की प्रक्रिया के चौथे मामले के लिए संक्रमण तीव्रता का ग्राफ
हम राज्यों की स्थिर संभावनाओं के लिए समीकरण संतुलन लिखते हैं:
गणितीय उम्मीद खोजने के लिए, हम सूत्र का उपयोग करते हैं। हम यह प्राप्त करते हैं कि स्थिर मोड में अनुप्रयोगों की औसत संख्या यह है:
ऊपर से एक अनुमान बनाओ:
तौर पर:
एक आवेदन रहने के समय के लिए 3.5 प्रणाली
स्पीड ली को, जिस वॉल्यूम की मात्रा में प्रजनन, और एमआई की मौत की तीव्रता, निर्दिष्ट गति की तीव्रता, जिस पर मृत्यु I जनसंख्या में मृत्यु होती है, निम्नलिखित नियमों द्वारा निर्धारित की जाती है:
प्रजनन और मृत्यु की इस प्रक्रिया के लिए संक्रमण तीव्रता का ग्राफ फॉर्म है:
चित्रा 5 - प्रजनन और मृत्यु की प्रक्रिया के पांचवें मामले के लिए संक्रमण तीव्रता का ग्राफ
हम राज्यों की स्थिर संभावनाओं के लिए समीकरण संतुलन लिखते हैं:
गणितीय उम्मीद खोजने के लिए, हम सूत्र का उपयोग करते हैं। हम यह प्राप्त करते हैं कि स्थिर मोड में अनुप्रयोगों की औसत संख्या यह है:
ऊपर से एक अनुमान बनाओ:
तौर पर:
हमें स्थिर मोड में सिस्टम में अनुप्रयोगों की औसत संख्या के लिए निम्न रेटिंग मिलती है:
3.6 सिस्टम रहने के समय के लिए प्रतिबंध के साथ सिस्टम, अतिरिक्त धारा और उपकरणों की अनंत संख्या
स्पीड ली, जिसके साथ वॉल्यूम की मात्रा का प्रचार, और एमआई की मौत की तीव्रता, निर्दिष्ट गति के साथ निर्दिष्ट गति के साथ मृत्यु उत्पन्न होती है, पाठ नियम पर निर्धारित होती है:
प्रजनन और मृत्यु की इस प्रक्रिया के लिए संक्रमण तीव्रता का ग्राफ फॉर्म है:
चित्रा 6 - प्रजनन और मृत्यु की प्रक्रिया के छठे मामले के लिए संक्रमण तीव्रता की गिनती
हम राज्यों की स्थिर संभावनाओं के लिए समीकरण संतुलन लिखते हैं:
गणितीय उम्मीद खोजने के लिए, हम सूत्र का उपयोग करते हैं। हम यह प्राप्त करते हैं कि स्थिर मोड में अनुप्रयोगों की औसत संख्या यह है:
ऊपर से एक अनुमान बनाओ:
तौर पर:
हमें स्थिर मोड में सिस्टम में अनुप्रयोगों की औसत संख्या के लिए निम्न रेटिंग मिलती है:
निष्कर्ष
इसलिए, हमने प्रजनन और मृत्यु की प्रक्रिया के सार और गणितीय मॉडल को देखा और इसके आधार पर - चार मूलभूत प्रकार के द्रव्यमान सेवा प्रणालियों के मॉडल: नुकसान और अपेक्षाओं के साथ। निर्धारित किया गया है कि निरंतर समय के साथ प्रजनन और मृत्यु की मार्कोव प्रक्रिया को ऐसी यादृच्छिक प्रक्रिया कहा जाता है जो कई गैर-नकारात्मक मान ले सकता है; जिनमें से कोई भी समय नहीं हो सकता है, जबकि किसी भी समय यह या तो एक द्वारा बढ़ सकता है, या एक से कम हो सकता है या अपरिवर्तित रहता है।
इसके अलावा इस पेपर में, सैद्धांतिक प्रमाणपत्र और विभिन्न प्रजनन और मृत्यु प्रक्रियाओं के लिए गणितीय अपेक्षाओं के निर्धारण के उदाहरण प्रस्तुत किए गए थे, व्यावहारिक कार्यों का समाधान किया गया था।
इस प्रकार, प्रजनन और मृत्यु प्रक्रियाओं की मदद से, विभिन्न प्रक्रियाओं के नियंत्रण के गणितीय मॉडल, साथ ही जीवविज्ञान, भौतिकी और अन्य क्षेत्रों में कई घटनाओं के मॉडल भी। इसके अलावा, विभिन्न तकनीकी प्रणालियों के अध्ययन में इंजीनियरिंग अभ्यास में मृत्यु और प्रजनन प्रक्रियाओं का व्यापक रूप से उपयोग किया जाता है, पर्यावरण में होने वाली कई प्रक्रियाओं का सीधा संबंध है। मार्कोव प्रक्रियाएं बड़े पैमाने पर सेवा के सिद्धांत को रेखांकित करती हैं, जो बदले में अर्थव्यवस्था में अनिवार्य है, विशेष रूप से जब उद्यम और विभिन्न प्रक्रियाओं में होने वाली विभिन्न प्रक्रियाओं का प्रबंधन किया जाता है।
इस पेपर में, प्रजनन और मृत्यु की प्रक्रियाओं को सीमा संभावनाओं की गणना के लिए मानी जाती है और सूत्रों का उपयोग किया जाता है, जिसका उपयोग बड़े पैमाने पर रखरखाव प्रणाली का वर्णन करने के लिए किया जाता है ताकि अनुप्रयोगों के सबसे सरल प्रवाह के आधार पर नुकसान और अपेक्षाओं के साथ। कुछ विशेषताओं के लिए सूत्र प्राप्त किए जाते हैं।
प्रयुक्त स्रोतों की सूची
वेंटसेल, ई.एस. यादृच्छिक प्रक्रियाओं और इसके इंजीनियरिंग अनुप्रयोगों का सिद्धांत: छात्र ट्यूटोरियल / ई.एस. वेंटसेल, एलए। Ovcharov - दूसरा एड। - एम।: "हायर स्कूल", 2000. - 384 पी।
Malinkovsky, yu.v. बड़े पैमाने पर सेवा के सिद्धांत पर व्याख्यान: विश्वविद्यालयों / YU.V के लिए ट्यूटोरियल। Malinkovsky। - गोमेल: जीएसयू उन्हें। एफ स्कीरिना, - 184 पी। (इलेक्ट्रॉनिक संस्करण)
बरुचा रीड, एटी। मार्कोव प्रक्रियाओं और उनके अनुप्रयोगों / एटी के सिद्धांत के तत्व। Barucha_rid - एम।: विज्ञान, 1 9 6 9. - 512 पी।
सेवसायनोव, बीए। कुछ प्रकार के मार्कोव प्रक्रियाओं / बीए पर। SevastyAnov - टी। 4, वॉल्यूम। 4 - उमन, 1 9 4 9. - के साथ। 194।
कोल्मोगोरोव, एएन। संभावनाओं के सिद्धांत का परिचय: अध्ययन। विश्वविद्यालयों / आई.जी. के लिए Zhurbenko, A.V. प्रोकोरोव - एम।: विज्ञान, 1 9 82. - 160 एस।
ट्यूशन
भाषा विषयों का अध्ययन करने में मदद की ज़रूरत है?
हमारे विशेषज्ञ ब्याज के विषय के लिए शिक्षण सेवाओं की सलाह देंगे या हैं।
एक अनुरोध भेजें परामर्श प्राप्त करने की संभावना के बारे में जानने के लिए अभी विषय के साथ।
इस सैद्धांतिक कार्य में, निरंतर मार्कोव चेन की योजना पर विचार किया जाएगा - तथाकथित "decitity और प्रजनन योजना"
यह विषय आर्थिक, पर्यावरणीय और जैविक प्रक्रियाओं के अध्ययन में मार्कोव प्रक्रियाओं के उच्च महत्व के कारण बेहद प्रासंगिक है, इसके अलावा, मार्कोव प्रक्रियाएं जन सेवा के सिद्धांत के केंद्र में हैं, जो वर्तमान में विभिन्न आर्थिक क्षेत्रों में सक्रिय रूप से उपयोग की जाती हैं, उद्यम में प्रक्रियाओं के प्रबंधन सहित।
मौत और प्रजनन की मार्कोव प्रक्रियाओं का व्यापक रूप से बायोस्फीयर, पारिस्थितिक तंत्र आदि में होने वाली विभिन्न प्रक्रियाओं को समझाने में उपयोग किया जाता है। यह ध्यान दिया जाना चाहिए कि इस प्रकार की मार्कोव प्रक्रियाओं को जीवविज्ञान में व्यापक उपयोग के कारण, विशेष रूप से अलग-अलग आबादी के पुनरुत्पादन को अनुकरण करने के कारण इसका नाम प्राप्त हुआ।
इस पेपर में, समस्या और प्रजनन की प्रक्रियाओं का उपयोग समस्या को हल करने में किया जाएगा, जिसका उद्देश्य अलग-अलग आबादी में मधुमक्खियों की अनुमानित राशि मिलनी है।
सैद्धांतिक भाग
सैद्धांतिक भाग के हिस्से के रूप में, सीमा संभावनाओं के लिए बीजगणितीय समीकरण लिखे जाएंगे। जाहिर है, यदि मार्कोव की दो निरंतर श्रृंखलाओं के पास एक ही राज्य ग्राफ होता है और केवल तीव्रता मूल्यों में भिन्न होता है,
आप तुरंत प्रत्येक ग्राफ के लिए राज्यों की सीमा संभावनाओं को तुरंत ढूंढ सकते हैं, यह उनमें से एक के लिए समीकरण के पत्र में संकलित और हल करने के लिए पर्याप्त है, और फिर संबंधित मानों के बजाय प्रतिस्थापित करें। ग्राफ के कई सामान्य आंकड़ों के लिए, एक पत्र में रैखिक समीकरण आसानी से हल हो जाते हैं।
इस पेपर में, निरंतर मार्कोव चेन की योजना का वर्णन किया जाएगा - तथाकथित "मृत्यु और प्रजनन का आरेख"।
मार्कोव निरंतर श्रृंखला को "मृत्यु और प्रजनन की प्रक्रिया" कहा जाता है, यदि राज्यों के ग्राफ में अंजीर में प्रस्तुत उपस्थिति होती है। 1.1, यानी सभी राज्यों को एक श्रृंखला में खींचा जा सकता है जिसमें प्रत्येक औसत राज्य (एस 2, ..., एस एन -1) प्रत्येक आस-पास के राज्यों और चरम राज्यों के साथ सीधे और प्रतिक्रिया के साथ जुड़ा हुआ है ( एस 1, एस एन) - केवल एक पड़ोसी राज्य के साथ।
राज्यों की सीमा संभावनाओं के लिए बीजगणितीय समीकरणों को रिकॉर्ड करने के लिए, किसी प्रकार का कार्य करें।
उदाहरण। तकनीकी उपकरण में तीन समान नोड होते हैं; उनमें से प्रत्येक असफल हो सकता है (मना कर दिया); अस्वीकृत नोड तुरंत ठीक होने लगता है। दोषपूर्ण नोड्स की संख्या द्वारा सिस्टम राज्य संख्या:
एस 0 - सभी तीन नोड्स अच्छे हैं;
एस 1 - एक नोड ने इनकार कर दिया (बहाल), दो अच्छे हैं;
एस 2 - दो नोड्स बहाल किए गए हैं, एक काम कर रहा है;
एस 3 - सभी तीन नोड्स बहाल किए गए हैं।
गिनती राज्य अंजीर में दिखाए जाते हैं। 1.2। ग्राफ से यह स्पष्ट है कि सिस्टम में बहने वाली प्रक्रिया "मौत और प्रजनन" की प्रक्रिया है।
![]()
मौत और प्रजनन की योजना अक्सर व्यावहारिक कार्यों की एक विस्तृत विविधता में पाया जाता है; इसलिए, यह सामान्य रूप से इस योजना पर विचार करने और बीजगणितीय समीकरणों की इसी प्रणाली को हल करने के लिए पहले से ही समझ में आता है ताकि भविष्य में, ऐसी योजना के अनुसार होने वाली विशिष्ट प्रक्रियाओं के साथ मिलकर, हर बार समस्या को फिर से हल न करें, लेकिन उपयोग करने के लिए तैयार समाधान।
तो, अंजीर में दिखाए गए राज्यों के ग्राफ के साथ मौत और प्रजनन की यादृच्छिक प्रक्रिया पर विचार करें। 1.3।

हम राज्यों की संभावनाओं के लिए बीजगणितीय समीकरण लिखेंगे। पहले राज्य के लिए हमारे पास है:
एस 2 की दूसरी स्थिति के लिए, आने वाले और आउटगोइंग तीरों के अनुरूप सदस्यों की मात्रा के बराबर हैं:
लेकिन, (1.2) के आधार पर, आप सही कटौती कर सकते हैं और एक दूसरे के सदस्यों के बराबर छोड़ सकते हैं और प्राप्त कर सकते हैं:
एक शब्द में, मृत्यु और प्रजनन की योजना के लिए, एक दूसरे के ऊपर खड़े तीर के अनुरूप सदस्य एक दूसरे के बराबर होते हैं:
कहा पे क। 2 से सभी मान लेता है एन
तो, राज्यों की सीमा संभावनाएं आर के पी 2\u003e ..., आर पी इन मृत्यु और प्रजनन का कोई भी आरेख समीकरणों को संतुष्ट करता है:
 (1.4)
(1.4)
और सामान्यीकरण की स्थिति:
![]() (1.5)
(1.5)
हम इस प्रणाली को निम्नानुसार हल करेंगे: पहले समीकरण (1.4) एक्सप्रेस से पी 2:
दूसरे से, ध्यान में रखते हुए (1.6), हमें मिलता है
 (1.7)
(1.7)
तीसरे से, ध्यान में रखते हुए (1.7):

 (1.8)
(1.8)
यह सूत्र किसी के लिए मान्य है क। 2 से पी
इसकी संरचना पर ध्यान दें। संख्यात्मक में बाएं से दाएं द्वारा निर्देशित तीरों द्वारा खड़े संक्रमण (तीव्रता) की संभावना की सभी घनत्व का एक उत्पाद है, शुरुआत से ही एक राज्य में जाता है जो एक राज्य में जाता है एस के। ; संप्रदाय में - सभी तीव्रता का काम , तीरों द्वारा खड़े होकर दाएं बाएं जा रहे हैं, फिर से, शुरुआत से और राज्य से बाहर जाने वाले तीर तक एस के। । के लिये k \u003d n. तीव्रता की संख्या संख्या में खड़ी होगी , बाएं दाएं जाने वाले सभी तीरों के साथ खड़े होकर, और denominator में - सभी तीर दाहिने ओर जा रहे हैं।
तो, सभी संभावनाएं उनमें से एक के माध्यम से व्यक्त की जाती हैं :. सामान्यीकरण स्थिति में इन अभिव्यक्तियों को प्रतिस्थापित करें: ![]() । हम पाते हैं:
। हम पाते हैं:
शेष संभावनाओं के माध्यम से व्यक्त किया जाता है
 (1.10)
(1.10)
इस प्रकार, सामान्य रूप में "मृत्यु और प्रजनन" का कार्य हल किया जाता है: राज्यों की सीमा संभावनाएं पाए जाते हैं।
व्यावहारिक भाग
मार्कोव प्रक्रियाओं, विशेष रूप से मृत्यु और प्रजनन में, काम का वर्णन करने और सिस्टम की एक विस्तृत वर्ग का विश्लेषण करने के लिए उपयोग की जाती है जो किसी भी कारण से दूसरे स्थानों से दूसरे स्थान पर दोहराए गए संक्रमण होते हैं। ऐसे सिस्टम में, वे यादृच्छिक रूप से होते हैं, जब कुछ घटनाएं होती हैं (घटना प्रवाह) होती हैं तो एक मनमानी पल के दौरान हो गई। एक नियम के रूप में, वे दो प्रकार हैं: उनमें से एक को पारंपरिक रूप से वस्तु का जन्म कहा जाता है, और दूसरा उसकी मृत्यु है।
बीईई परिवारों का प्राकृतिक प्रजनन - वर्तमान समय में सिस्टम में बहने वाली प्रक्रियाओं के दृष्टिकोण से, एक संभावित प्रक्रिया के रूप में विचार करना संभव है जब परिवार एक निश्चित बिंदु पर परिवार काम करने वाले राज्य से रोह में जा सकता है । विभिन्न कारकों के आधार पर, नियंत्रित तकनीकी और कमजोर नियंत्रित जैविक और जलवायु दोनों, यह परिवार को एक काम करने की स्थिति में समाप्त या वापस कर सकता है। साथ ही, परिवार बार-बार एक चीज़ पर स्विच कर सकता है, फिर दूसरे राज्य में। इस प्रकार, प्रक्रिया के गणितीय मॉडल का वर्णन करने के लिए, सजातीय मार्कोव प्रक्रियाओं के सिद्धांत को लागू करने की अनुमति है।
रूह राज्य में मधुमक्खी परिवार के संक्रमण की तीव्रता प्रजनन है - बड़े पैमाने पर युवा कमजोर मधुमक्खियों के संचय की दर से निर्धारित है। रिवर्स ट्रांज़िशन की तीव्रता "मौत" है - परिवार की वापसी काम करने की स्थिति में, जो बदले में, वास्तविक अवधि, टूटने का चयन और मधुमक्खियों (दूतों का गठन), अमृत की मात्रा पर निर्भर करता है एकत्र, आदि
रोथ राज्य में परिवार के मधुमक्खी के संक्रमण की संभावना सबसे पहले इसे जारी करने वाली प्रक्रियाओं की तीव्रता से निर्धारित की जाएगी, और एंटी-टेस्टर्स μ, जो कम करने के लिए उपयोग की जाने वाली तकनीकों पर निर्भर करती है। परिवारों का मार्ग। नतीजतन, चर्चा की गई प्रक्रियाओं को प्रभावित करने के लिए, प्रवाह λ और μ (चित्र 1) की तीव्रता और दिशा को बदलने के लिए आवश्यक है।

मधुमक्खियों का एकल चयन मॉडलिंग हिस्सा (उनकी "मौत" में वृद्धि) से पता चला कि कार्यशील राज्य की घटना की संभावना स्थगर्शी रूप से है, और गुलाबी की संभावना को स्थगित कर दिया गया है। विरोधी होने वाली जगह में - 5-7 हजार मधुमक्खियों (दो या तीन मानक फ्रेम) के परिवार से चयन - रोसियम की संभावना 0.05 होगी, और काम करने की स्थिति की संभावना 0.8 है; मधुमक्खियों के साथ तीन फ्रेम से अधिक का चयन बहुत कम राशि की संभावना को कम कर देता है।
हम मधुमक्खियों में रॉडिंग की प्रक्रिया से संबंधित व्यावहारिक कार्य को हल करेंगे।
शुरुआत के लिए, हम चित्रा 1 में ग्राफ के समान एक ग्राफ का निर्माण करते हैं, संक्रमण की तीव्रता या किसी अन्य स्थिति में संक्रमण के साथ।
| |
|
